Observation of Doppler shift ${\mathit{f}}_{\mathbf{D}}$ modulated by the internal kink mode using conventional reflectometry in the EAST tokamak

1.   Introduction

Microwave reflectometry has been proven to be a powerful diagnostic tool with excellent spatial and temporal resolution for measuring electron density profiles and fluctuations, rotation velocity and so on [1]. Over the past few decades, various types of reflectometers have been developed in almost all fusion devices; these can be grouped into two categories depending on the diagnostic setup and detected signals [2, 3]. One category is conventional reflectometers, which probe the plasma perpendicularly to the density cutoff surfaces and detect the reflected signal from the cutoff layer. Here, the received turbulence spectrum exhibits a symmetric character, and this technique has been well developed for measuring the electron density profile, density fluctuation and plasma instabilities [4]. The other category is Doppler reflectometers, which launch the probing wave at a finite tilt angle relative to the cutoff layer normal and measure the Bragg backscattered signals at the cutoff layer. This setup induces a Doppler shift ${f}_{\mathrm{D}}$ on the measured turbulence spectrum. By analyzing this Doppler shift, Doppler reflectometry can measure perpendicular rotation velocity, radial electric field and its shear, etc [4].

As a type of conventional reflectometry, W-band poloidal correlation reflectometry (PCR) has been performed successfully since 2018 and has become a key diagnostic tool for measuring electron density fluctuation in the plasma core of the EAST tokamak [5]. This paper presents an experimental observation on the turbulence spectrum measured by the PCR system, which exhibits asymmetry and an induced Doppler shift ${f}_{\mathrm{D}}$ during the phase of internal kink mode (IKM) rotation. This Doppler shift is the target measurement of Doppler reflectometry, but captured in this case by conventional reflectometry. Moreover, we find that the Doppler shift is periodically modulated by the changes in the effective angle between the probing wave and cutoff layer normal, but not by the plasma turbulence.

IKMs, such as the fishbone mode and saturated long-lived mode (LLM) with a mode number of m/n = 1/1, are frequently observed in neutral beam injection (NBI)-heated plasma in the EAST tokamak, and their presence greatly affects plasma performance [6‒10]. It has been observed in EAST that a field-line-localized small-scale density fluctuation is destabilized due to an m/n = 1/1 IKM [11]. Therefore, study of the characteristics of IKMs and their effect on turbulence could be beneficial for understanding the related plasma physics. The remaining sections of this paper are arranged as follows. Section 2 gives a description of the diagnostics for analysis, section 3 presents the experimental observations and section 4 provides the simulation results to verify the experimental observations. Finally, section 5 offers a discussion and summary.

2.   Diagnostics for analysis

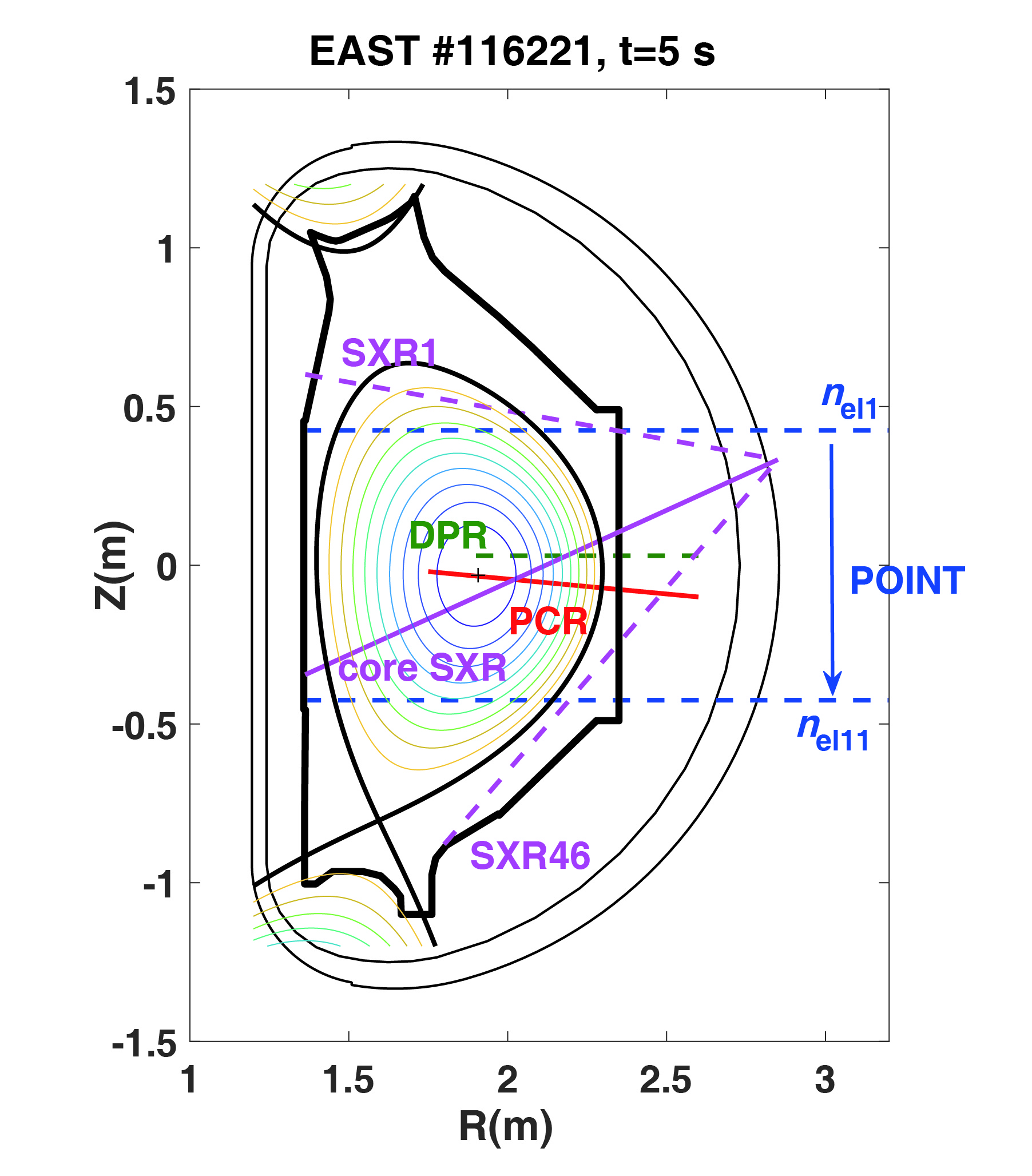
The experiment is carried out on the EAST tokamak, a medium-sized flexible divertor configuration tokamak with major radius R₀ = 1.85 m and minor radius α = 0.45 m. The main diagnostics used for analysis are shown in figure 1. The 46-channel soft x-ray (SXR) imaging system has been used to study the large-scale core magnetohydrodynamic phenomena in EAST [12]. One core channel SXR is chosen to confirm the position and intensity of the IKMs. The electron density profile is obtained based on a density profile reconstruction method combining a POINT (polarimeter/interferometer) and a fast-sweeping density profile reflectometer (DPR) [13]. The POINT has 11 channels uniformly distributed from top to bottom in the same poloidal cross-section. The DPR is located at the low-field side and has a horizontal view about 3 cm above the midplane.

Figure  1.  Poloidal views of the diagnostics used for analysis.

DownLoad: Full-Size Img PowerPoint

The W-band PCR diagnostic system is utilized to measure core density fluctuation in the EAST tokamak. The antenna array of the W-band PCR is about 16 cm below the midplane at the low-field side of EAST, as shown in figure 1. Four fixed probing frequencies (79.2, 85.2, 91.8 and 96 GHz) are launched into the plasma simultaneously using the same launching antenna A with an inclined view, and the reflected waves are received through two adjacent antennas B and C with a poloidal separation of 5 cm, as shown in figure 2 [5]. PCR adopts I/Q detection technology and can measure in-phase (I) and quadrature (Q) signals. A complex signal (S) can be constructed as $S=I+\mathrm{i}Q$. PCR has a sampling frequency of 2 MHz, and thus can measure fluctuating components with a frequency of up to 1 MHz. The center of gravity (COG) of the complex amplitude spectrum, also called the weighted mean, is introduced to extract the Doppler shift ${f}_{\mathrm{D}}$ from the PCR signals. First, a fast Fourier transform (FFT) is applied to the PCR signal to obtain a double-sided power spectrum $S\left(f\right)$. Then, a simple weighted spectrum yields ${f}_{\mathrm{D}}=\sum f\cdot\dfrac{S\left(f\right)}{\sum S\left(f\right)}$. Finally, the time sequences of ${f}_{\mathrm{D}}\left(t\right)$ can be obtained by sliding the FFT through the time signal [14]. In this paper, the four frequencies of the W-band PCR will be named PCR1, PCR2, PCR3 and PCR4, and the corresponding Doppler shifts will be labeled ${f}_{\mathrm{D}1}$, ${f}_{\mathrm{D}2}$, ${f}_{\mathrm{D}3}$ and ${f}_{\mathrm{D}4}$, respectively.

Figure  2.  Antenna arrangement of W-band PCR system. A is the launching antenna and B and C are receiving antennas.

DownLoad: Full-Size Img PowerPoint

3.   Experimental observation

3.1   The Doppler shift f_D is modulated by the IKM

The characteristics of IKMs and their induced fluctuations were investigated in a series of NBI-heated plasmas in EAST. A typical discharge is presented in figure 3. Some of the main plasma parameters are as follows: toroidal magnetic field (B_T) = 1.64 T, plasma current I_p = 420 kA, central line-averaged plasma density from POINT n_e = (3–4.5) × 10¹⁹ m⁻³, NBI heating power P_NBI = 3.8 MW, low hybrid wave (LHW) heating power P_LHW = 1 MW and a lower signal null (LSN) divertor configuration. The NBI system in EAST has four wave sources that are step-by-step injected into the plasma. The plasma enters H-mode at about t = 2.6 s. Shortly after the third NBI ion source is injected, the fishbone mode is observed from the core SXR signal. When the fourth ion source is injected, the fishbone mode is sustained and the amplitude of the fishbone gradually increases. From t = 3.5 s, the electron density is evaluated gradually by gas puffing, as shown in figure 3(a).

Figure  3.  Typical discharge #116221: (a) line-averaged electron density, (b) D_α signal in the lower divertor, (c) core SXR signal, (d) LHW and NBI heating power.

DownLoad: Full-Size Img PowerPoint

Figures 4(a)–(e) show the signals of the core SXR and Doppler shift ${f}_{\mathrm{D}}$ extracted from the four channels of the PCR. Figures 4(f)–(j) present their time–frequency spectrums. From figure 4(f), the fishbone mode frequency (~20 kHz) can always be observed on the core SXR signal until the fishbone mode disappears at t = 5.65 s. However, fishbone mode frequency is not observed on the spectrogram of ${f}_{\mathrm{D}1}$, but is found on the spectrogram of ${f}_{\mathrm{D}2}$, ${f}_{\mathrm{D}3}$ and ${f}_{\mathrm{D}4}$ in different sequences. The fishbone frequency is first observed in the spectrum of ${f}_{\mathrm{D}2}$ at t = 3.56 s and maintained until t = 5.4 s, followed by ${f}_{\mathrm{D}3}$ at t = 4.35–5.5 s and finally ${f}_{\mathrm{D}4}$ at t = 4.99–5.53 s. Here the validation of PCR measurement must be discussed. For X-mode polarization, the cutoff positions of PCR are determined by the magnetic field and electron density. Figure 5 shows a calculated example of the PCR cutoff position. Magnetic field distribution is assumed based on the 1/R dependence of B_T. Figure 5(a) is the electron density profile given by combining POINT and DPR diagnostic data. Figure 5(b) shows two characteristic plasma frequencies on the equatorial plane: the dotted brown line represents the second harmonic of the electron cyclotron emission (ECE) frequency (${f}_{2*\mathrm{c}\mathrm{e}}$) and the solid black line is the right-hand cutoff frequency (${f}_{\mathrm{R}}$). The probing wave of the PCR system is launched into the plasma from the low-field side, and its cutoff can be found at the place where the probing frequency equals the local right-hand cutoff frequency (${f}_{\mathrm{R}}$). When the probing wave frequency is equal to the second harmonic of ECE frequency (${f}_{2*\mathrm{c}\mathrm{e}}$), the probing wave can be absorbed by the plasma. At t = 5 s, the PCR1 signal is absorbed by the plasma and PCR2, PCR3 and PCR4 work well with the cutoff located at $\rho$ = 0.26, $\rho$ = 0.15 and $\rho$ = 0.05, respectively, as shown in figure 5. Here, $\rho$ is the normalized toroidal flux coordinate.

Figure  4.  Core SXR signal and Doppler shift ${f}_{\mathrm{D}}$ extracted from the four channels of the PCR and their time–frequency spectra.

DownLoad: Full-Size Img PowerPoint

Figure  5.  Calculation example of PCR cutoff positions: (a) electron density profile and (b) two characteristic plasma frequencies and cutoff locations of PCR channels.

DownLoad: Full-Size Img PowerPoint

As shown in figure 6(a), the location of the fishbone mode near $\rho$ = 0.28 is almost unchanged. Cross-correlation analysis is conducted to demonstrate the relationship between the fishbone mode and PCR signals. A definition of the coefficient γ can be found in reference [15]. The spectrograms of coherence value (γ) at the fishbone mode frequency between the Doppler shift ${f}_{\mathrm{D}}$ of each PCR channel and the core SXR signal are shown in figures 5(b)–(e). Before t = 3.5 s, γ is lower than the noise level and the fishbone frequency is not observed in the time–frequency spectrum of any of the four PCR channels. Owing to the low plasma electron density at this time, the probing waves of PCR1 and PCR2 are absorbed by the plasma and those of PCR3 and PCR4 pass through the plasma. From t = 3.5 s, the cutoff position of the PCRs gradually moves toward the plasma core as the electron density is slowly elevated by gas puffing. When the PCR cutoff (${\rho }_{\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{f}}$) is inside the location of the fishbone mode (${\rho }_{\mathrm{f}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{e}}$), the value of the correlation coefficient γ becomes higher than the noise level and the fishbone frequency can be observed clearly on the spectrum of the Doppler shift ${f}_{\mathrm{D}}$. This finding indicates that the PCR signal is modulated by the fishbone mode. For example, at t = 5.5 s, the cutoff positions of PCR1 and PCR2 are both outside the location of the fishbone mode, and the fishbone mode frequency cannot be seen in figures 6(b) and (c). However, at this time, both PCR3 and PCR4 are located inside the fishbone mode position, and the fishbone mode frequency can be clearly observed on the spectra of ${f}_{\mathrm{D}3}$ and ${f}_{\mathrm{D}4}$, as shown in figures 6(d) and (e). Therefore, we can conclude that when the cutoff of PCR is inside the fishbone mode position (${\rho }_{\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{f}} < {\rho }_{\mathrm{f}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{e}})$, the Doppler shift ${f}_{\mathrm{D}}$ can be modulated by the fishbone mode.

Figure  6.  (a) Cutoff positions of four PCR channels and the location of the fishbone mode. Solid circles representing fishbone mode frequency can be observed on the spectrum of this channel; hollow circles indicate that no fishbone mode frequency is observed; and no indication in the figure indicates that the probing frequency passes through the plasma. (b)–(e) Spectrogram of coherence value (γ) at the fishbone mode frequency between the core SXR signal and Doppler shift ${f}_{\mathrm{D}}$ of each PCR channel.

DownLoad: Full-Size Img PowerPoint

Figure 7 shows the spectrograms of fluctuation measured by PCR3 and the evolution of Doppler shift ${f}_{\mathrm{D}}$ calculated by the COG method during one full fishbone mode cycle. Figure 7(b) shows that the PCR3 spectrogram exhibits broadband fluctuation with frequency within ±500 kHz just before the kink mode (t = 5.1366–5.1369 s), and the positive and negative frequency components are symmetrical. However, during the phase of IKM rotation (t = 5.1369–5.139 s), the fluctuation enhancement appears intermittently, especially for the high-frequency components (500–950 kHz and −950 to −500 kHz). Moreover, the evolution of ${f}_{\mathrm{D}}$ is consistent with the oscillation on the core SXR signal. These findings are evident from the enlarged views in figures 7(c) and (d). Given that the spectrum of PCR3 in figures 7(b) and (e) is obtained based on limited data points (a window length of 32 data points), the information reflected by this spectrum may not be accurate enough. This speculation can be further proved by the evolution of the integrated power of positive frequency components ${S}_{\left[0-950\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ (red line) and negative frequency components ${S}_{\left[-950-0\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ (blue) measured by PCR3 as shown in figure 6(e). ${S}_{\left[0-950\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ and ${S}_{\left[-950-0\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ are periodically suppressed and recovered during the phase of IKM rotation. When ${S}_{\left[0-950\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ is ‘suppressed’ or ‘recovered’ during the modulation, a corresponding ‘increase’ or ‘decrease’ occurs in ${S}_{\left[-950-0\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ and the value of Doppler shift ${f}_{\mathrm{D}}$ becomes ‘negative’ or ‘positive’.

Figure  7.  (a) Core SXR signal showing one full fishbone mode cycle. The oscillation on the signal is due to the IKM rotation. (b) Spectrograms of fluctuation measured by PCR3 with a window length of 32 data points. The black dotted line represents the Doppler shift ${f}_{\mathrm{D}}$ calculated by the COG method. (c)–(e) Enlargements of the time window of 5.1379–5.1383 s in (a) and (b). (e) Integrated power of positive frequency components ${S}_{\left[0-950\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ (red line) and negative frequency components ${S}_{\left[-950-0\right]\mathrm{k}\mathrm{H}\mathrm{z}}$ (blue) measured by PCR3.

DownLoad: Full-Size Img PowerPoint

The above observation will be explained through the diagnostic principle of the PCR system. As mentioned in section 1, the probing waves of the PCR are launched into the plasma with an incident angle of ~10° to ensure that they are perpendicular to the cutoff layer. The incident angle is fixed on the EAST tokamak and thus should be related to the change in the cutoff layer due to IKM rotation. If the probing wave is launched to the cutoff layer at an oblique angle, then the received signal from the plasma is not from reflection but from Bragg backscattering. If the fluctuating plasma moves, then the scattered wave will exhibit a Doppler shift and the shifted frequency ${f}_{\mathrm{D}}$ can be defined as follows:

where $\overrightarrow{u}$ is the turbulence velocity, and $\overrightarrow{k}$ is the turbulence wavenumber. Both can be decomposed into poloidal (${k}_{\perp }$, ${u}_{\perp }$), toroidal (${k}_{\parallel }$, ${u}_{\parallel }$) and radial (${k}_{r}$, ${u}_{r}$) directions. For typical density fluctuations in tokamak plasma, ${{k}_{\perp }\gg k}_{\parallel }$ and ${k}_{r}{u}_{r}\sim 0$. Therefore, the Doppler shift frequency can be given as follows:

The wavenumber of fluctuation matches the Bragg condition ${k}_{\perp }={2k}_{0}\mathrm{s}\mathrm{i}\mathrm{n}\theta$ near the cutoff layer based on the slab model. Here, ${k}_{0}$ is the wavenumber of the probing wave in a vacuum and $\theta$ means the effective angle between the probing wave and cutoff layer normal. Thus

As can be seen from figure 7, during t = 5.1366–5.1369 s, ${f}_{\mathrm{D}}$ changes a little with an amplitude of less than 100 kHz; however, later, during t = 5.1379‒5.1383 s, it reaches a maximum value of 500 kHz; which means that IKM rotation can increase the value of the f_D by a factor of five within one fishbone mode cycle. From the equation above, ${f}_{\mathrm{D}}$ is determined by the perpendicular velocity (${u}_{\perp }$) and the effective angle $\theta$. In this discharge, the heating power is constant during t = 3.5‒6 s, so the perpendicular velocity cannot change significantly. Therefore, the change in ${f}_{\mathrm{D}}$ is mainly related to the effective angle $\theta$ rather than the perpendicular velocity. Figure 8 is schematic representation of the modulation of the effective angle $\theta$ between the probing wave (black line) and plasma cutoff layer normal (blue dotted line). IKM rotation will change the shape of cutoff layer, thus changing the effective angle $\theta$.

Figure  8.  Schematic representation of the modulation of the effective angle $\theta$ between the probing wave (black line) and plasma cutoff layer normal (blue dotted line).

DownLoad: Full-Size Img PowerPoint

3.2   Dependence of Doppler shift f_D on IKM amplitude

The fishbone mode and saturated LLM are typical IKMs. Two discharges, #116221 with the fishbone mode and #94070 with LLM, are chosen to explore the relationship between kink mode amplitude and Doppler shift ${f}_{\mathrm{D}}$. As displayed in figure 9, the top panels show the wavelet of the core SXR signal, and the fishbone mode and LLM can be observed clearly. The original core SXR signals are shown in figures 9(b) and (e), and their envelopes are presented (marked as a red solid line) and used to indicate the amplitude of the kink mode. Here, the envelopes are calculated by using root-mean-square (RMS) levels. Figures 9(c) and (f) reveal the evolution of ${f}_{\mathrm{D}}$ from PCR3 and present the envelopes of positive (red line) and negative (blue line) frequency components. According to these findings, ${f}_{\mathrm{D}}$ is modulated by the kink mode and the value of ${f}_{\mathrm{D}}$ is highly correlated with the kink mode amplitude. Figure 10 shows the results of statistical analysis from the envelopes of the original SXR signal and ${f}_{\mathrm{D}}$. The value of ${|f}_{\mathrm{D}}|$ increases with the kink mode amplitude. However, no threshold of kink mode amplitude exists in the stimulation of ${f}_{\mathrm{D}}$. These indicate that even a small-amplitude IKM has an effect on the effective angle, and the influence of the effective angle increases with the IKM amplitude.

Figure  9.  Evolution of Doppler shift ${f}_{\mathrm{D}}$ with kink mode rotation for the fishbone mode case (#116221) and LLM case (#94070). (a), (d) Wavelets of core SXR signals. (b), (e) Original signal of core SXR with envelopes (red line). (c), (f) The Doppler shift ${f}_{\mathrm{D}}$ from PCR3 with the envelopes of positive frequency components (red line) and negative frequency components (blue line).

DownLoad: Full-Size Img PowerPoint

Figure  10.  Dependence of Doppler shift ${f}_{\mathrm{D}}$ on the kink mode amplitude (A_{kink mode}). The oblique dashed lines indicate that ${|f}_{\mathrm{D}}|$ is positively correlated with A_{kink mode}.

DownLoad: Full-Size Img PowerPoint

The envelopes of positive and negative frequency components look symmetric for the fishbone case in discharge #116221 but asymmetric for the LLM case in discharge #94070, as shown in figures 9(c) and (f). The value of ${|f}_{\mathrm{D}}|$ from the positive frequency component is close to that from the negative frequency component at the same kink mode amplitude for the fishbone case in figure 10(a). However, the value of ${|f}_{\mathrm{D}}|$ from the positive frequency component is greater than that from the negative frequency components at the same kink mode amplitude for the LLM case in figure 10(b). This phenomenon may be related to the plasma configuration. Given that the antenna horn of the PCR system is located below the middle plane, discharge #116221 is an LSN divertor configuration and discharge #94070 is an upper signal null (USN) divertor configuration. Therefore, the effect of kink mode rotation on the angle between the probing wave and cutoff layer normal becomes different, as eventually reflected in the symmetry of positive and negative frequency components of ${f}_{\mathrm{D}}$.

4.   Simulated results

Simulation analysis is conducted to verify the above experimental observation. A one-dimensional (1D) electron density profile with core density perturbation is assumed and then mapped to the two-dimensional (2D) plasma configuration in EAST. The typical density profile on EAST can be seen as a composite of a steep pedestal gradient region and a tilted core region, as shown on the left axis of figure 11. The modulation of core density perturbation is used to simulate the effect of IKM rotation. In the analysis, core density perturbation $\delta {n}_{\mathrm{e}}$ is assumed as follows：

Figure  11.  The assumed density profile (left-hand axis) and the density perturbation $\delta {n}_{\mathrm{e}}$ (right-hand axis).

DownLoad: Full-Size Img PowerPoint

where ${\varPsi }_{\mathrm{p}}$ is the normalized poloidal flux coordinate. This core density perturbation is localized inside ${\varPsi }_{\mathrm{p}}=0.3,$ as shown on the right axis of figure 11. The modulation of density distribution can then be obtained by mapping onto the 2D plasma configuration as follows:

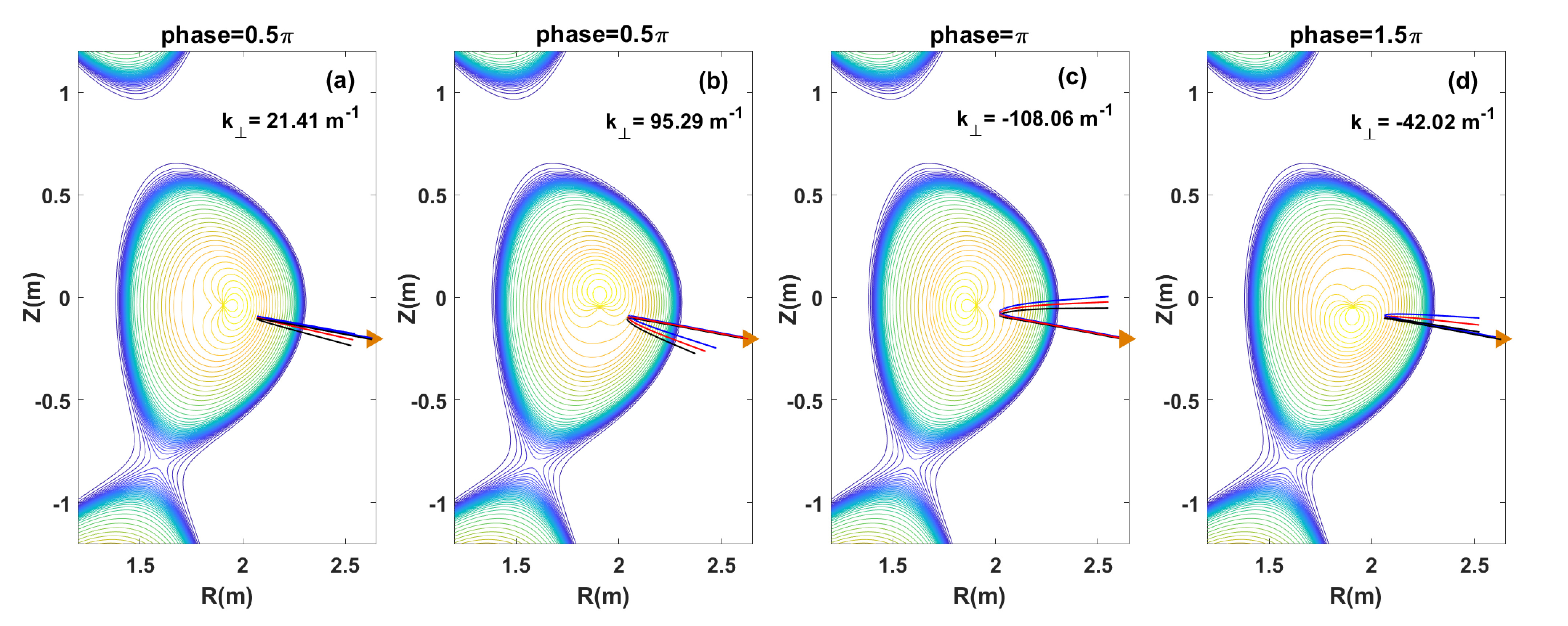
where ${n}_{\mathrm{e}}$ and $\delta {n}_{\mathrm{e}}$ are defined in figure 11, $\alpha$ is the poloidal angle of the coordinate point in real space, m is the poloidal mode number of density perturbation and $\varphi$ is the phase. For the simulation of m/n = 1/1 IKM rotation, m is set to 1. Different values of $\varphi$ indicate rotation to different poloidal positions; for example, the variation of $\varphi$ from 0 to 2${\text{π}}$ represents one cycle of core density perturbation rotation. Then, 91.8 GHz is chosen as the probing wave frequency. For the tokamak configuration, the slab model is inappropriate and a ray-tracing calculation is necessary. As presented in equation (3), the perpendicular wavenumber (${k}_{\perp })$ at the cutoff position, which contains the information on $\mathrm{sin}\;\theta$, can be directly derived based on a ray-tracing method considering the diffraction effect [16, 17]. In this calculation, the incident wave is assumed to be Gaussian. Three rays are launched into plasma; the central ray (the red line) indicates the launching beam and two additional rays (blue and black) are launched defining the boundary of the Gaussian beam, as shown in figures 12 and 13. Finally, the evolution of perpendicular wavenumber (${k}_{\perp })$ with the core density perturbation rotation can be achieved to represent the effective angle $\theta$.

Figure  12.  Assumed density profile mapped to the plasma shape of discharge #116221 with the LSN configuration. Parts (a)–(d) show the situations when the rotation phase is 0, $0.5 {\text{π}}$, 1${\text{π}}$ and $1.5{\text{π}}$, respectively. The brown line is the incident probing waves, the black curve is the cutoff layer, and the blue dotted line is the cutoff layer normal.

DownLoad: Full-Size Img PowerPoint

Figure  13.  Assumed density profile mapped to the plasma shape of discharge #94070 with the USN configuration. Parts (a)–(d) show the situations when the rotation phase is 0, $0.5{\text{π}}$, 1${\text{π}}$ and $1.5{\text{π}}$, respectively.

DownLoad: Full-Size Img PowerPoint

Figure 14 presents the simulated results of ray-tracing calculations for the two cases: the blue circles are the raw data of the perpendicular wavenumber (${k}_{\perp })$ and the red lines are the fitted curves. Both show that the perpendicular wavenumber (${k}_{\perp })$ evolves as a sine function with core density perturbation rotation. Figure 14(a) is the result obtained by mapping the assumed 1D density profile onto the 2D plasma shape of discharge #116221 with LSN configuration. In one cycle of core density perturbation rotation the positive and negative parts of ${k}_{\perp }$ are almost symmetrical, each occupying half a cycle, and the amplitude of the positive part is approximately equal to that of the negative part. This finding is consistent with the experimental observations in figures 10(a). Figure 12 shows the rotation phase at 0, $0.5{\text{π}}$, 1${\text{π}}$ and $1.5{\text{π}}$. The brown triangle represents the launching antenna. Figure 14(b) shows the result obtained by mapping the assumed 1D density profile onto the 2D plasma shape of discharge #94070 with USN configuration. The positive and negative parts of ${k}_{\perp }$ are not symmetrical. In one cycle of core density perturbation rotation, the positive part takes a longer time and has a greater amplitude than the negative part. This result is also consistent with the experimental observations in figure 10(b). Details can be found in figure 13.

Figure  14.  The perpendicular wavenumber (${k}_{\perp })$evolving with the density perturbation rotation. (a) Case for discharge #116221 with the LSN configuration. (b) Case for discharge #94070 with the USN configuration.

DownLoad: Full-Size Img PowerPoint

These simulated results reveal that the rotation of core density perturbation affects the shape of the cutoff layer and thus changes the effective angle $\theta$ between the probing wave and cutoff layer normal. Moreover, the plasma configuration (LSN or USN) has an influence on the symmetry of the ${f}_{\mathrm{D}}$ value. These simulation results are consistent with the experimental observations in section 3, indicating that the Doppler shift ${f}_{\mathrm{D}}$ from a PCR-measured signal is modulated by the IKM due to the changes in the effective angle $\theta$ between the probing wave and cutoff layer normal.

5.   Discussion and summary

We have presented evidence in section 4 that the IKM modulates the Doppler shift ${f}_{\mathrm{D}}$ by changing the effective angle $\theta$. Here, we discuss two important questions. One is the utility of this finding; this mechanism can be utilized to study the local characteristics of the IKM at different radial positions by launching continuous probe frequencies, thereby obtaining values for ${f}_{\mathrm{D}}$ at different radial cutoff positions. Thus, this method can complement the commonly used line-integrated measurements of soft x-rays. Regarding the second question, it is not certain whether this modulation phenomenon can affect profile reflectometry measurements. Currently, the reflectometer systems for density profile measurements on the EAST tokamak are composed of Q-band (32–56 GHz), V-band (48–76 GHz) and W-band (72–110 GHz) reflectometers [18]. The cutoff position of the W-band system is mainly in the plasma core; thus, the impact of this modulation phenomenon on these frequencies needs to be evaluated, and a correction method must be found for the probable existing error. Besides, as mentioned above, the Doppler shift ${f}_{\mathrm{D}}$ affected by the IKM is due to the changes in effective angle between the probing wave and cutoff layer normal and not plasma turbulence. Therefore, to study the behavior of plasma turbulence induced by the IKM, strategies to minimize or eliminate this effect on the PCR measurements must be further explored.

In summary, we present experimental observations and simulations on how the IKM modulates the Doppler shift ${f}_{\mathrm{D}}$, which is extracted from the measured signal spectra using a conventional reflectometry technique, poloidal correlation reflectometry (PCR), on the EAST tokamak. The underlying reason is that the IKM rotation periodically changes the effective angle between the probing wave and cutoff layer normal. When the cutoff position of the probing wave is located within the kink mode position, this phenomenon can be captured by the PCR system. Moreover, the value of the Doppler shift ${f}_{\mathrm{D}}$ is positively correlated with the amplitude of the kink mode, even when the latter is small. The plasma configuration (USN or LSN) affects the symmetry of the positive and negative frequency components of the Doppler shift ${f}_{\mathrm{D}}$. These results establish a clear link between the Doppler shift and IKM. We believe that the results will be helpful for investigating the characteristics of the IKM and related physical phenomena.