Tamping the movement of the laser absorption cutoff position using gold foam hohlraum

1.   Introduction

In laser indirect-driven inertial confinement fusion (ICF) experiments, laser energy is delivered to a hohlraum and converted to X-rays [1], which drive the capsule to implode. Notably, researchers at Lawrence Livermore National Laboratory recently achieved 3.88 MJ of fusion energy using 2.05 MJ of laser energy [2], marking a 20% increase from the December 2022 shot that yielded 3.15 MJ of fusion energy [3]. The subsequent objective is to attain an even higher fusion yield, underscoring the critical importance of further enhancing the hohlraum performance and symmetry [4–6]. In the ICF hohlraum, plasma blowing off from the hohlraum wall influences the radiation symmetry. As plasma blows off the wall, both the laser absorption layer and the X-ray reemission zone shift away from the wall. This changes the angle between the source and the capsule for a fixed pointing direction [7]. Maintaining the laser spot in proximity to the original wall facilitates more accessible symmetry control [8].

There are many approaches to tamping the motion of the laser absorption layer. A low-Z liner on the gold hohlraum, which blows off to fill the hohlraum interior with low-Z plasma, was rejected because of the pressure created on the axis by the stagnation of the liner [7]. Using a low-Z foam-filled hohlraum [9] may cause too many X-rays to be preheated in the capsule. An initial low-Z gas-filled hohlraum [10, 11] of pure He at a density of 0.96 mg cm⁻³ was chosen [12] because it can reduce laser plasma instability (LPI) [13] effects and improve symmetry. However, these high-gas-fill hohlraum designs had problems with strong time-dependent asymmetries. The classical Rayleigh-Taylor (RT) instability occurs at the interface of gas and plasma blowoff [14], as well as significant stimulated Raman scattering (SRS) [15]. As a result, a lower gas-filled hohlraum with 0.3–0.45 g cm⁻³ He is used at present [17]. Recently, a hollow-walled hohlraum (I-Raum) was designed to reduce the growth of the gold bubble and stabilize the gold–gas interface [18]. Experimental results showed that the implosion core has been more prolate for the I-Raum compared to the cylinder hohlraum [19].

Another way to improve the hohlraum performance is the utilization of a low-density, high-Z foam hohlraum [20–23]. This approach not only yields higher radiation temperatures due to reduced X-ray energy loss in the hohlraum wall [24–26], but also results in less plasma blowoff [27]. Low-density high-Z foam shows unique advantages in improving the hohlraum performance. Experimental results indicate that the X-ray emission fronts moving away from the wall were considerably smaller for 0.3 g cm⁻³ gold foam compared to 19.3 g cm⁻³ solid gold [27]. Experiments involving hohlraums lined with a 20 mg cm⁻³ 400 μm thick Ta₂O₅ aerogel showed an improvement in the capsule performance, but a measurable increase in backscatter [28], a phenomenon suppressed in the solid Ta₂O₅-lined hohlraum [29]. It is imperative to investigate the hohlraum performance across various foam densities. However, the density dependence of foam on mitigating the motion of the laser absorption layer in a laser-driven hohlraum remains unresolved.

In this study, we examine the motion of laser spots with varying wall densities, considering both short square laser pulses and long-shaped laser pulses. Here, we simplify the laser-hohlraum interaction to the 1D cylindrical geometry problem, where the laser is vertically incident from the axis onto the gold hohlraum wall. We investigate the influence of the initial wall density on the movement of the laser absorption cutoff position. Simulations are performed using the 1D Lagrangian radiation hydrodynamics code MULTI [30]. The motion of the laser spot is characterized by the laser absorption cutoff position, representing the point where 1% of the laser energy remains. Simulation results reveal that foam gold can effectively mitigate the motion of the laser absorption cutoff position. Optimal densities differ for various laser pulses in minimizing the motion of the laser absorption cutoff position. For the short square laser pulse, the optimal density is 0.6 g cm⁻³, whereas for long-shaped laser pulses, it is 0.1 g cm⁻³.

2.   Simulation results and discussion

The optimal choice of the ratio of the hohlraum radius to the capsule radius is strongly influenced by the need to achieve a higher hohlraum temperature and a very high degree of flux uniformity on the capsule [7]. A larger ratio is very effective at smoothing all but the longest-wavelength perturbations. However, an increased hohlraum radius diminishes the hohlraum coupling efficiency. If the laser absorption cutoff position shifts toward the center, mimicking a reduction in the hohlraum radius, the coupling efficiency improves but the symmetry deteriorates. Concurrently, the wall plasma blocks the inner beams from reaching the hohlraum [31] and leads to low mode asymmetry. Maintaining the ratio of the initial hohlraum radius to the capsule radius is crucial by curbing the motion of the laser absorption cutoff position induced by wall plasma blowoff. To enhance the hohlraum symmetry without losing coupling efficiency, low-density gold foam has been used in the ICF hohlraum.

An experimental study on the expanding plasma movement of low-density gold foam (~1% solid density) irradiated by a high-power laser was conducted using an SG-III prototype laser [27]. Compared to solid gold with a density of 19.3 g cm⁻³, the velocities of X-ray emission fronts moving off the wall are much smaller for gold foam with a density of 0.3 g cm⁻³. The density of Au foam decreases uniformly after heating, resulting in diminished movement of soft X-ray and M-band emission fronts. These results indicate that the foam wall may have less plasma fill and X-ray emission front movement. Theoretical analysis and MULTI 1D simulation results corroborate these observations, indicating lower plasma blowoff velocities and smaller density contour movement velocities for gold foam compared to solid gold. However, the foam density in this experiment is suboptimal for hohlraum symmetry, and the performance of gold foam under the ignition pulse condition remains unexplored. This study delves into the foam density dependence for mitigating the motion of the laser absorption cutoff position in a laser-driven hohlraum through simulations.

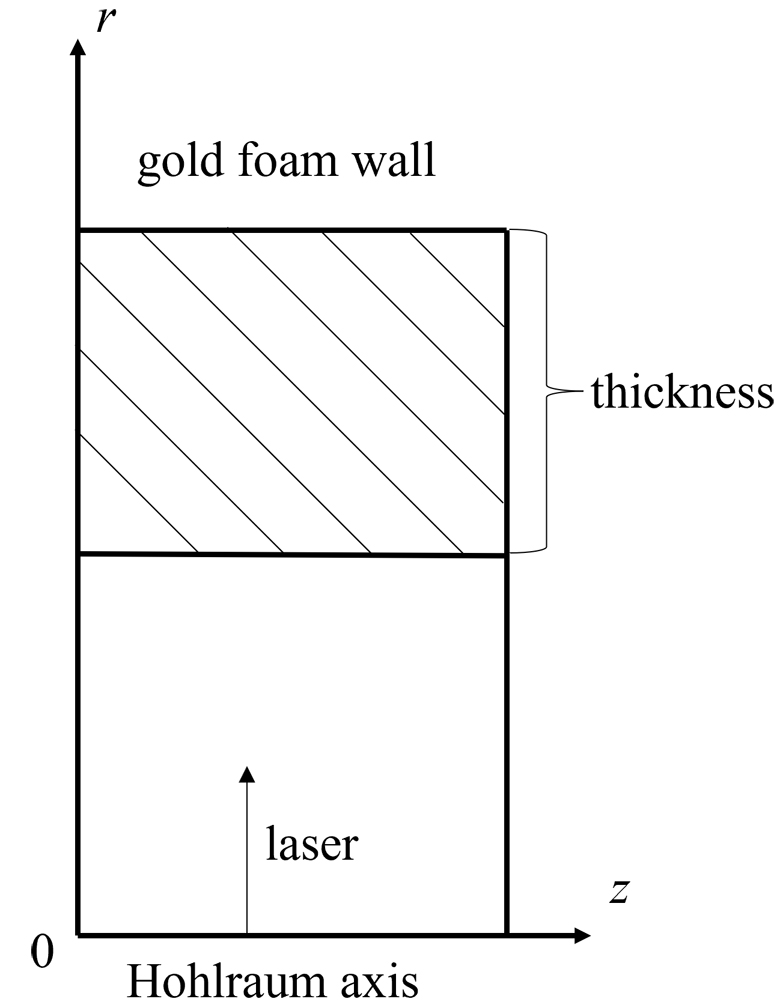
In a 1D cylindrical geometry, we assume a uniform laser heating of the wall from the axis, with consistent effects along the axis, as depicted in figure 1. Our simulations, aimed at evaluating the feasibility of employing low-density foam in an ignition hohlraum, adopt the hohlraum radius and incident laser power parameters based on the National Ignition Facility (NIF) ignition target [7]. The hohlraum radius r is 2.75 mm, and the wall thickness with solid gold is 30 μm. For the low-density foam, the wall thickness is adjusted to maintain an areal density equivalent to that of the solid wall. Here, the absorption position motion for two laser pulses is studied: the short square laser pulse and the long-shaped laser pulse. The power of the short square laser pulse aligns with the peak power of the NIF ignition pulse, as the laser energy deposited in the wall is mainly determined by the peak power of the ignition pulse. The long-shaped laser pulse is the NIF ignition pulse, providing insights for guiding the design of the hohlraum wall density.

Figure  1.  Schematic of the 1D cylindrical geometry simulation. The wall areal density remains the same by increasing the thickness of the low-foam wall.

DownLoad: Full-Size Img PowerPoint

The laser power is in J (s cm)⁻¹ units. The opacity of Au is given by SNOP [32], and the equation of state comes from the SESAME library. The flux limiter f is set as 0.08.

2.1   Short square laser pulse

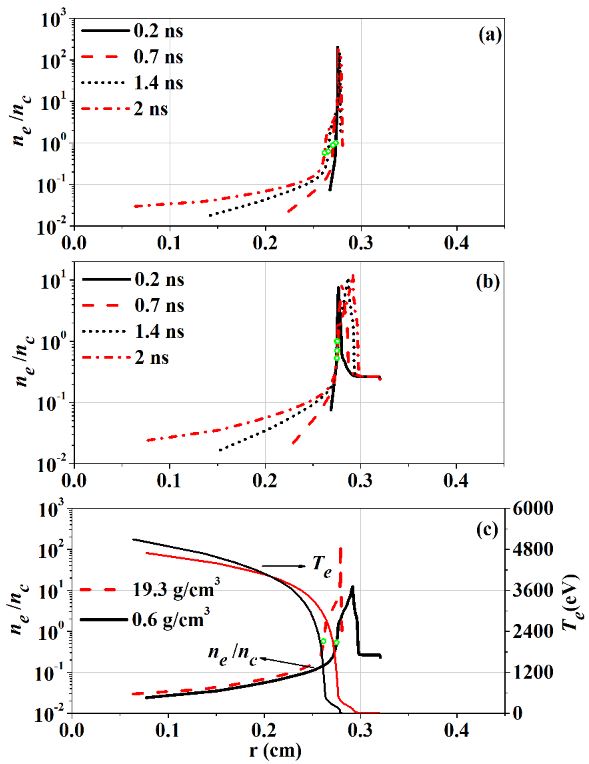
A short square laser pulse has a 2 ns pulse with 0.351 μm wavelength. The peak power is P_L, and the laser linear power in 1D cylindrical geometry is P_L×2πr = 3.35×10¹⁴ W cm⁻¹, with a hohlraum radius of 2.75 mm. Plasma blowing off from the wall absorbs the laser energy. The absorption cutoff position is referred to as r_lacp. Figure 2 shows the motion of r_lacp with time. When the initial density is lower than 0.6 g cm⁻³, r_lacp moves into the wall with time, and r_lacp remains almost unchanged at the density of 0.6 g cm⁻³, shown as the red-dotted line in figure 2. However, r_lacp moves off the wall when the wall’s initial density is higher than 0.6 g cm⁻³.

Figure  2.  Motion of the laser absorption cutoff position r_lacp for several wall densities in the short-pulse condition. 0.3 g cm⁻³: solid line; 0.5 g cm⁻³: dashed line; 0.6 g cm⁻³: dotted line; 2 g cm⁻³: dot-dashed line; 19.3 g cm⁻³: solid line with diamond markers.

DownLoad: Full-Size Img PowerPoint

The spatial distributions of electron density with initial densities of 19.3 g cm⁻³ and 0.6 g cm⁻³ are shown in figure 3, where r_lacp is denoted by green hollow spots. The electron density at the absorption cutoff position is defined as n_{e_lacp}. When the laser irradiates the hohlraum wall, the plasma moves from the wall toward the hohlraum axis. The electron density distributions are self-similar with the time increasing. The critical density n_c is about 8.9×10²¹ cm⁻³ for a laser with λ = 0.351 μm. In figure 3(a), for the solid Au case, the absorption cutoff position moves toward the center, causing n_{e_lacp} to decrease over time. At 2 ns, the laser absorption cutoff position moves by about 130 μm, and n_{e_lacp} is reduced from the critical density to ~0.57n_c. In figure 3(b), for the 0.6 g cm⁻³ foam gold case, n_{e_lacp} decreases from the critical density to ~0.53n_c at 2 ns, but the laser absorption cutoff position is almost unchanged.

Figure  3.  Typical electron density and temperature distribution under short square laser pulse conditions. The absorption cutoff positions are marked with green hollow spots. (a) Electron density spatial distribution of initial density 19.3 g cm⁻³. (b) Electron density spatial distribution of initial density 0.6 g cm⁻³. (c) Comparison of electron density and temperature spatial distribution between solid gold and 0.6 g cm⁻³ foam gold at 2 ns.

DownLoad: Full-Size Img PowerPoint

The laser intensity follows ${I}_{\mathrm{L}}\propto \mathrm{e}\mathrm{x}\mathrm{p}(-Kx)$ when propagating in plasma, where K is the absorption coefficient and K $\propto$ n_e³ [33]. x is the absorption length. As the plasma expands over time, the absorption length x increases, leading to a decrease in the coefficient K and, consequently, a decline in n_{e_lacp}. For the 0.6 g cm⁻³ foam gold case, the absorption length x precisely corresponds to the plasma expanding distance, resulting in a decrease in n_{e_lacp}, while the laser absorption cutoff position remains stationary.

Figure 3(c) shows the electron density and temperature distribution for solid gold and 0.6 g cm⁻³ foam gold at 2 ns. The laser absorption cutoff position is defined as r_lacp, and the density at this position is denoted as ρ_lacp. The laser absorption typically occurs when r < r_lacp, and the energy transporting into the wall up to the laser ablative wavefront is mainly carried by electron conduction [33]. The heated material can be divided into the corona, conduction zone and shocked material. The density distribution depends on the rarefaction wave after the ablative front. A double-rarefaction model is proposed to describe the approximate density profile [27]. It satisfies $\rho (x,t) = {\rho _0}{\left[\dfrac{2}{{\gamma + 1}} + \dfrac{{\gamma - 1}}{{\gamma + 1}}\dfrac{x}{{{c_0}t}}\right]^{2/(\gamma - 1)}}$ for the conduction zone (rarefaction 1) and the corona (rarefaction 2). In the conduction zone, the initial densities ρ₀ correspond to the shocked material densities, while in the corona, the coefficient ρ₀ is equivalent to ρ_lacp.

As shown in figure 3(c), the ablative heat wavefront of the 0.6 g cm⁻³ foam gold is closer to the initial wall compared to solid gold. This is caused by the disparity of the ablative heat wave speed, which satisfies ${V_f} \propto 1/{\rho ^{1.03}}$ [24]. The heat wave in low-density matter propagates faster and travels further into the wall at the same time. The density distribution in the conduction zone follows the density formula. The initial densities ρ₀ differ for solid gold and 0.6 g cm⁻³ foam gold. However, the distinction between the constant γ and c₀ can be ignored for the solid and foam gold, resulting in a similar density distribution.

In the corona, based on the density formula, for the solid gold and the 0.6 g cm⁻³ foam gold, the initial density ρ₀ = ρ_lacp, resulting in a comparable spatial density distribution with r < r_lacp. In figure 3(c), the electron temperature T_e exhibits similarity in both density cases with r < r_lacp, and the electron density n_e has the same distribution as the density ρ. The n_e distributions with r < r_lacp are similar too. Consequently, despite variations in the initial wall density, the laser traverses similar plasma states. Initially, n_{e_lacp} = n_c. Over time, the plasma expands toward the center, and due to the analogous density distribution, the laser–plasma interaction remains almost identical across various initial wall density scenarios. Thus, the electron density distributions in the conduction zone and the corona are analogous with different initial wall densities. The ablative heat wavefront at a lower wall density is closer to the initial wall, as is the rarefaction front in the corona. Consequently, r_lacp is also closer to the hohlraum wall for a lower-density foam gold.

The implosion symmetry retains the original design when r_lacp remains unchanged, which can maintain a better implosion symmetry performance. Considering the symmetry and coupling efficiency, keeping r_lacp at the original position is the optimal choice. An initial density of 0.6 g cm⁻³ should be chosen for the 2 ns square laser condition in our simulation.

2.2   Long-shaped laser pulse

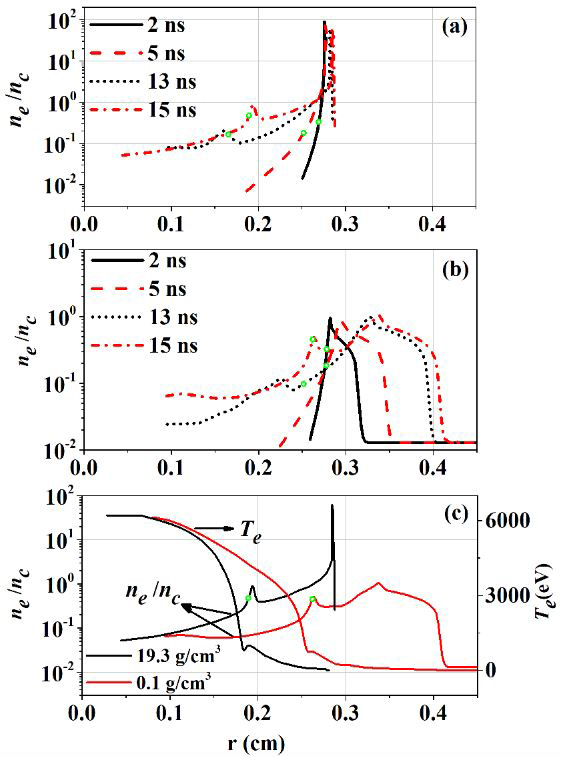
The dynamic compression driven by high-power beam pulses leads to strong shock waves. The gas dynamics show that the compression across a shock front is limited, typically to factors 4–6. To attain a higher deuterium-tritium (DT) fuel density, nearly isentropic compression is essential. Fast and nearly isentropic compression, however, can be achieved by superimposing a sequence of shocks. Each shock in the sequence has a speed larger than its predecessor and will therefore catch it up after a certain time. In ICF, the required time-shaped driving pressure is generated by appropriately time-shaping the pulse of the drive beam, as shown in figure 4, designed for the NIF ignition target [7]. This laser pulse is delivered to the hohlraum and heats the wall. Figure 5 illustrates the motions of the laser absorption cutoff position for cases with various initial wall densities and those with a gas-filled solid hohlraum. The absorption cutoff position moves to the center before ~13 ns and turns back later. This motion is influenced by the increasing input laser intensity, requiring a longer distance for laser energy absorption. At the density of 0.3 g cm⁻³, the distance between the wall and the absorption cutoff position is approximately half that at 19.3 g cm⁻³, indicating that a low-density wall effectively restrains the motion of the absorption cutoff position in the shaped pulse condition. The movement of the gas-filled solid hohlraum is illustrated by the solid line with diamond markers. Compared with the low-density lines, it moves further before ~10.6 ns during lower laser intensity duration and then returns. Before 8 ns, the gas-filled solid hohlraum with 0.3 mg cm⁻³ He is almost identical to the solid gold hohlraum. Between 8 ns and 11.8 ns, the laser absorption cutoff position under the gas-filled case is even further away from the hohlraum wall. This is mainly because the 0.3 mg cm⁻³ gas inhibits the expansion of rare low-density plasmas in the coronal region to the axis. When the gas pressure is balanced with the rare Au plasma pressure, it will cause the Au plasma density to accumulate. So, the laser cannot travel further distances. After ~13 ns, the distance between the wall and the absorption cutoff position is close to that at the density of 2 g cm⁻³. According to the above analysis, a low-density wall may be better than a gas-filled hohlraum for restraining plasma expansion. The optimal foam density is 0.1 g cm⁻³, ensuring optimal symmetry and coupling efficiency during the laser pulse.

Figure  4.  The long-shaped laser pulse used in simulation.

DownLoad: Full-Size Img PowerPoint

Figure  5.  Motion of the laser absorption cutoff position for several wall densities in the long-shaped pulse condition. 0.1 g cm⁻³: dot-dot-dashed line; 0.3 g cm⁻³: dotted line; 0.5 g cm⁻³: dashed line; 2 g cm⁻³: dot-dashed line; 19.3 g cm⁻³: solid line; gas-filled solid hohlraum with 0.3 mg cm⁻³ He: solid line with diamond markers.

DownLoad: Full-Size Img PowerPoint

Figures 6(a) and (b) present the spatial distribution of electron density at various times for initial densities of 19.3 g cm⁻³ and 0.1 g cm⁻³, respectively. Notably, the plasma expands slower in the case of 0.1 g cm⁻³ foam gold compared to 19.3 g cm⁻³ solid gold. In figure 6(a), plasma blows off from the hohlraum wall, and then the blowoff is damped at r ≈ 0.16, forming a density spike. The laser absorption cutoff position is marked with a solid dot on the spike, which is heated to expand. The density of plasma fill is higher at 15 ns than at 13 ns, and the spike moves toward the wall. Despite the increasing laser intensity leading to a rise in the laser absorption length, the absorption cutoff position remains on the spike. Initially moving toward the axis, it later shifts back toward the wall. The expanding of plasma blowoff and the motion patterns of the absorption cutoff position in figure 6(b) mirror those in figure 6(a). However, in figure 6(b), the density spike appears smoother, and the absorption cutoff position is situated near the wall. This positioning offers an advantage for symmetry control.

Figure  6.  Typical electron density and temperature distribution under long-shaped laser pulse conditions. The absorption cutoff positions are marked with green hollow spots. (a) Electron density spatial distribution of initial density 19.3 g cm⁻³. (b) Electron density spatial distribution of initial density 0.1 g cm⁻³. (c) Comparison of electron density and temperature spatial distribution between solid gold and 0.1 g cm⁻³ foam at 15 ns.

DownLoad: Full-Size Img PowerPoint

The density and temperature profiles for initial densities of 19.3 g cm⁻³ and 0.1 g cm⁻³ under the long-pulse condition exhibit self-similarity, akin to the ablation heat wave propagation observed under short-pulse conditions. In figure 6(c), the density profile of the expansion toward the axis appears almost identical. Consequently, the electron density at the laser absorption cutoff position remains consistent. Under the condition of the shaped pulse, the hohlraum wall density of the laser absorption cutoff position can be kept lower.

3.   Conclusion

In this study, we conducted simulations involving two scenarios of laser pulse interactions with a foam gold hohlraum wall. The results show that a low-density foam gold wall can restrain the movement of the laser absorption cutoff position. Due to the expansion of the heated plasma, the electron density at the laser absorption cutoff position remains below the critical density n_c, diminishing further with the increased plasma expansion. In the case of the low-density wall, the expansion of the heated plasma is slowed down. The optimal initial density for the short square laser pulse is about 0.6 g cm⁻³. The laser absorption cutoff position's motion for the long-shaped laser pulse is minimal when the initial density is about 0.1 g cm⁻³. The results show that the wall density can be optimized in different laser conditions. A low-density foam gold wall could be another way to restrain the motion of the laser absorption cutoff position for symmetry control. A foam gold hohlraum with a density of ~0.3 g cm⁻³ could be prepared. With the development of foam Au fabrication [34], the engineering application of foam Au is possible. In the future, more precise research needs to consider the natural interaction of the laser and hohlraum, including three-dimensional effects, laser oblique incidence, the foam structure [37] and other issues, which will be further incorporated.

Acknowledgments

This work was supported by the Presidential Foundation of China Academy of Engineering Physics (No. YZJJLX2018011) and National Natural Science Foundation of China (Nos. 11775204, 11734013, 12105269 and 12004351).

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.