Impact of the mass isotope on plasma confinement and transport properties in the HL-2A tokamak

1.   Introduction

The influence of the isotope mass on plasma confinement properties has been a longstanding issue in magnetically confined plasmas. According to gyro-Bohm scaling [1, 2], the plasma transport diffusivity scales as ${\rho }_{\mathrm{i}}^2{\omega }_{*}\propto {\rho }_{\mathrm{i}}^2{k}_{\perp }{V}_{*}\propto m_{\mathrm{i}}^{0.5}$ (ρ_i, ω_*, V_*, and k_⊥ represent the ion Larmor radius, diamagnetic drift frequency, diamagnetic drift velocity and perpendicular wavenumber of turbulence, respectively). Therefore, it is expected that the plasma confinement should be degraded with increasing ion mass m_i. However, in the past decades, there have been a significant amount of experiments showing strong deviations from the gyro-Bohm expectation in both tokamaks [3–12] and stellarators [13–16] under comparable hydrogen (H) and deuterium (D) discharge conditions. Meanwhile, theoretical and numerical efforts [17–26] have been made to unveil the physical mechanisms behind the isotope effects, among which the possible impact by isotopic mass on shear flow rates [25] and zonal flows [17, 23, 24] has been proposed.

The first experimental observation in the TEXTOR tokamak has demonstrated that the amplitude of geodesic acoustic mode (GAM) zonal flows substantially increases during the transition from H to D dominated plasmas [9], which is qualitatively consistent with the GKV simulation [17]. However, up to date, there has been little evidence showing the increase of nonlinear interplay between ambient turbulence and zonal flows in heavier mass isotope plasmas.

In this paper, we present direct experimental evidence to expose the fact that in D majority plasmas, the nonlinear energy transfer plays a dominant role in exciting larger GAM zonal flows by extracting more energy from ambient turbulence, which results in lower turbulent transport and better confinement compared to H majority plasmas. The results provide additional proof for understanding the isotope effects in fusion plasmas.

2.   Experimental setup

The experiments were carried out in the Ohmically-heated H and D plasmas at the HL-2A tokamak with a limiter configuration. The major and minor radii are R = 165 cm and a = 40 cm, respectively, line-averaged plasma density ${\overline{n}}_{\mathrm{e}}=1.3\times {10}^{19}{\mathrm{m}}^{-3}$, plasma current I_p = 150 kA and toroidal magnetic field B_T = 1.3 T. In the present experiments, the D (H) content was about 25% (75%) in the 'H-dominant' plasma and 70% (30%) in the 'D-dominant' plasma, respectively. To measure the edge plasma parameters and their fluctuations, a two-step Langmuir probe holder radially separated by 0.3 cm was installed at the outer midplane (low-field side) of the torus. On each step of the holder, a four-pin probe array was equipped in the triple probe model to measure the local equilibrium electron temperature T_e, density n_e and floating potential V_f [27]. The radial electric field E_r is hence deduced from the radial derivative of the plasma potential V_p = V_f + αT_e, where α is chosen to be 2.5 and 2.8 for H and D plasmas [28], respectively. The turbulent particle flux Γ_r is computed from the fluctuating density (ñ_e) and poloidal electric field (Ẽ_θ) by Γ_r=〈ñ_eẼ_θ〉/B_T in H and D dominant plasmas, where the brackets denote an ensemble average. Here, ñ_e is estimated from the ion saturation current fluctuations (${\tilde{I}}_{\mathrm{s}}$) and electron temperature fluctuations (${\tilde{T}}_{\mathrm{e}}$) detected by the triple probe with ${\tilde{n}}_{\mathrm{e}}/n_{\mathrm{e}}={\tilde{I}}_{\mathrm{s}}/I_{\mathrm{s}}-0.5{\tilde{T}}_{\mathrm{e}}/T_{\mathrm{e}}$ [29], and ${\tilde{E}}_{\theta }$ is calculated from the floating potential fluctuation difference measured on two probe pins poloidally separated by 0.4 cm. The turbulence-driven energy flux Q_r is calculated by $Q_{\mathrm{r}}=3/2(T_{\mathrm{e}}·{\mathrm{\Gamma }}_{\mathrm{r}}+n_{\mathrm{e}}·〈{\tilde{T}}_{\mathrm{e}}{\tilde{V}}_{\mathrm{r}}〉)$ [30]. The fluctuation data were sampled at 1MHz. The whole probe system was installed on a fast reciprocating manipulator with a scanning speed of 1.0 m s^-1 [31]. In this experiment, the deepest radial position plunged by the fast probe is about 3.8 cm inside the last closed flux surface (LCFS).

3.   Experimental results and discussion

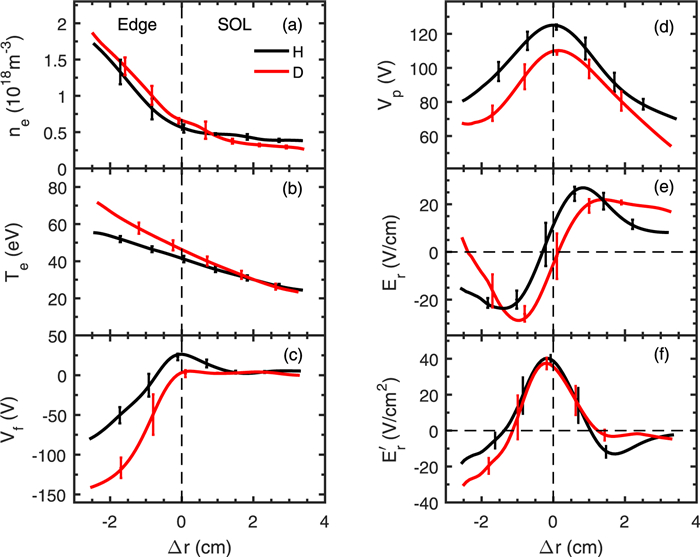
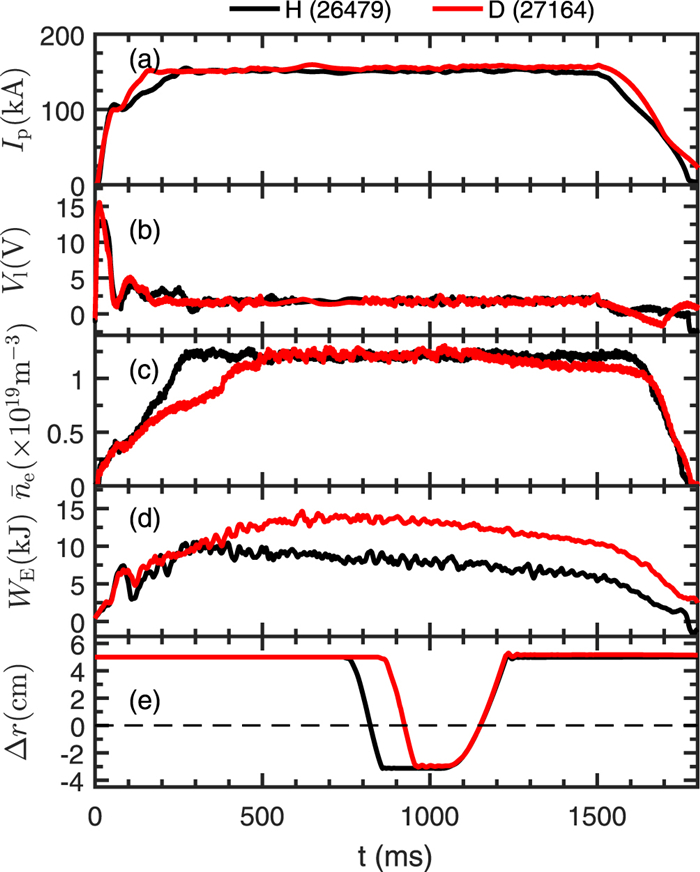
Typical discharge waveforms in H and D dominant plasmas are plotted in figure 1. It can be seen that with the same plasma current, loop voltage and line-averaged density, the plasma stored energy in D majority plasmas is higher than that in H ones, similar to those observed in other devices [4, 5, 7, 8, 10–12, 16]. Figure 1(e) shows time traces of the reciprocating Langmuir probes plunged in the stationary phase of the H and D discharges. The probe measurement in both discharges passed through approximately the same radial locations. It has been confirmed that the plasma horizontal position kept almost unchanged as the probes plunged into the plasma. Figure 2 depicts the edge equilibrium profiles averaged in several similar H (black) and D (red) majority discharges. Here, the ∆r = 0 denotes the LCFS location. As shown in figures 2(a) and (b), the local n_e and T_e in the edge region (inside the LCFS, ∆r < 0) are both enhanced in D plasmas, suggesting a higher edge pressure gradient, in agreement with higher stored energy achieved in the D plasma (see figure 1(d)). Inside the LCFS, both V_f and V_p are substantially lower in D plasmas than in H ones, leading to a slightly deeper E_r well and larger E_r shear ($E{\text{'}}_{\mathrm{r}}$) in the edge region of the D plasmas, as displayed in figures 2(e) and (f). To evaluate the role of the E_r shear in suppressing turbulence and turbulent transport, we have roughly estimated the mean E_r × B flow shear rates (${\omega }_{\mathrm{s}}\approx |E{\text{'}}_{\mathrm{r}}|/B_{\mathrm{T}}$) and compared them with local turbulence decorrelation rates ${\tau }_{\mathrm{c}}^{-1}$ (τ_c is the autocorrelation time of density fluctuations) in both H and D dominant plasmas. It is found that the ω_s increases from 2 × 10⁵ s^-1 in H plasmas to 3 × 10⁵ s^-1 in D plasmas in the plasma edge (∆r ≈ -2.5 cm). As both are comparable with the local turbulence decorrelation rate ${\tau }_{\mathrm{c}}^{-1}\approx (1-2)\times {10}^5{\mathrm{s}}^{-1}$, it is concluded that in the present experiment the mean E_r × B flow shear does not play a significant role in suppressing turbulent transport.

Figure  1.  Time traces of discharge waveforms in H (black curves) and D (red curves) majority plasmas. (a) Plasma current, (b) loop voltage, (c) central line-averaged density, (d) plasmas stored energy and (e) radial position of the reciprocating probes.

DownLoad: Full-Size Img PowerPoint

Figure  2.  Radial profiles of edge plasma parameters in H (black curves) and D (red curves) majority plasmas. (a) Plasma density, (b) electron temperature, (c) floating potential, (d) plasma potential, (e) radial electric field E_r and (f) E_r shear. The error bars indicate the standard deviation about the mean estimated in similar discharges.

DownLoad: Full-Size Img PowerPoint

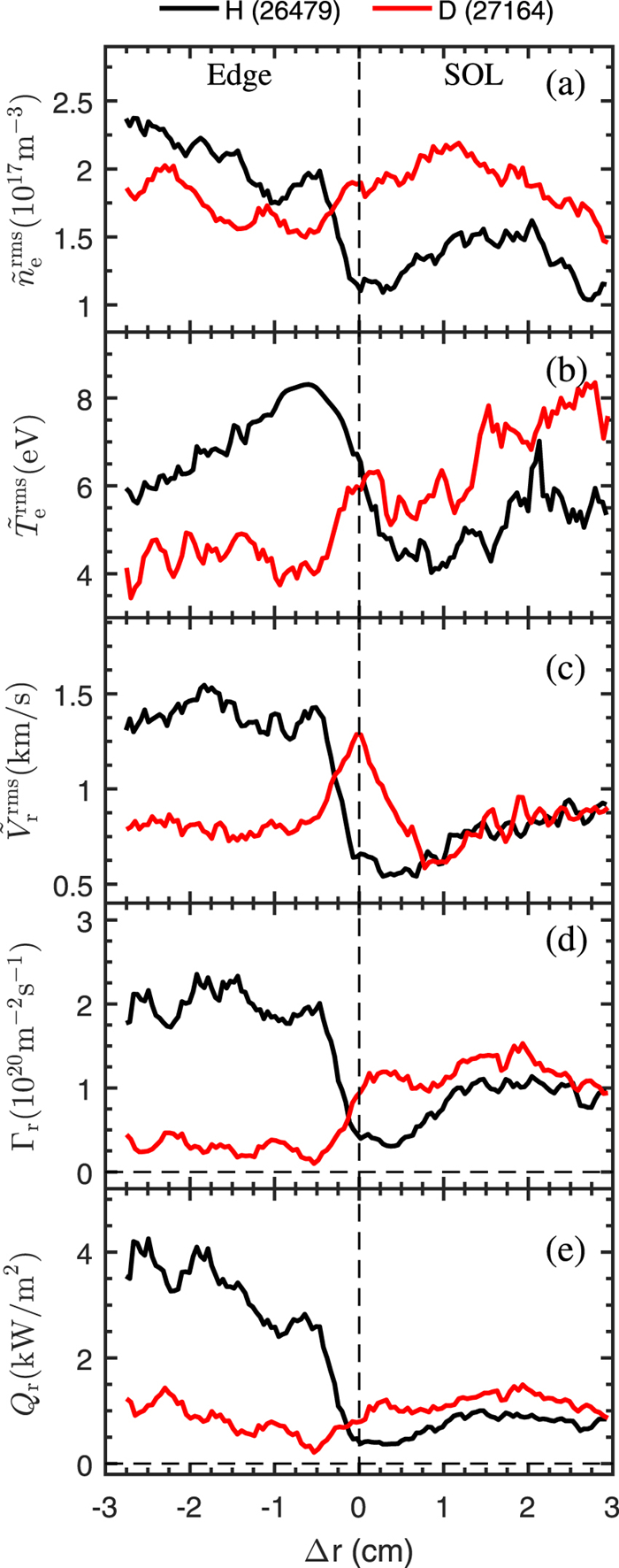
In order to gain an insight into the isotope effects on turbulence levels and associated transport, we compared the RMS values of density, electron temperature and radial velocity fluctuations, ${\tilde{n}}_{\mathrm{e}}^{\mathrm{rms}}$, ${\tilde{T}}_{\mathrm{e}}^{\mathrm{rms}}$ and ${\tilde{V}}_{\mathrm{r}}^{\mathrm{rms}}$, together with turbulence-induced particle flux Γ_r and Q_r measured in the same H and D discharges illustrated in figure 1. The results are shown in figure 3. It can be seen that in the edge region inside the LCFS the RMS values in density, electron temperature and radial velocity fluctuations are all lower in the D discharge (red curves). As a result, the turbulent particle and energy flux are also reduced in the edge of the D plasma. Thus, the lower thermal flux (Q_r) in the D plasma is consistent with the reduced plasma stored energy (W_E) observed in the D discharge (see figure 1(d)).

Figure  3.  Radial profiles of (a) rms level of density fluctuations, (b) rms level of electron temperature fluctuations, (c) rms level of radial velocity fluctuations, (d) fluctuation-driven particle flux and (e) fluctuation-driven energy flux measured by the fast reciprocating probe array in H (black curves) and D (red curves) majority plasmas.

DownLoad: Full-Size Img PowerPoint

To understand the mechanisms responsible for the reduction of turbulent transport in the isotope deuterium plasmas, we analyzed the spectrum characteristics of edge turbulence and zonal flows in H and D plasmas. In HL-2A, a low frequency coherent mode with long-range toroidal correlations, namely GAM zonal flows, has been routinely observed in floating potential signals [32, 33]. Theories predict that the GAM zonal flow has poloidally symmetric (m/n = 0/0) potential and asymmetric (m/n = 1/0) density perturbations [34, 35]. In the present experiments, it is found that the maximum GAM amplitude presents at ∆r ≈ -3 cm inside the LCFS [36]. Plotted in figure 4 are the frequency spectra of floating potential (${\tilde{V}}_{\mathrm{f}}$) and density (${\tilde{n}}_{\mathrm{e}}$) fluctuations detected at ∆r ≈ -3 cm in H and D majority plasmas averaged over several similar shots. As shown in figure 4(a), the ${\tilde{V}}_{\mathrm{f}}$ spectrum exhibits a sharp peak at f ≈ 8–10 kHz in both H and D plasmas, whereas the ${\tilde{n}}_{\mathrm{e}}$ spectrum displays quasi-coherent modes in higher frequency ranges.

Figure  4.  Frequency spectra of (a) floating potential fluctuations and (b) density fluctuations measured at ∆r ≈ -3 cm in H (black curves) and D (red curves) plasmas averaged over several similar shots.

DownLoad: Full-Size Img PowerPoint

According to theories [34, 35], the GAM frequency $f_{\mathrm{GAM}}^{\mathrm{th}}\approx C_{\mathrm{s}}\sqrt{2+1/q^2}/(2\pi R)$, where $C_{\mathrm{s}}=\sqrt{(T_{\mathrm{e}}+T_{\mathrm{i}})/m_{\mathrm{i}}}$ is the ion sound speed. The local safety factor at ∆r ≈ - 3 cm is q ≈ 3.8 for both H and D plasmas, as shown in figure 5, where the q profiles are computed from the two dimensional MHD equilibrium code EFIT [37], constrained by the external magnetic measurements and internal Faraday angle measurements. At ∆r ≈ - 3 cm, T_e ≈ 55 eV and 80 eV for H and D plasmas, respectively. Assuming that T_e ≈ T_i in both scenarios, we get $f_{\mathrm{GAM}}^{\mathrm{th}}\approx$ 10 kHz and 9 kHz for H and D plasmas, respectively. These results are close to the peaking frequencies in the ${\tilde{V}}_{\mathrm{f}}$ spectra of H and D plasmas. For GAM density fluctuations, it is predicted by theory [35] to have a $\sin \theta$ dependence, i. e., ${\tilde{n}}_{\mathrm{GAM}}\propto \sin \theta$, where θ is the poloidal angle. As the density fluctuations were measured near the midplane (θ ≈ 0), there should be no GAM activity appearing in ${\tilde{n}}_{\mathrm{e}}$ signals around f ≈ 8–10 kHz, just as we observed in figure 4(b). From figure 4, it is noted that (ⅰ) the GAM amplitude in H plasmas is much lower than that in D ones; (ⅱ) the density fluctuation power in the whole frequency range is substantially higher in H plasmas than that in D plasmas. In figure 5, it is shown that the local q values (at ∆r ≈ - 3 cm) in H and D plasmas are almost equal, suggesting that the Landau damping of GAM, described as exp(-q²), is nearly the same for the isotope plasmas in the present experiments. The obvious drop of the density fluctuation power in D plasmas appears to be related to stronger GAM zonal flows generated in the D plasmas. The results presented here imply a crucial role played by the isotope mass on the interaction between ambient turbulence and GAM zonal flows.

Figure  5.  Radial dependence of the safety factor calculated from the two dimensional MHD equilibrium code EFIT as a function of the radial position normalized by a.

DownLoad: Full-Size Img PowerPoint

To further compare the strength of the nonlinear coupling in turbulence between H and D plasmas, the squared auto-bicoherence [38], defined as b²(f₁, f₂) = |B(f₁, f₂)|²/(〈|X(f₁)X(f₂)|²〉〈|X(f₁ ± f₂)|²〉), where B(f₁, f₂) = 〈X(f₁)X(f₂)X^*(f₁ ± f₂)〉 and X(f) is the Fourier transform of the fluctuation signal x(t), has been computed. Figures 6(a) and (b) show contour-plots of the squared auto-bicoherence estimated by floating potential fluctuation signals measured at ∆r ≈ - 3 cm in D and H dominant plasmas. It is clear that the bicoherence along the f₂ = ±10 kHz and f₂ = - f₁ ± 10 kHz lines are much more prominent in D plasmas than that in H ones. This comparison illustrates stronger nonlinear coupling occurred between GAM zonal flows and turbulence in D plasmas. The summation of the squared bicoherence is calculated as $\sum b^2(f)=\sum b^2(f_1,f_2)/N(f){|}_{f=f_1\pm f_2}$, where N(f) is the number of Fourier components for each f in the summation. The result is depicted in figure 6(c). One can see a significant peak appeared at f ≈ 10 kHz in D plasmas, while in the H case the magnitude of ∑b²(f) is much weaker. The above results explicitly reveal that GAM zonal flows extract more energy via nonlinear interaction from ambient turbulence in D plasmas than in H plasmas. In figure 6(a), it is interesting to note that the nonlinear coupling between the GAM zonal flow and background turbulence takes place mainly in the high frequency range (f > 100 kHz). These results imply that the quasi-coherent mode turbulence displayed in figure 4(b) is driven linearly by plasma-free energy and does not interact with the GAM zonal flow. To further understand isotope effects on the driving mechanism of GAM zonal flows by the Reynolds stress dynamics, we have calculated the joint probability distribution function (joint-PDF) of the fluctuating poloidal (${\tilde{V}}_{\theta }$) and radial (${\tilde{V}}_{\mathrm{r}}$) velocities measured at ∆r ≈ -3 cm by the two step Langmuir probe arrays. Figure 7 shows the joint-PDF of ${\tilde{V}}_{\theta }$ and ${\tilde{V}}_{\mathrm{r}}$ computed by P = P(x, y) = N/N₀ (N is the number of events that occur in the time interval (x, x + ∆x) and (y, y + ∆y), where ∆x and ∆y are the bin dimensions of the x and y time series, and N₀ is the total number of events (data points)). It can be seen that the joint-PDF is not symmetrically distributed in the four quadrants. It has an elliptical shape across the first and the third quadrants in both H and D plasmas. It is due to the asymmetric distribution that results in a non-zero Reynolds stress. Apparently, in D plasmas the Reynolds stress tensor $〈{\tilde{V}}_{\mathrm{r}}{\tilde{V}}_{\theta }〉$ is much more asymmetric than that in H ones, suggesting a stronger Reynolds stress drive for the generation of GAM zonal flows in D plasmas. Moreover, it is found that the tilting angle of the Reynolds stress tensor, ${\tilde{V}}_{\theta }/{\tilde{V}}_{\mathrm{r}}$, is also larger in D plasmas, implying a larger tilting angle of the turbulence eddy structure as ${\tilde{V}}_{\theta }/{\tilde{V}}_{\mathrm{r}}\propto {\tilde{E}}_{\mathrm{r}}/{\tilde{E}}_{\theta }\propto k_{\mathrm{r}}/k_{\theta }$. These results are consistent with stronger E_r × B shear flows detected in D plasmas (see figure 2(f)) for effectively tilting the eddy structure and hence symmetry-breaking of the Reynolds stress, as pointed out earlier in references [39, 40]. The experimental measurements also show that in the plasma edge region the poloidal and radial correlation lengths (l_θ and l_r) of turbulence are substantially larger in D plasmas than those in H ones [36], in accordance with previous observations [14, 41, 42] and theoretical calculations [43].

Figure  6.  Contour-plot of the squared auto-bicoherence of V_f fluctuations (a) in H plasmas and (b) in D plasmas. Shown in (c) is the summed squared auto-bicoherence in H (black curves) and D (red curves) plasmas. The horizontal dotted line indicates the statistical noise level.

DownLoad: Full-Size Img PowerPoint

Figure  7.  Contour-plot of the joint-PDF of the Reynolds stress tensor between poloidal velocity fluctuations (${\tilde{V}}_{\theta }$) and radial velocity fluctuations (${\tilde{V}}_{\mathrm{r}}$) in H (left side) and D (right side) dominant plasmas. The PDF values are normalized by the maximum one.

DownLoad: Full-Size Img PowerPoint

4.   Summary

In summary, the isotope effects on plasma confinement, edge turbulence and turbulent transport as well as GAM zonal flows have been studied using a two-step Langmuir probe array in H and D majority plasmas in the HL-2A tokamak. Evidence shows that under similar discharge parameters the D plasma has better confinement and lower turbulent transport than the H plasma. Meanwhile, it is observed that the magnitude of GAM zonal flows, the tilting angle of the Reynolds stress tensor, and the turbulence correlation lengths are all larger in the edge region of the D plasma. The results provide direct experimental proof on the importance of the nonlinear energy transfer between turbulence and zonal flows for governing the isotope effects in fusion plasmas.