On the evolution and formation of discharge morphology in pulsed dielectric barrier discharge

1.   Introduction

Electron cyclotron resonance heating (ECRH) is a well-known and widely used technique for heating electrons in fusion devices. Regimes with pure ECRH are suggested to be a simulator for burning plasma [1, 2]. Ions in such regimes are heated only by Coulomb collisions with electrons that provide a broad ion heat source.

Unfortunately, the central ion temperature in ECRH regimes does not tend to be high, even in high-ECRH power experiments (see for example the most recent results from W7-X [3]). The injection of ECRH leads to an increase in turbulent transport that compensates the possible increase of the ion heat source $P_{\rm {ei}}\propto \dfrac{T_{\rm e} - T_{\rm{i}}}{T_{\rm e}^{1.5}}n_{\rm e}^2$ due to the rise of $(T_{\rm e}-T_{\rm{i}})$.

It is shown on LHD that neutral beam heating injection may help to achieve a simultaneously high $T_{\rm e}$ and high $T_{\rm{i}}$ regime [4]. However, the ion temperature profile flattens in the central region $\rho < 0.3$ due to the on-axis ECRH. The increase in ion heat transport in regimes with ECRH is also observed in DIII-D: by a factor of $\sim 6$ in L-mode [5] and by a factor of $\sim 1.5$−3 in H-mode [6]. The most comprehensive analysis of electron and ion heat transport in L-mode regimes on ASDEX Upgrade using the quasilinear gyrokinetic transport model TGLF [7] can be found in reference [8]. The authors managed not only to reproduce electron and ion temperatures, but also to model their dependencies on general engineering plasma parameters. However, TGLF-SAT2 predictions overestimate ion heat transport in high-ECRH power regimes, which results in the underestimation of the central ion temperature.

The vast majority of published studies of ion heat transport in ECRH regimes are limited to on-axis ECRH, while off-axis heating has not been considered in detail. In this study, we aimed to investigate in which regimes high anomalous ion heat transport can be obtained, and how it is related to the different ECRH regimes.

2.   Experimental setup

The description of the T-10 tokamak and its diagnostic complex used for power balance analysis is given in reference [9]. For the purposes of this work, we use the following diagnostics:

• CXRS diagnostics for ion temperature, $T_{\rm{i}}$, and light impurity density measurements, $n_Z$;

• 16-channel interferometry for electron density measurements, $n_{\rm e}$;

• ECE diagnostics and soft X-ray spectroscopy for measurements of electron temperature, $T_{\rm e}$;

• bremsstrahlung diagnostics in visible region for effective ionic charge measurements, $Z_{\rm {eff}}$;

• passive spectroscopy in visible range for control of impurities and working gas atom influx.

We consider regimes with ECR heating with second-harmonic extra-ordinary mode. There are three available gyrotrons on T-10:

(1) “A”: $P_{\rm {EC}}\leqslant1$ MW, $f =140$ GHz, 200 ms length, can be rotated in poloidal rotation, co-electron cyclotron current drive (ECCD).

(2) “B”: $P_{\rm {EC}} \leqslant0.5$ MW, $f =129$ GHz, 400 ms length, injection perpendicular to current direction.

(3) “C”: $P_{\rm {EC}}\leqslant1$ MW, frequency $f =140$ GHz, 200 ms length, can be rotated in toroidal rotation, co-/counter-ECCD.

We distinguish the three regimes of ECRH with regard to the sawtooth inversion radius, which varies within the range $\rho_{\rm S}=0.17$–0.33 in the Ohmic heating stage:

(1) Off-axis, if resonance zone is outside $\rho_{\rm S}$.

(2) On-axis, if resonance zone is inside $\rho_{\rm S}$.

(3) Mixed, if off-axis and on-axis heating are presented simultaneously.

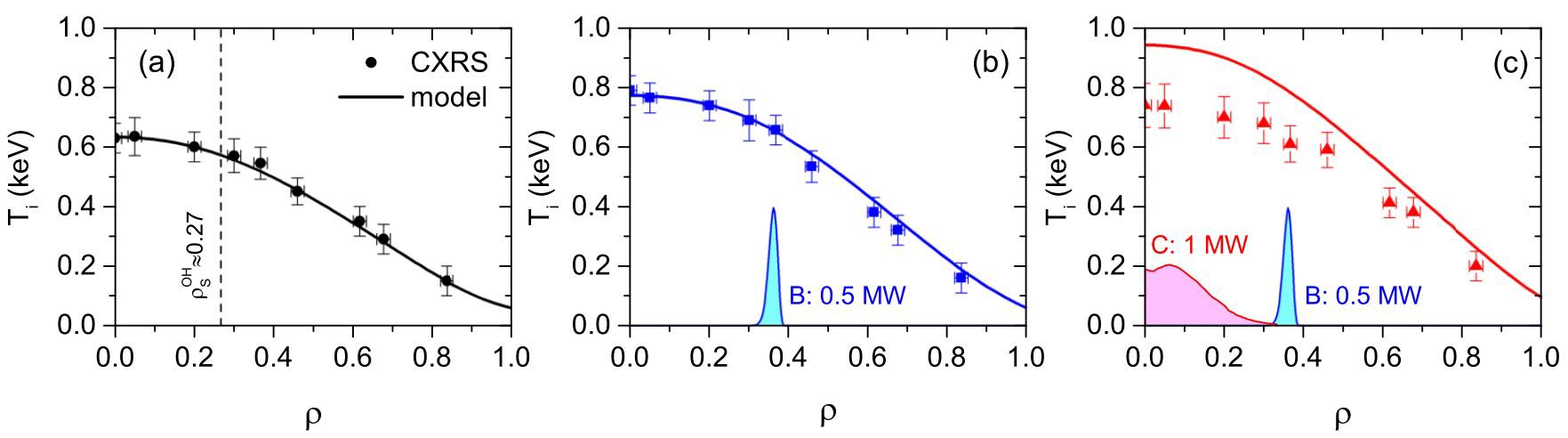
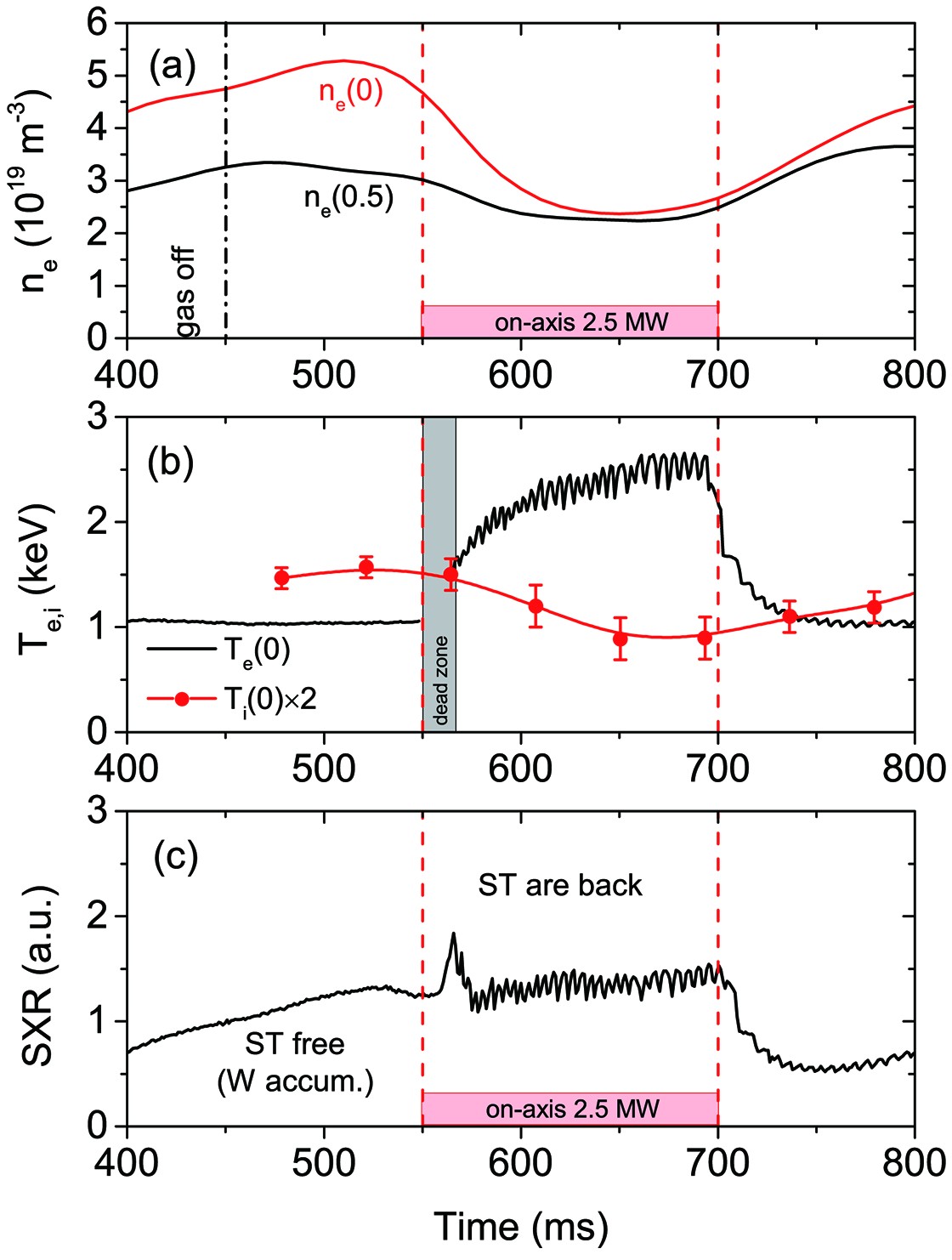
An example of a shot with on-axis heating is presented in figure 1. In shot 72052, ECRH started at 550 ms with all three gyrotrons (injected power $P_{\rm {EC}} = 2.5$ MW). Due to the pump-out effect [10], the electron density profile, $n_{\rm e}(\rho)$, becomes flatter. The central electron temperature, $T_{\rm e}(0)$, rises up to 2.5 keV while the ion temperature, $T_{\rm{i}}(0)$, decreases from 0.7 keV to 0.45 keV. The sawtooth activity that was suppressed by impurity accumulation during the Ohmic stage is restored as a result of impurity removal [11]. The possible change of toroidal rotation [12] with ECRH is not observed in T-10. The reason is the very low values of toroidal rotation velocities ($\sim10-15$ km/s), which is the diagnostic sensitivity limit. After switching the ECRH off, the density and temperatures return to their Ohmic values.

Figure  1.  Time evolution of plasma parameters in shot 72052 ($\bar{n}_{\rm e}=3\times10^{19}\;$m$^{-3}$, $I_{\rm {pl}} = 220$ kA, $B_{\rm {t0}} = 2.4$ T, $q_a = 3.3$) with on-axis ECRH: (a) electron density, (b) electron and ion temperatures, and (c) SXR signal.

DownLoad: Full-Size Img PowerPoint

The off-axis and mixed ECRH are shown in figure 2. The off-axis gyrotron B starts at 570 ms with $P_{\rm {EC}} = 0.5$ MW, and results in density peaking and a slight electron $T_{\rm e}(0)$ (from 0.95 to 1.2 keV) and ion $T_{\rm{i}}(0)$ (from 0.6 to 0.8 keV) increase. The sawteeth at the off-axis stage are suppressed due to the electron temperature broadening. It is necessary to note that off-axis ECRH leads to impurity density peaking due to the formation of positive convective velocities [13, 14]. Such effects are also observed in the considered discharges but they go beyond the scope of the present work. At 775 ms, on-axis gyrotron C with $P_{\rm {EC}}=1$ MW and $18{\text{°}}$ counter-ECCD starts. While $n_{\rm e}(\rho)$ flattening does not appear, gyrotron C gives rise to the effects of the on-axis heating: $T_{\rm e}(0)$ increases and $T_{\rm{i}}(0)$ decreases. Due to the counter-ECCD injection, the sawteeth remain suppressed and MHD activity is not observed.

Figure  2.  Time evolution of plasma parameters in shot 71869 ($\bar{n}_{\rm e}=4\times10^{19}\;$m$^{-3}$, $I_{\rm {pl}} = 200$ kA, $B_{\rm {t0}} = 2.48$ T, $q_a = 3.7$) with off-axis and mixed ECRH: (a) electron density, (b) electron and ion temperatures, and (c) SXR signal.

DownLoad: Full-Size Img PowerPoint

3.   Ion temperature predictive modeling

In this section we examine if the change of plasma parameters is enough to describe the reduction of ion temperature in ECRH regimes. To do so we use an empirical scaling of anomalous ion heat conductivity [9] obtained for Ohmic regimes to calculate ion temperature profiles. The ion heat conductivity is taken as follows:

where $\chi_{\rm{i}}^{\rm {neo}}$ is the neoclassical heat conductivity calculated using the NCLASS code [15], $\chi_{\rm {i-scaling}}^{\rm {an}}$ is the scaling for the Ohmic regimes on T-10 [9], $\chi_{\rm {ST}}=r_{\rm {ST}}^2/\tau_{\rm {ST}}$ is the ion heat conductivity inside the sawtooth inversion radius, and $\tau_{\rm {ST}}$ is the sawtooth oscillation period. In sawtooth-free regimes, $\chi_{\rm {ST}}=0$. The electron temperature and density profiles are prescribed and taken from measurements.

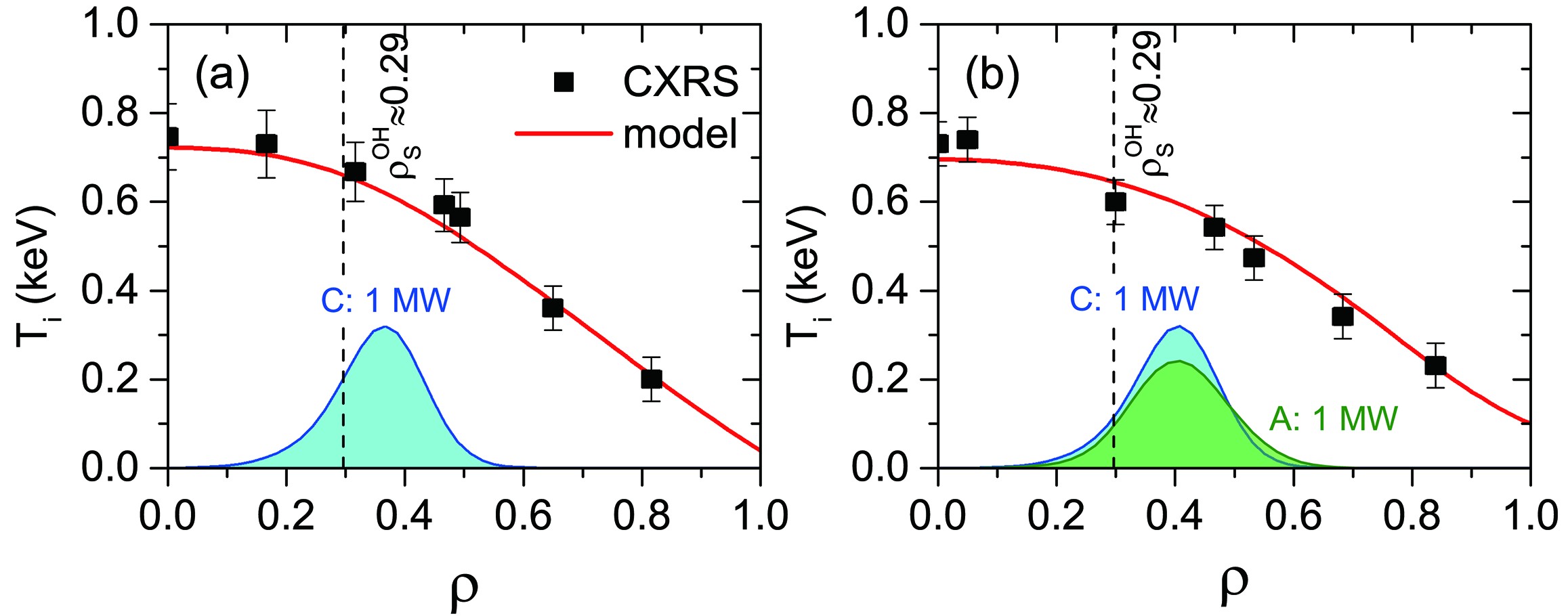
Figure 3 shows the modeling results for shot 71864. This shot is sawtooth-free at the ECRH stages. Both the Ohmic and the off-axis ECRH stages with 0.5 MW are well described by the model (1) (see figures 3(a) and (b)). At the stage with mixed heating, the calculated $T_{\rm{i}}$ exceeds the experimental points by $\sim100$ eV in the center.

Figure  3.  Simulation of ion temperature profile in shot 71864 ($\bar{n}_{\rm e}=4\times10^{19}$ m$^{-3}$, $I_{\rm {pl}} = 220$ kA, $B_{\rm {t0}} = 2.48$ T, $q_a = 3.4$): (a) Ohmic stage; (b) off-axis stage with gyrotron B ($P_{\rm {EC}}=0.5$ MW); (c) mixed stage with off-axis gyrotron B ($P_{\rm {EC}}=0.5$ MW) and on-axis C ($P_{\rm {EC}}=1.0$ MW, $18{\text{°}}$ counter-ECCD). The power deposition profiles are given by the curves with the filled area.

DownLoad: Full-Size Img PowerPoint

In shots 72769 and 72983 the off-axis ECRH is applied with higher power. As shown in figure 4, the calculated ion temperature is matched well within the measurements even with 2 MW heating and suppressed sawtooth oscillation.

Figure  4.  Simulation of ion temperature profile in shots with off-axis ECRH: (a) 72769 ($\bar{n}_{\rm e}=3.7\times10^{19}\;$m$^{-3}$, $I_{\rm {pl}} = 220$ kA, $B_{\rm {t0}} = 2.25$ T, $q_a = 3.1$) with gyrotron C ($P_{\rm {EC}}=1.0$ MW, $18{\text{°}}$ co-ECCD); (b) 72983 ($\bar{n}_{\rm e}=3.5\times10^{19}\;$m$^{-3}$, $I_{\rm {pl}} = 220$ kA, $B_{\rm {t0}} = 2.24$ T, $q_a = 3.1$) with gyrotrons A ($P_{\rm {EC}}=1.0$ MW, $8{\text{°}}$ co-ECCD) and C ($P_{\rm {EC}}=1.0$ MW, $18{\text{°}}$ co-ECCD). The power deposition profiles are given by the curves with the filled area.

DownLoad: Full-Size Img PowerPoint

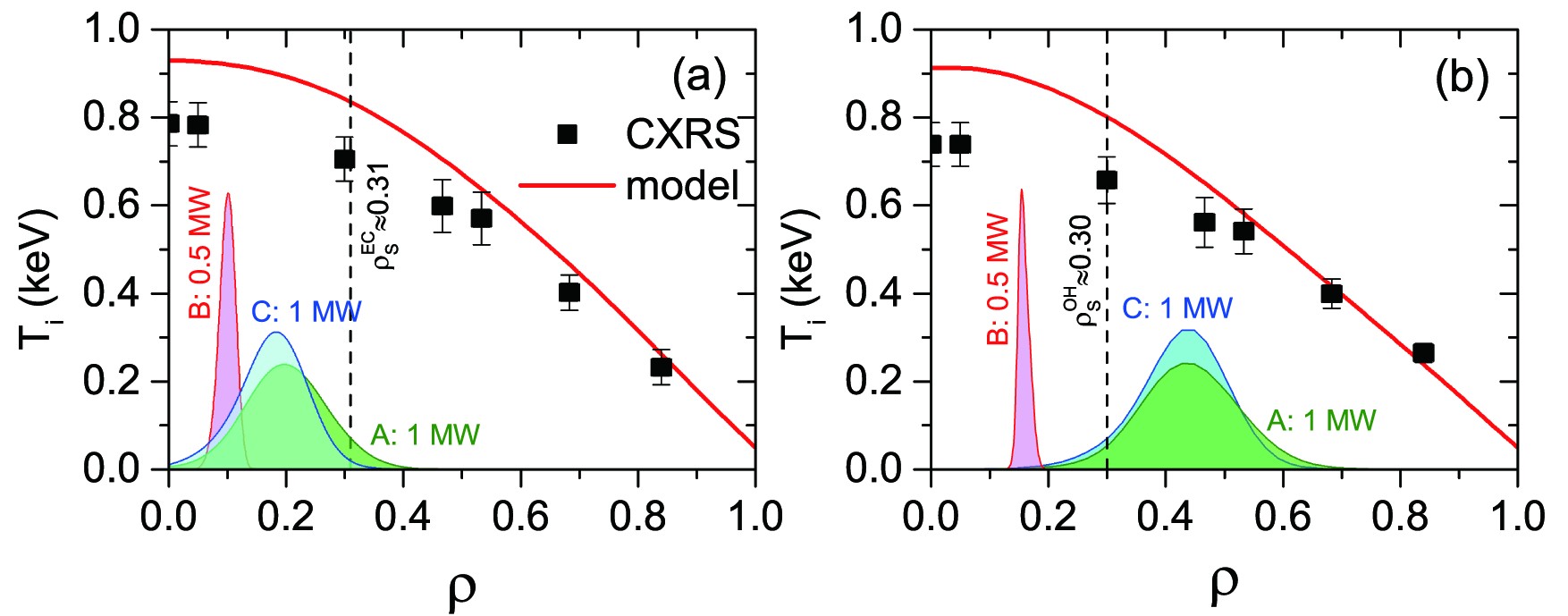
On-axis heating with 2.5 MW does not exhibit a significant change in the values of $T_{\rm{i}}$ modeled by (1). One can see in figures 5(a) and (b) that the excess by $\sim100$ eV at the center persists regardless of the on-axis ECRH power. It also seems to be irrelevant whether the EC injection is co-ECCD or counter-ECCD, and whether the discharge has sawtooth oscillations or not.

Figure  5.  Simulation of ion temperature profile in shots with high-power ECRH: (a) 72889 ($\bar{n}_{\rm e}=3.6\times10^{19}\;$m$^{-3}$, $I_{\rm {pl}} = 220$ kA, $B_{\rm {t0}} = 2.35$ T, $q_a = 3.2$) with gyrotrons A ($P_{\rm {EC}}=1.0$ MW, $8{\text{°}}$ co-ECCD), C ($P_{\rm {EC}}=1.0$ MW, $18{\text{°}}$ co-ECCD), and B ($P_{\rm {EC}}=0.5$ MW); (b) 72888 ($\bar{n}_{\rm e}=3.6\times10^{19}\;$m$^{-3}$, $I_{\rm {pl}} = 220$ kA, $B_{\rm {t0}} = 2.22$ T, $q_a = 3$) with off-axis gyrotrons A ($P_{\rm {EC}}=1.0$ MW, $8{\text{°}}$ co-ECCD), C ($P_{\rm {EC}}=1.0$ MW, $18{\text{°}}$ co-ECCD), and on-axis B ($P_{\rm {EC}}=0.5$ MW). The power deposition profiles are given by the curves with the filled area.

DownLoad: Full-Size Img PowerPoint

Therefore, for some shots, model (1) (and even more so neoclassical heat conductivity) overestimates the experimental data and the increase of transport coefficients is required.

4.   Influence of ECRH localization

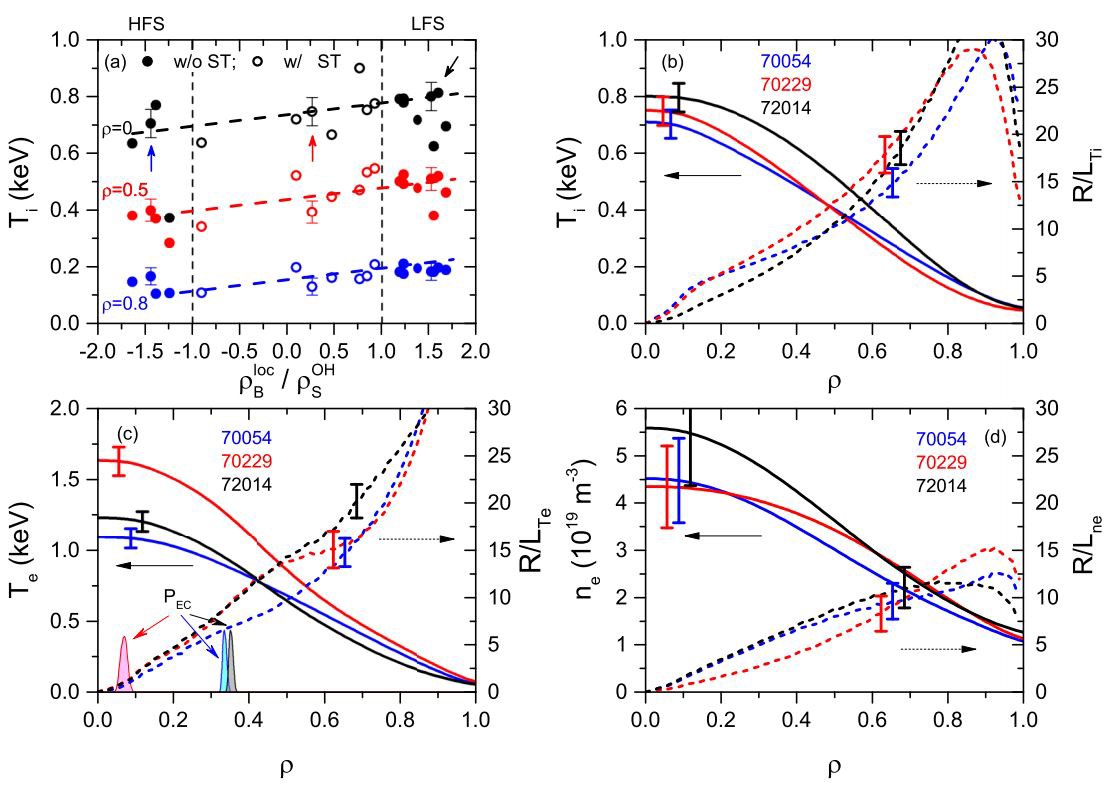
In order to analyze how the position of ECR heating affects the ion heat conductivity, we change the toroidal magnetic field, $B_{\rm {t0}}$, to shift the EC resonance zone of the gyrotron B – $\rho_{\rm B}^{\rm {loc}}$. The variance of $B_{\rm {t0}} = 2.15$–2.53 T corresponds to the change of $\rho_{\rm B}^{\rm {loc}}$ from $-0.41$ (high-field side, HFS) to 0.45 (low-field side, LFS). The resonance zone position is calculated using OGRAY code [16]. Being directed perpendicular to the magnetic field gyrotron B provides a narrow power deposition profile and zero current drive. It allows us to use the loop voltage and sawtooth inversion radius as indicators for gross errors of $T_{\rm e}(r)$ by modeling the current density profile. Selected for analysis discharges are done with $I_{\rm {pl}}=180$–250 kA, which corresponds to $q_a=2.9$–3.72. While the majority of experiments have been performed with $I_{\rm {pl}}=220$ kA, we have to consider the different plasma currents to cover the maximal possible range of EC resonance positions.

In ECR-heated plasma with the gyrotron B ion temperature is higher in shots with higher $B_{\rm {t0}}$. As shown in figure 6(a), off-axis heating on the LFS (points with $\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}>1.0$) provides higher $T_{\rm{i}}$ by $20\%$–$30\%$. On-axis heating (points $-1.0<\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}<1.0$) is obtained in the presence of sawteeth. The three arrows indicate three shots that are used for profile analysis. The selection criterion is the smallest deviation from the $T_{\rm{i}}(0)$ trend.

Figure  6.  Change of plasma parameter in scan over resonance position of gyrotron B. (a) Ion temperatures for three radial points. Arrows indicate shots 70054 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=-1.44$, $I_{\rm {pl}}=190$ kA, $B_{\rm {t0}}=2.19$ T, $q_a=3.5$), 70229 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=0.27$, $I_{\rm {pl}}=220$ kA, $B_{\rm {t0}}=2.3$ T, $q_a=3.1$), and 72014 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=1.54$, $I_{\rm {pl}}=218$ kA, $B_{\rm {t0}}=2.48$ T, $q_a=3.4$) that used for profile analysis. (b) Ion temperature profiles. (c) Electron temperature profiles (power deposition profiles are given by curves with filled area). (d) Electron density profiles.

DownLoad: Full-Size Img PowerPoint

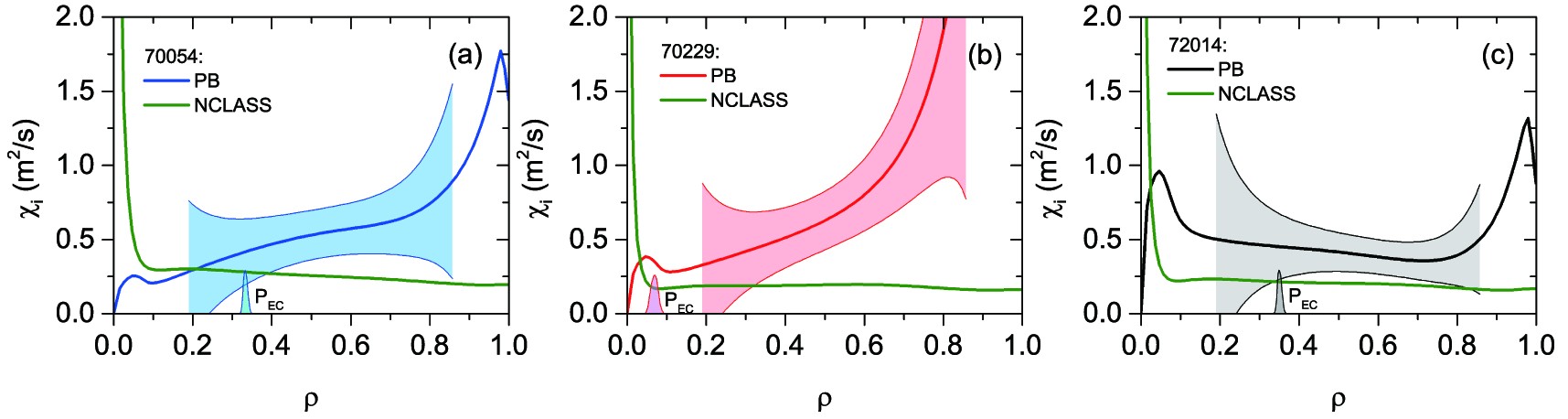
Kinetic profiles for shots 70054 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=-1.44$), 70229 ($\rho_{\rm {B}}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=0.27$), and 72014 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=1.54$) are given in figures 6(b)–(d). The ion temperature is more peaked in the case of on-axis heating. In zone $\rho>0.5$, the normalized gradient length, $R/L_{T_{\rm{i}}}$, is higher in the case of on-axis and LFS off-axis ECRH. Clearly, the electron temperature is higher with on-axis ECRH, but the normalized gradient length, $R/L_{T_{\rm e}}$, is almost the same in comparison with the LFS off-axis ECRH. The electron density is flattening with the on-axis heating due to the density pump-out effect. The LFS and HFS off-axis ECRH provides similarly peaked density profiles.

HFS off-axis ECRH results in lower electron temperature gradients than LFS off-axis ECRH. Herewith the density stays narrow, and its normalized gradient length, $R/L_{n_{\rm e}}$, is comparable to $R/L_{T_{\rm{i}}}$ in $\rho=0.4$–0.7.

To obtain the ion heat conductivity we use the power balance technique:

where $Q_{\rm{i}}$ is the ion heat flux, $n_{\rm{i}}$ is the ion density, $P_{\rm {ei}}$ is the electron to ion heat transfer due to Coulomb collisions [17], $P_{\rm {CX}}$ is the loss due to the charge exchange of deuterons with deuterium atoms, $\Gamma_{\rm{i}}$ is the ion particle flux, $S_\rho$ is the magnetic surface area, and $V^{\prime}$ is the volume derivative. More details on the ion power balance methodology and its sensitivity analysis on T-10 can be found in reference [9].

The ion heat conductivity profiles obtained by equation (2) are presented in figures 7(a)–(c) in comparison with neoclassical heat conductivity, $\chi_{\rm{i}}^{\rm {neo}}$, calculated using NCLASS code [15]. Whereas the highest excess over neoclassical theory is observed with on-axis ECRH, HFS off-axis ECRH gives $\chi_{\rm{i}}^{\rm {PB}}$ very close to $\chi_{\rm{i}}^{\rm {neo}}$. Let us distinguish the anomalous heat flux, $Q_{\rm{i}}^{\rm {an}}$, by subtracting the neoclassical flux, $Q_{\rm{i}}^{\rm {neo}}=-\chi_{\rm{i}}^{\rm {neo}}n_{\rm{i}}\dfrac{\partial T_{\rm{i}}}{\partial \rho}$, from the numerator in equation (2):

Figure  7.  Ion heat conductivity profiles for shots: (a) 70054 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=-1.44$, $I_{\rm {pl}}=190$ kA, $B_{\rm {t0}}=2.19$ T, $q_a=3.5$), (b) 70229 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=0.27$, $I_{\rm {pl}}=220$ kA, $B_{\rm {t0}}=2.3$ T, $q_a=3.1$), (c) 72014 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=1.54$, $I_{\rm {pl}}=218$ kA, $B_{\rm {t0}}=2.48$ T, $q_a=3.4$). Shaded areas are errors in trusted region. Power deposition profiles are given by curves with filled area.

DownLoad: Full-Size Img PowerPoint

In order to make heat flux a transport characteristic it is possible to divide it by $n_{\rm{i}}\dfrac{\partial T_{\rm{i}}}{\partial \rho}$ and obtain the quasilinear heat conductivity coefficient as in equation (2). Another opportunity is to divide it by the ion pressure $n_{\rm{i}} T_{\rm{i}}$ to obtain the quantity with the dimension of (m/s). The relation of these two approaches is obvious:

Since we consider regimes without auxiliary ion heating, the ion temperature gradients do not change significantly ($R/L_{T_{\rm{i}}}=15\pm5$). Therefore, the change in normalized heat flux directly reflects the change in the transport coefficient.

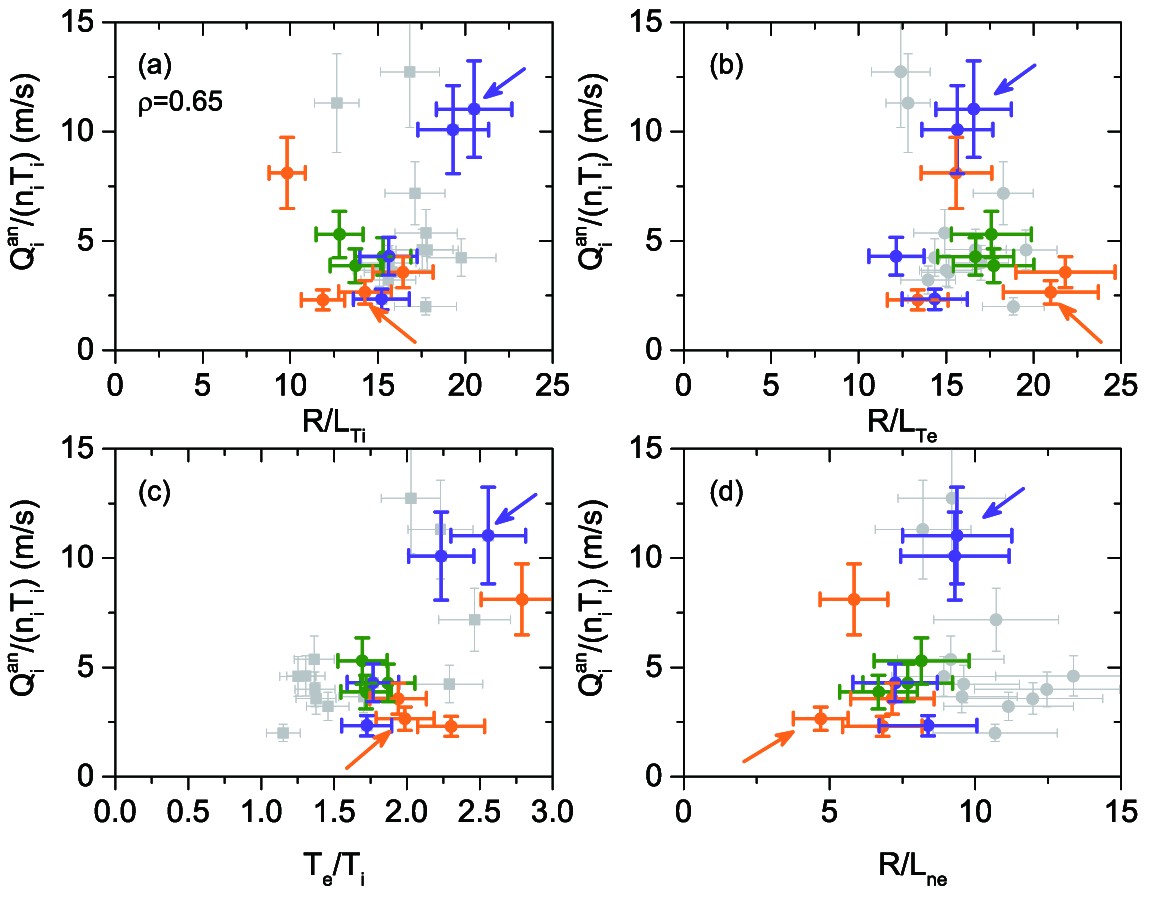
One can see in figure 8 that the normalized anomalous ion heat flux would be higher in shot 70229. The dependence of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ on $R/L_{T_{\rm{i}}}$ is given in figure 9(a). While we can obtain high and low values of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ in all three heating regimes, the trend is different. On-axis ECRH provides a positive slope. LFS off-axis ECRH provides a negative slope that could be considered as a “negative stiffness” effect [1, 18]. It is possible to see in figure 9(b) that similar dependencies are observed on $R/L_{T_{\rm e}}$. It is shown in figure 9(c) that a high $T_{\rm e}/T_{\rm{i}}$ ratio correlates with high $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ values.

Figure  8.  Radial profiles of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ parameter for shots: 70054 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=-1.44$, $I_{\rm {pl}}=190$ kA, $B_{\rm {t0}}=2.19$ T, $q_a=3.5$), 70229 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=0.27$, $I_{\rm {pl}}=220$ kA, $B_{\rm {t0}}=2.3$ T, $q_a=3.1$), and 72014 ($\rho_{\rm B}^{\rm {loc}}/\rho_{\rm S}^{\rm {OH}}=1.54$, $I_{\rm {pl}}=218$ kA, $B_{\rm {t0}}=2.48$ T, $q_a=3.4$).

DownLoad: Full-Size Img PowerPoint

Figure  9.  Dependence of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ at $\rho=0.65$ on: (a) ion temperature gradient, (b) electron temperature gradient, (c) ratio $T_{\rm e}/T_{\rm{i}}$ at $\rho=0.65$, (d) density gradient. Arrows indicate shots 70054 (blue), 70229 (red), and 72014 (black).

DownLoad: Full-Size Img PowerPoint

An interesting result can be seen in figure 9(d). Higher density gradients correlate with a lower $T_{\rm e}/T_{\rm{i}}$ ratio and lower anomalous ion heat flux. It seems that in the T-10 plasma electron and ion turbulent modes exist simultaneously and their interaction could determine the ion heat transport. It would also explain the strictly opposite dependencies on the plasma parameters of the ion heat conductivity compared to the electron heat conductivity [19] and impurity diffusion [20].

Together with plasma parameters and their gradients, the ion–ion $\nu_{\rm {ii}}^{\ast}$ and electron–ion $\nu_{\rm {ei}}^{\ast}$ collisionalities are also changed. Figure 10 shows the dependence on collisionalities calculated for the middle radius $\rho = 0.5$ as follows [21]:

Figure  10.  Dependence of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ at $\rho=0.65$ on ion–ion (a) and electron–ion (b) collisionalities. Arrows indicate shots 70054 (blue), 70229 (red), and 72014 (black).

DownLoad: Full-Size Img PowerPoint

where $\nu_{\rm {ii}}$ and $\nu_{\rm {ei}}$ are ion–ion and electron–ion Coulomb collisions frequencies, respectively, $m_{\rm d}$ and $m_{\rm e}$ are the deuteron and electron masses, $R_0$ is the major radius, $r$ is the local minor radius, and $q$ is the safety factor.

High values of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ correspond to high ion–ion collisionality, as shown in figure 10(a). Moreover, the change of $\nu_{\rm {ii}}^{\ast}$ is responsible for the negative slope observed for LFS off-axis ECRH points in figure 9(a). The dependence on the electron–ion collisionality is rather flat (see figure 10(b) for both high and low $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ regimes.

5.   Influence of ECRH power

In this section we consider on-axis and mixed ECRH with different power. In order to perform the scan over EC power we choose shots with one (B), two (B and C), or three (A, B, and C) gyrotrons. The absorbed power, $P_{\rm {EC}}^{\rm {abs}}$, is calculated using the OGRAY code. With higher $P_{\rm {EC}}^{\rm {abs}}$, the central electron temperature is higher while the central ion temperature does not change significantly. This result is shown in figure 11.

Figure  11.  Dependence of electron and ion central temperatures on absorbed ECRH power. Colour distinguishes power group for further figures: purple – gyrotron B, green – gyrotrons B and C, orange – gyrotrons A, B, and C.

DownLoad: Full-Size Img PowerPoint

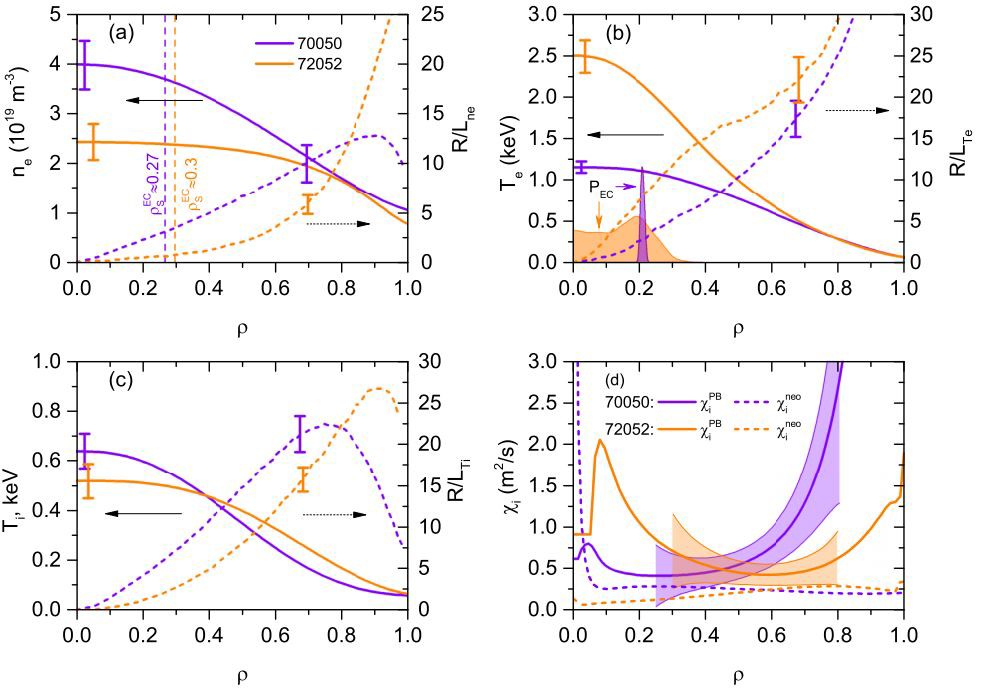
The parameter profiles are given in figures 12(a)–(c) for two shots with low ($P_{\rm {EC}}^{\rm {abs}} = 0.4$ MW) and high ($P_{\rm {EC}}^{\rm {abs}} =$ 1.88 MW) ECRH power. The density profile is significantly flatter in shot 72052 ($P_{\rm {EC}}^{\rm {abs}} = 1.88$ MW). Its normalized gradient lengths approximately lower by a factor of 2 compared with shot 70050 ($P_{\rm {EC}}^{\rm {abs}} = 0.4$ MW). Higher on-axis power heating results in a higher $T_{\rm e}$ in the central region and higher electron temperature gradients. While $T_{\rm{i}}(0)$ remains almost unchanged, the ion temperature profile flattens with the $P_{\rm {EC}}$ increase. Figure 12(d) shows the resulting ion heat conductivity. In plasma with high ion heat transport power balance conductivity exceeds neoclassical one up to 10 times.

Figure  12.  Change of plasma parameters in discharges with different ECRH power: 70050 ($P_{\rm {EC}}^{\rm {abs}} = 0.4$ MW, $I_{\rm {pl}}=190$ kA, $B_{\rm {t0}}=2.24$ T, $q_a=3.53$) and 72052 ($P_{\rm {EC}}^{\rm {abs}} = 1.88$ MW, $I_{\rm {pl}}=220$ kA, $B_{\rm {t0}}=2.4$ T, $q_a=3.27$). (a) Electron density and its normalized gradient lengths, (b) electron temperature and its normalized gradient lengths (power deposition profiles are given by curves with filled area), (c) ion temperature and its normalized gradient lengths, (d) ion heat conductivity from power balance and NCLASS code.

DownLoad: Full-Size Img PowerPoint

Let us consider again the dependencies of the normalized anomalous heat flux $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ at $\rho=0.65$ on the different plasma parameters. Plots are given in figures 13(a)–(c). The colour of the dots indicates the power group from figure 11. The gray dots are reproduced from figure 9. A higher EC power results in a lower $R/L_{T_{\rm{i}}}$ and higher $R/L_{T_{\rm e}}$, which corresponds to a lower anomalous ion heat flux (see figures 13(a) and (b)). In comparison with the scan over resonance zone, the power scan does not provide us with a greater $T_{\rm e}/T_{\rm{i}}$ range at $\rho=0.65$ (see figure 13(c)), and the tendency is the same: a higher $T_{\rm e}/T_{\rm{i}}$ corresponds to a higher $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$. The dependence on $R/L_{n_{\rm e}}$ looks different to figure 9(d). One can see in figure 13(d) that a higher EC power leads to lower density gradient lengths. Points with lower $R/L_{n_{\rm e}}$ allow us to see that a high $T_{\rm e}/T_{\rm{i}}$ ratio can be obtained only with a certain $R/L_{n_{\rm e}} =6-10$.

Figure  13.  Dependence of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ at $\rho=0.65$ on: (a) ion temperature gradient, (b) electron temperature gradient, (c) ratio $T_{\rm e}/T_{\rm{i}}$ at $\rho=0.65$, (d) density gradient. colour indicates power group from figure 11. Gray points are taken from resonance zone shift variation presented in figure 9.

DownLoad: Full-Size Img PowerPoint

In contrast to figure 10(a), the $P_{\rm {EC}}$ scan does not show such a clear dependence on $\nu_{\rm {ii}}^{\ast}$ (see figure 14(a)). Points with low $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ that are obtained with low $R/L_{n_{\rm e}}$ are independent or have an inverse dependence on $\nu_{\rm {ii}}^{\ast}$. Flat dependence of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ on $\nu_{\rm {ei}}^{\ast}$ is also obtained in shots with various ECRH power, as shown in figure 14(b).

Figure  14.  Dependence of $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ at $\rho=0.65$ on ion–ion (a) and electron–ion (b) collisionalities. Colour indicates power group from figure 11. Gray points are taken from resonance zone shift variation presented in figure 9.

DownLoad: Full-Size Img PowerPoint

6.   Conclusion and discussion

Ion heat transport is investigated in ECR-heated L-mode plasma on the T-10 tokamak by means of the power balance technique. The high and low ion heat transport regimes are observed in both off-axis and on-axis ECRH plasmas. Quasi-linear heat conductivity $\chi_{\rm{i}}^{\rm {PB}}$ in high transport discharges can exceed the neoclassical level up to 10 times. The predictive modeling using Ohmical scaling of anomalous and neoclassical ion heat conductivities overestimates the ion temperature in high transport regimes by $\sim100$ eV, and describes it well in the low transport discharges.

The analysis of two scans, ECRH resonance position and ECRH power, is performed. This allows us to consider the variation of dimensionless parameters: normalized ion, $R/L_{T_{\rm{i}}}$, and electron, $R/L_{T_{\rm e}}$, temperature gradients, temperature ratio $T_{\rm e}/T_{\rm{i}}$, normalized electron density gradient $R/L_{n_{\rm e}}$, electron–ion, $\nu_{\rm {ei}}^{\ast}$, and ion–ion, $\nu_{\rm {ii}}^{\ast}$, collisionalities. To study the dependencies on them, a normalized anomalous ion heat flux $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ is used as the transport characteristics. It is shown that high or low $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$ formation is mostly distinguished by three of the parameters: $T_{\rm e}/T_{\rm{i}}$, $R/L_{n_{\rm e}}$, and $\nu_{\rm {ii}}^{\ast}$:

(1) Combination of high $T_{\rm e}/T_{\rm{i}}$, high $\nu_{\rm {ii}}^{\ast}$, and $R/L_{n_{\rm e}}=6$–10 results in high values of normalized anomalous ion heat fluxes $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$.

(2) Combination of low $T_{\rm e}/T_{\rm{i}}$ and low $\nu_{\rm {ii}}^{\ast}$ (together with $R/L_{n_{\rm e}}>10$) or high $\nu_{\rm {ii}}^{\ast}$ (together with $R/L_{n_{\rm e}}<6$) results in low values of normalized anomalous ion heat fluxes $Q_{\rm{i}}^{\rm {an}}/(n_{\rm{i}} T_{\rm{i}})$.

In order to investigate which parameter is dominant and which turbulent processes are responsible for the observed dependencies, first-principle modeling is required. It is an ongoing work, and the results will be published elsewhere.