| Citation: | Peng DENG, Wenzhe MAO, Zhipeng CHEN, Yinan ZHOU, Peng SHI, Zhoujun YANG, Li GAO, Tao LAN, Jinlin XIE, Hong LI, Zian WEI, Adi LIU, Chu ZHOU, Weixing DING, Wandong LIU, Ge ZHUANG. The impact of toroidal mode coupling on high-density discharges in J-TEXT[J]. Plasma Science and Technology, 2024, 26(12): 125101. DOI: 10.1088/2058-6272/ad659f |
Density limit has long been a widely studied issue influencing the operating range of tokamaks. The rapid growth of the m/n = 2/1 (where m and n are poloidal and toroidal mode numbers, respectively) tearing mode is generally regarded as a primary precursor to the density limit disruption. In this experiment, the coupling of the m/n = 1/1 mode and the m/n = 2/1 mode in high-density plasma was observed. During a sawtooth cycle, the frequencies of the two modes gradually converge until they become equal. After that, toroidal coupling occurs between the 1/1 and 2/1 modes, resulting in a mutually fixed phase relationship. With the occurrence of toroidal coupling, the 2/1 mode is stabilized. Prior to the disruption, the cessation of the 1/1 and 2/1 mode coupling, along with the rapid growth in the amplitude of the 2/1 mode, can be observed. Additionally, under the same parameters, comparing discharges with or without the 1/1 mode, it is found that the presence of the 1/1 mode leads to higher plasma density and temperature parameters.
The phenomenon of the density limit is widely observed in various toroidal magnetic confinement fusion devices, which can impose severe constraints on the safe operation region, as evidenced by numerous experiments, especially the results on tokamaks [1]. Attempts to increase plasma density beyond a certain threshold, known as the Greenwald density limit nG=Ip/πa2 ((1020 m−3), where Ip is the plasma current (MA) and a is the minor radius (m)), have been shown to induce various instabilities in the internal plasma dynamics, leading to enhanced transport or even disruptions [2]. Previous experiments have revealed the dominant role of m/n = 2/1 mode in this process [3].
One of the typical characteristics of density limit disruption is the combined instabilities of m = 1 and m = 2 modes, with observations of mode co-growth in many experiments [4, 5]. Extensive theoretical analyses have been conducted on the “m = 1 erosion” of the plasma core observed during density limit disruption in TFTR [6]. Analysis of ECE signals on TFTR suggests that m = 1 erosion is attributed to the formation of cold plasma bubbles penetrating into the plasma core. Similar m = 1 perturbations have also been observed in smaller tokamak devices like LT-4 [7]. In small size tokamaks, m = 1 perturbations gradually grow before disruption and are typically coupled with m = 2 modes (i.e., m = 1 and m = 2 modes rotating at the same frequency and in the same direction) [4, 5].
One explanation for the density limit involves large m = 1 kink mode transporting cold plasma bubbles from the edge to the core, resulting in the formation of a hollow current density distribution and the instability of the m/n = 2/1 mode [8]. This model describes the typical features of density limit disruption in TFTR plasma, including the presence of m = 1 cold bubble and the eventual instability of the m/n = 2/1 mode [6]. Another possible disruption mechanism is related to the combined growth of internal modes with different helicities in toroidal plasmas [9]. The growth of coupled perturbations among different modes, mainly m/n = 1/1, 3/2, and 2/1 modes, disrupts the isolated magnetic surfaces between q = 1 and q = 2 islands, leading to sudden cooling of the plasma core (thermal quench). This model describes most of the features of density limit disruption observed in JET [9] and other tokamaks [7].
In toroidal magnetically confined plasmas, m/n modes can induce (m±1)/n magnetic perturbation (MP) due to toroidicity effect [10]. Once additional tearing modes (TM) are formed, two TMs may mutually destabilize and enhance each other through toroidal coupling. This effect has been theoretically and numerically studied [11–13]. The overlap of TM magnetic islands has been considered as a plausible model for the disruption mechanism [14, 15]. For instance, the coupling between 2/1 and 3/1 modes can result in mutual destabilization or even major disruptions [16]. However, observations on KSTAR [17] have shown competition between radially adjacent TMs rather than mutual promotion, resulting in few magnetic islands to survive and playing the dominant role. Guo et al [18] applied a resistive magnetohydrodynamics (MHD) model to investigate the impact of sawtooth on classical/neoclassical TMs in tokamak plasmas. The results indicated that the m = 2 mode can be driven by the m = 1 mode. The growth rate of TMs through toroidal coupling depends on the inverse aspect ratio ε in the linear phase. Reference [19] suggests that TMs can be stabilized by short-period sawtooth oscillations, where current oscillations and the induced electric field due to rapid changes in current play a crucial role in TM stabilization. The results indicate that the 2/1 component of the mode decays due to the unstable resistive 1/1 mode. Reference [20] used experimental equilibrium reconstructions in the DIII-D tokamak to examine the magnetohydrodynamic and two-fluid growth rates of m/n = 2/1 TM in the presence of well-separated central sawtooth oscillations. Simulation results demonstrate that the coupling of 2/1 mode with other ones can be significant even at low β. For high density discharge, current and pressure profiles may evolve violently, where coupling among various modes can play a crucial role in disruptions. Currently, there is no unified conclusion regarding the outcomes resulting from toroidal coupling between modes (stabilization or destabilization of tearing modes). Here, we aim to investigate the detailed process of mode coupling and its influence on the stability of tearing modes experimentally on J-TEXT. Additionally, we seek to demonstrate its potential benefits for operating high-density plasma discharges.
This article reports the interaction between the 1/1 and 2/1 modes observed prior to density limit disruption on J-TEXT. The results indicate that the primary interaction between modes manifests as toroidal coupling. When the two modes undergo toroidal coupling, they synchronize in frequency, lock phase, and the m = 2 mode becomes stabilization. Toroidal coupling stabilizes the 2/1 mode initially, but once the density hits a certain threshold, the decoupling from the 1/1 mode triggers a rapid amplification of the 2/1 mode, culminating in a significant disruption.
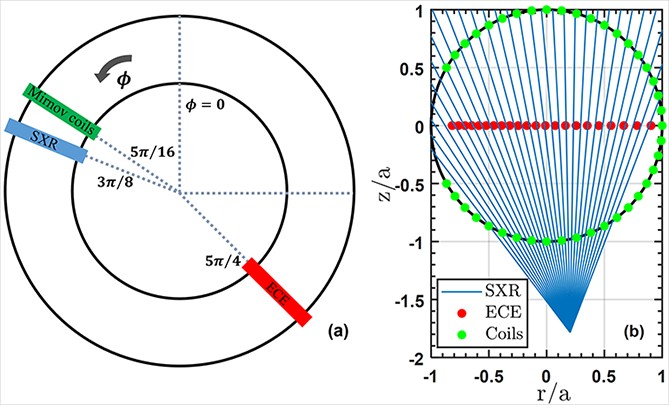
J-TEXT [21–24] is a medium-sized tokamak with a circular cross-section, featuring a major radius of 1.05 m and a minor radius of 0.255 m. The diagnostics primarily used in this experiment include soft X-ray (SXR), interferometer system, electron cyclotron emission (ECE), and boundary magnetic probes, as shown in figure 1 [25–28]. The SXR measures the line integral of soft X-ray radiation with 2 μs temporal resolution. The radiation with an energy below 300 eV is filtered by a 12 μm thick beryllium film. The ECE system provides the local relative electron temperature and the corresponding fluctuations, ranging from r/a = −0.82 to 0.9 in the midplane when BT = 1.79 T. The spatial resolution of ECE is ~ 1.25 cm, and temporal resolution is 1 μs. From these diagnostics, we can obtain information about plasma density, relative electron temperature, and magnetic perturbations.
To elucidate the dynamics and facilitate the understanding of density limit disruptions during different phases, different discharge parameters are scanned to explore the characteristics of MHD activities during disruption trigged by high density. Here, toroidal magnetic field BT is fixed with different flat-top plasma current values, which means that the edge safety factors or their profiles are different. For each discharge, plasma density is rising slowly using density control until disruption [29].
A typical Ohmic discharge on J-TEXT is shown in figure 2 with shot #1063484. The main plasma parameters during the current flat-top are plasma current Ip = 100 kA, toroidal field BT = 1.79 T, edge safety factor qa ≈ 4.8 and maximum central line-averaged density ¯ne≈3.55×1019 m−3≈0.7nG (where nG is the Greenwald density limit). It is shown from the edge Mirnov signals that magnetic fluctuation amplitude increases continually with the density and bursts while approaching disruption. Electron temperature decreases with enhanced fluctuation amplitude from ECE signal. SXR signal also indicates increasing fluctuation before disruption, and the rise of overall emission level, which is probably related with steadily rising electron density. After the disruption triggered at about 490 ms, plasma confinement deteriorates due to strong MHD activities.
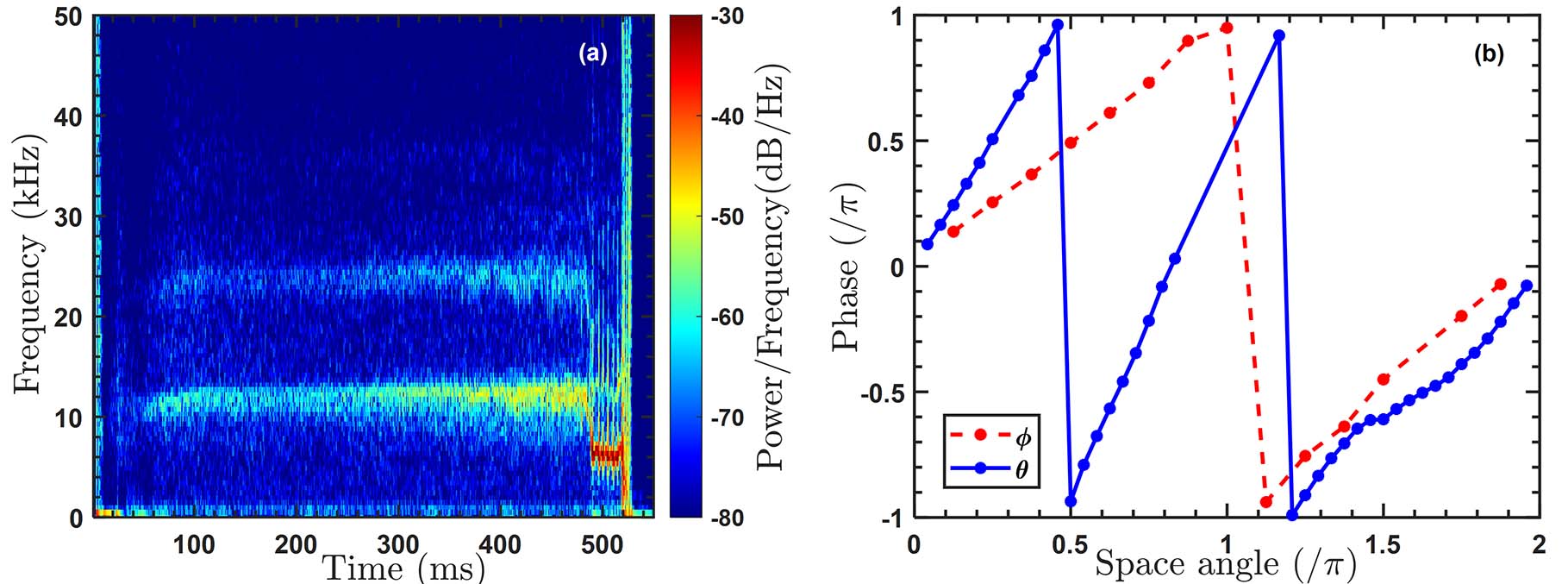
A frequency of approximately 12 kHz mode is shown in the spectrum of Mirnov coil signal, as shown in figure 3(a). Through correlation analysis of magnetic probe signals [30], we can determine the phase of different poloidal and toroidal positions of the probes, as shown in figure 3(b), indicating that the dominant MHD mode is m/n = 2/1 [31]. Figure 4(a) displays the time-frequency spectrogram of the ECE signal in the core region, indicating periodically occurring modes around 10 kHz, which is not observed by Mirnov coils at the edge. Figure 4(b) shows the cross-correlation coefficients and phase differences between other ECE signals and the core ECE one around 10 kHz. It can be observed that the perturbation around 10 kHz is concentrated in the plasma core, and there is a phase reversal in the core. Based on the characteristic periodic collapses of the sawtooth, it is inferred that this mode corresponds to the internal 1/1 instability. From the signals of the magnetic probes, it is shown that as the density increases, the amplitude of the m/n = 2/1 mode gradually grows. Simultaneously, the magnetic and temperature fluctuation signals exhibit high-frequency branches while approaching high density limit, indicating steeper profile gradient or possible mode coupling near the resonance surface.
The spatial distributions of the two modes can be provided by an equilibrium reconstruction procedure (ERP) [32]. Figure 5(a) displays the q profiles at different times, revealing a continuous increase in q shear near q = 2. Additionally, the magnetic island width can be calculated by combining the q profiles provided by ERP with the edge Mirnov signals. The analytical relationship between magnetic island width and magnetic perturbations profile can be derived using linear MHD model, expressed by the formula w∝√ Bθ(rc), where Bθ is the perturbation of poloidal magnetic and rc is the radius corresponding to Mirnov coils location [33]. As shown in figure 5(b), the distances between the q = 1 and q = 2 magnetic surfaces as well as the width of the m/n = 2/1 magnetic island are illustrated at different times. It can be observed that the width of the 2/1 magnetic island continuously increases, with a rapid surge just before disruption occurs. Additionally, there is no significant change in the distance between the q = 1 and q = 2 surfaces. During the current flat-top phase from 200 ms to 490 ms, noticeable sawtooth oscillations are observed in the SXR and ECE signals. Therefore, as the density increases, the interaction between the two modes will gradually strengthen, which may lead to strong mode coupling.
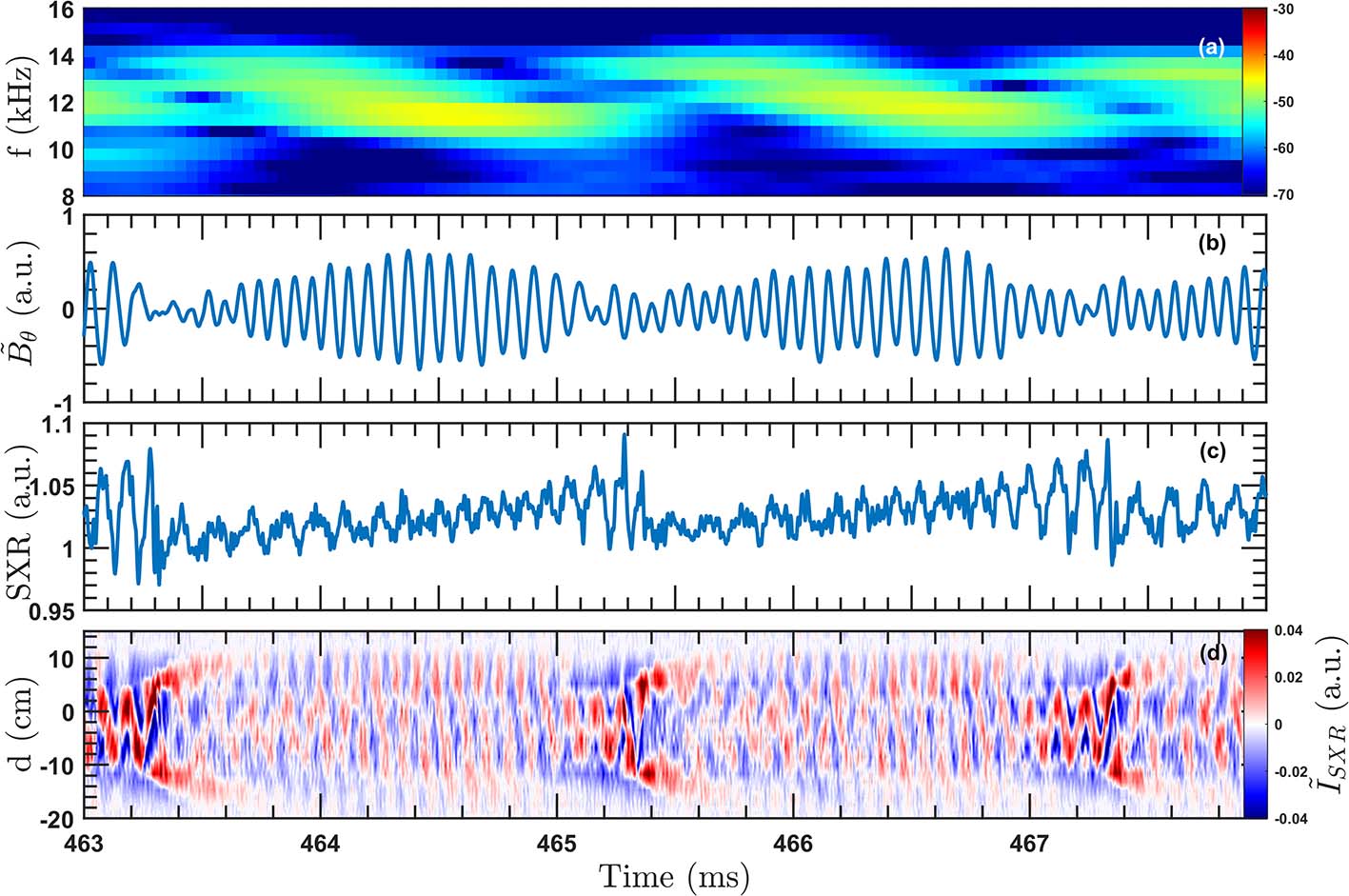
To investigate the possible mode coupling effect more in detail, we analyzed the correlation of different modes in one sawtooth cycle. At high densities (0.6nG–0.7nG), it is observed that the amplitude of the 2/1 mode is modulated by the sawtooth activities, as shown in figure 6. It can be seen that after each sawtooth collapse, the amplitude of the 2/1 mode gradually increases, while the frequency slightly decreases. Additionally, there is a lower frequency, which happens to be close to the frequency of the 1/1 mode. The amplitude of the 2/1 mode reaches its maximum value approximately half sawtooth period. In the later half sawtooth period, the amplitude of the 2/1 mode gradually decreases, reaching its minimum value almost at the time of sawtooth crash. With the crash of the next sawtooth, the 2/1 mode begins to increase again, and this cycle repeats. It can be seen that there is a strong correlation between the sawtooth and the 2/1 mode, and the amplitudes of the m/n = 1/1 and m/n = 2/1 modes are negative. That is, before the sawtooth collapse, the m/n = 1/1 mode is stronger while the m/n = 2/1 mode is weaker, whereas in the middle of the sawtooth period, the situation is exactly the opposite. This characteristic can also be observed from the SXR signal, as shown in figure 6(d), which displays a contour plot of the SXR perturbations. It can be observed that the amplitude of the 1/1 mode is the strongest before the sawtooth collapse, while during the mid-period of the sawtooth, the 2/1 mode predominates. On one hand, this shot is a low beta discharge since it is a pure Ohmic discharge. This suggests that the modulation of the 2/1 mode by the sawtooth is not primarily caused by the change in the pressure profile due to the 1/1 mode [20]. On the other hand, it can be seen that the amplitude of the 2/1 mode is directly related to the amplitude of the 1/1 mode (rather than to the sawtooth collapse). This can be observed from the fact that the reduction in the amplitude of the 2/1 mode occurs during the half sawtooth cycle rather than sawtooth collapse. In conclusion, the most critical factor here is the interaction between the 1/1 and 2/1 modes.
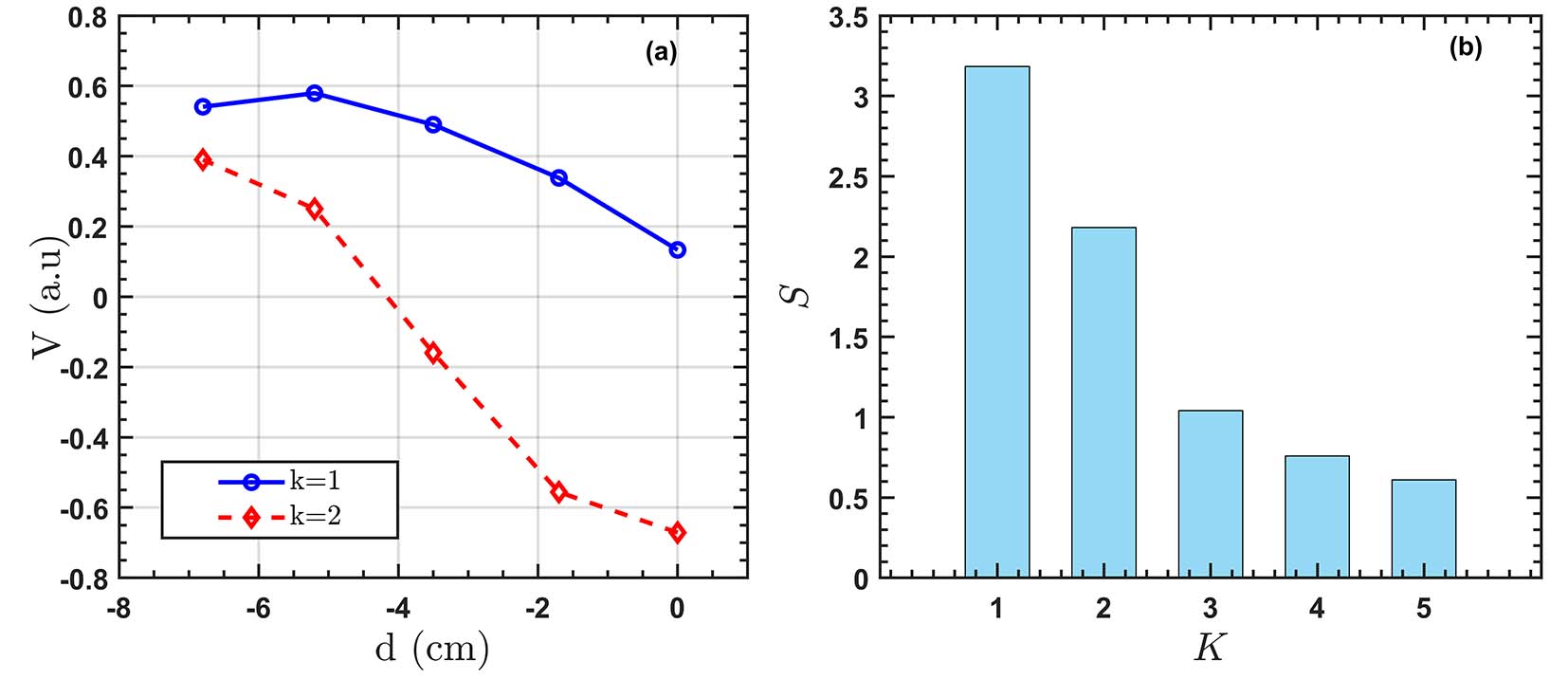
One of the most prominent features of toroidal coupling is the mutual locking of mode phases [34]. The phase of the 2/1 mode can be easily obtained from the magnetic probe signal, while the 1/1 mode is difficult to directly extract from the ECE or SXR signals because its amplitude is relatively small during the half sawtooth cycle when the amplitude of the 2/1 mode is large. Due to the different spatial characteristics exhibited by m = 2 and m = 1 in the core region, singular value decomposition (SVD) [35] is employed here to analyze the SXR signal inside the q = 1 surface.
As shown in figure 7, the results of SVD on the core SXR perturbation signal indicate that the first two values correspond to signals with m = 2 and m = 1, respectively, with the first two values dominating (~ 70%) based on the spatial eigenvalues. For the perturbation signal of the poloidal magnetic probe, the maximum values represent the O-point, while the minimum values represent the X-point. However, for the SXR perturbations, the minimum values represent the passage of the O-point through its chord, while the maximum values represent the passage of the X-point through its chord [36]. Due to the negative spatial eigenvalue at d = 0, for the low-field side, the maximum values of the perturbation signal corresponding to m = 1 obtained from SVD represent the O-point, while the minimum values represent the X-point. Using the m = 1 signal obtained from SVD and comparing it with the poloidal magnetic perturbation signal on the low-field side, the results are shown in figure 8. It can be observed that within one sawtooth period, the frequencies of the two signals gradually approach each other. When the frequencies are equal, the two signals undergo toroidal coupling. At this point, the phases of both signals on the low-field side are consistent (both at the O-point or X-point). These observations are consistent with the characteristics of toroidal coupling. When toroidal coupling first occurs, the amplitude of the m = 2 mode reaches its maximum. Subsequently, with the onset of toroidal coupling, the amplitude of the m = 2 mode gradually decreases, indicating stabilization of the m = 2 mode. This is consistent with the conclusion obtained in reference [36] using computer tomography inversion reconstruction.
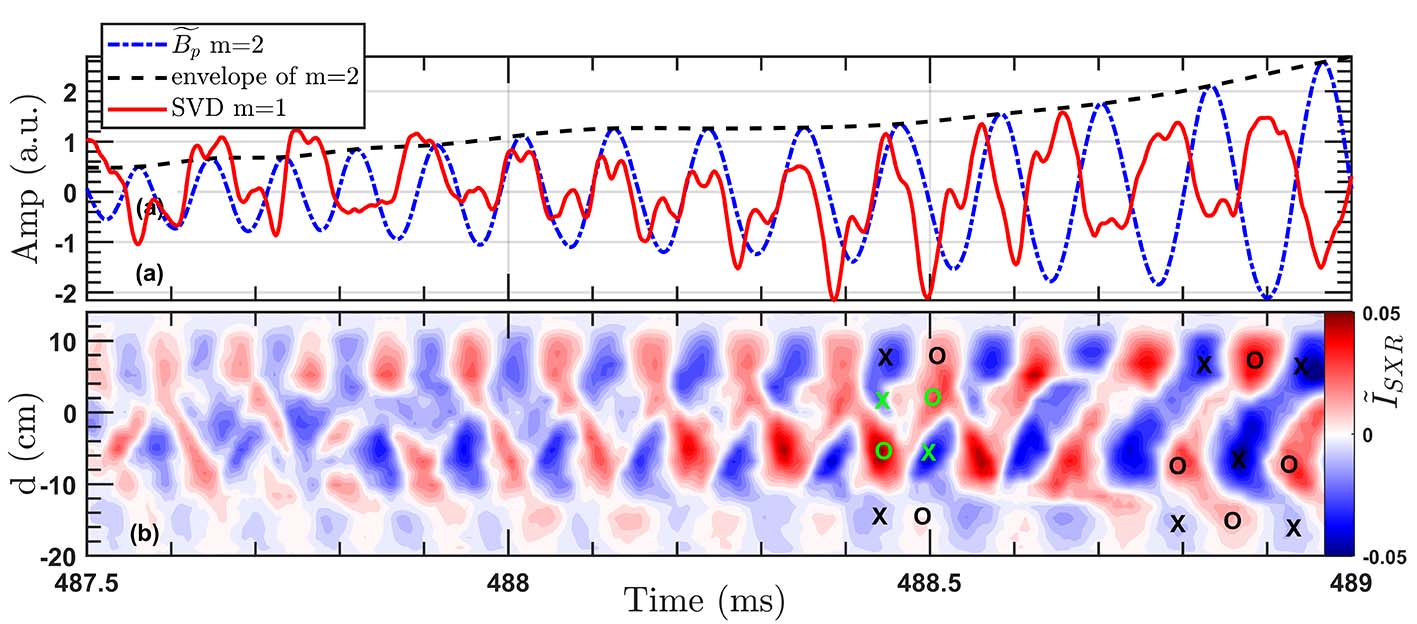
We noticed that before the occurrence of the first minor disruption, there was a “supposed” sawtooth crash around 488.7 ms (sawtooth period ~ 2 ms), but ultimately this sawtooth did not collapse because we can still observe the presence of the 1/1 mode in the core region. From figure 9(a), we can observe that the SVD data confirm the toroidal coupling between the 1/1 mode and the 2/1 one (488–488.5 ms). This result leads to a plateau period in the growth of the m = 2 mode amplitude before the occurrence of the minor disruption. Since both modes have relatively large amplitudes at this time, they can be clearly observed simultaneously in the SXR contour plot in figure 9(b).
To demonstrate the observed phenomenon of mode toroidal coupling in experiments visually, we simulated the evolution of the SXR signal with the rotating magnetic islands. Figure 10(a) depicts the distribution of assumed equilibrium magnetic surfaces and corresponding chords of the SXR array, where the poloidal plane is divided into 36 regions by 35 magnetic surfaces. The dashed lines represent the q = 1 and q = 2 magnetic surfaces, with normalized radii of r1 = 0.26 and r2 = 0.62, respectively (the position distribution here is based on experimental data). Figure 10(b) illustrates the phase relationship between the two modes at time zero. Figure 10(c) shows the distribution of the normalized unit volume element radiation value, iSXR, between different magnetic surfaces. The plateau observed in the middle region corresponds to the m = 2 magnetic island regions. The value for each region is calculated based on the central radius of the corresponding region of the equilibrium magnetic surface. The value corresponding to the m = 2 magnetic island region is calculated based on the radius corresponding to q = 2 of the equilibrium magnetic surface. Here, it is assumed that the density and temperature distributions follow a simple form:
| ne=ne0(1−r2/a2)2, | (1) |
| Te=Te0(1−r2/a2)2. | (2) |
For simplicity in calculation, we only consider the bremsstrahlung component and ignore the effects brought by impurities. The radiation signal of the SXR per unit volume is:
| iSXR ∼ n2eT1/2e. | (3) |
Assuming equal solid angles for each detector, the total radiation for a single chord would be:
| ISXR ∼ ∑l2iSXRdl. | (4) |
Here l represents the distance from the radiation element to the detector, and constant factors are neglected. The regions within q = 1 surface and those affected by the m = 2 magnetic islands are set with step angles of w1 = 16° and w2 = 8°, respectively. By integrating the radiation values along the path of each SXR chord for each time slice, the simulated SXR signal under the presence of rotating magnetic islands can be obtained.
The experimental and simulation results are shown in figures 11(a) and (b) respectively. It can be observed that the experimental phenomena are reproduced quite well, indicating that the coupling between the two modes conforms to the phase relationship observed in the toroidal coupling phenomenon mentioned earlier.
The results above demonstrate that in high-density discharges with sawtooth, there is an interaction between the m = 1 and m = 2 modes through toroidal coupling. This is evidenced by the modulation of the m = 2 mode amplitude by the sawtooth period and the negative correlation between the amplitudes of the m = 2 and m = 1 modes. Consequently, during the presence of sawtooth, the amplitude of the 2/1 mode does not increase significantly. It is worth noting that even after the disappearance of sawtooth, the two modes continue to exhibit toroidal coupling. However, once the toroidal coupling ends, the 2/1 mode undergoes rapid growth, leading to minor disruptions. As shown in figure 12, under the same discharge parameters (Ip = 140 kA, BT = 1.79 T), there are significant differences from sawtooth. When sawtooth is present, the plasma density and temperature are higher compared to the case without sawtooth. Additionally, the amplitude of the 2/1 mode remains at a relatively low level before the small disruption when sawtooth is present.
On J-TEXT, we observed that at high densities, the amplitude of the 2/1 mode is significantly modulated by the sawtooth period. Further analysis using SVD on the SXR signals within the q = 1 surface revealed the phase of modes. The interaction between the 1/1 and 2/1 modes at high densities exhibits characteristics of toroidal coupling effect. The toroidal coupling between the two modes suppressed the growth of the 2/1 mode, leading to its temporary stabilization. Additionally, we observed the disappearance of the sawtooth crash before minor disruptions, while the remaining steady 1/1 mode still exhibited the same toroidal coupling effect with the 2/1 mode. Further, by simulating the SXR signal, we reproduced the experimental phenomenon and confirmed the mutual coupling between the two modes at this point.
During the presence of sawtooth, the spontaneously generated 1/1 kink mode grows largely enough. Due to toroidal coupling, it stabilizes the 2/1 tearing mode, preventing significant growth in its amplitude. Without toroidal coupling, rapid growth of the 2/1 mode follows, routinely leading to the occurrence of a minor disruption. This suggests that an intrinsic fluctuation of m/n = 1/1 or an external perturbation [37, 38] could appropriately delay or mitigate the high-density disruptions caused by rapid growth of 2/1 instability.
The authors would like to express their deepest gratitude to the J-TEXT team for their invaluable support and assistance. This work was supported by National Natural Science Foundation of China (Nos. 12175227 and 51821005), the Fundamental Research Funds for the Central Universities (No. USTC 20210079), and the Collaborative Innovation Program of Hefei Science Center, CAS (No. 2022HSC-CIP022).
| [1] |
Greenwald M 2002 Plasma Phys. Control. Fusion 44 R27 doi: 10.1088/0741-3335/44/8/201
|
| [2] |
Greenwald M et al 1988 Nucl. Fusion 28 2199 doi: 10.1088/0029-5515/28/12/009
|
| [3] |
Vershkov V A and Mirnov S V 1974 Nucl. Fusion 14 383 doi: 10.1088/0029-5515/14/3/012
|
| [4] |
Sauthoff N R, Von Goeler S and Stodiek W 1978 Nucl. Fusion 18 1445 doi: 10.1088/0029-5515/18/10/012
|
| [5] |
Equipe T F R 1975 Nucl. Fusion 15 1053 doi: 10.1088/0029-5515/15/6/011
|
| [6] |
Fredrickson E D et al 1993 Nucl. Fusion 33 1759 doi: 10.1088/0029-5515/33/12/I01
|
| [7] |
Howard J and Persson M 1992 Nucl. Fusion 32 361 doi: 10.1088/0029-5515/32/3/I02
|
| [8] |
Kleva R G and Drake J F 1991 Phys. Fluids B 3 372 doi: 10.1063/1.859747
|
| [9] |
Bondeson A et al 1991 Nucl. Fusion 31 1695 doi: 10.1088/0029-5515/31/9/008
|
| [10] |
Hegna C C, Callen J D and LaHaye R J 1999 Phys. Plasmas 6 130 doi: 10.1063/1.873265
|
| [11] |
Carreras B et al 1980 Phys. Fluids 23 1811 doi: 10.1063/1.863206
|
| [12] |
Fitzpatrick R et al 1993 Nucl. Fusion 33 1533 doi: 10.1088/0029-5515/33/10/I11
|
| [13] |
Li D and Huo Y P 1993 Phys. Fluids B: Plasma Phys. 5 3737 doi: 10.1063/1.860844
|
| [14] |
Stix T H 1976 Phys. Rev. Lett. 36 521 doi: 10.1103/PhysRevLett.36.521
|
| [15] |
Finn J M 1977 Phys. Fluids 20 1749 doi: 10.1063/1.861776
|
| [16] |
He Y et al 2023 Plasma Phys. Control. Fusion 65 035012 doi: 10.1088/1361-6587/acb00f
|
| [17] |
Kim G et al 2018 Plasma Phys. Control. Fusion 60 035009 doi: 10.1088/1361-6587/aaa2eb
|
| [18] |
Guo W P et al 2016 Phys. Plasmas 23 062117 doi: 10.1063/1.4953900
|
| [19] |
Yang X Q and Zhou D 2018 Phys. Plasmas 25 112504 doi: 10.1063/1.5054701
|
| [20] |
Brennan D P and Sugiyama L E 2006 Phys. Plasmas 13 052515 doi: 10.1063/1.2202133
|
| [21] |
Zhuang G et al 2011 Nucl. Fusion 51 094020 doi: 10.1088/0029-5515/51/9/094020
|
| [22] |
Zhuang G et al 2017 Nucl. Fusion 57 102003 doi: 10.1088/1741-4326/aa6009
|
| [23] |
Liang Y et al 2019 Nucl. Fusion 59 112016 doi: 10.1088/1741-4326/ab1a72
|
| [24] |
Zhuang G et al 2009 Plasma Sci. Technol. 11 439 doi: 10.1088/1009-0630/11/4/14
|
| [25] |
Li J C et al 2014 Rev. Sci. Instrum. 85 11E414 doi: 10.1063/1.4886432
|
| [26] |
Yang Z J et al 2016 Rev. Sci. Instrum. 87 11E112 doi: 10.1063/1.4960167
|
| [27] |
Chen J et al 2014 Rev. Sci. Instrum. 85 11D303 doi: 10.1063/1.4891603
|
| [28] |
Han D L et al 2021 Plasma Sci. Technol. 23 055104 doi: 10.1088/2058-6272/abeeda
|
| [29] |
Ke X et al 2016 Plasma Sci. Technol. 18 211 doi: 10.1088/1009-0630/18/2/20
|
| [30] |
Harley T R et al 1989 Nucl. Fusion 29 771 doi: 10.1088/0029-5515/29/5/007
|
| [31] |
Huang M X et al 2016 Plasma Phys. Control. Fusion 58 125002 doi: 10.1088/0741-3335/58/12/125002
|
| [32] |
Chen J et al 2014 Rev. Sci. Instrum. 85 103501 doi: 10.1063/1.4896476
|
| [33] |
Salzedas F et al 2002 Phys. Rev. Lett. 88 075002 doi: 10.1103/PhysRevLett.88.075002
|
| [34] |
Equipe T F R 1977 Nucl. Fusion 17 1283 doi: 10.1088/0029-5515/17/6/015
|
| [35] |
Nardone C 1992 Plasma Phys. Control. Fusion 34 1447 doi: 10.1088/0741-3335/34/9/001
|
| [36] |
Yoshimura S, Maekawa T and Terumichi Y 2002 Phys. Plasmas 9 3378 doi: 10.1063/1.1486449
|
| [37] |
Li J C et al 2017 Plasma Phys. Control. Fusion 59 085005 doi: 10.1088/1361-6587/aa726c
|
| [38] |
Ding Y H et al 2018 Plasma Sci. Technol. 20 125101 doi: 10.1088/2058-6272/aadcfd
|
| [1] | Yiming ZU, Zhiwei MA, Yuchen XU. Magnetohydrodynamic simulation study of impurity radiation-excited and driven tearing mode[J]. Plasma Science and Technology, 2025, 27(3): 035102. DOI: 10.1088/2058-6272/ad9e91 |
| [2] | Yi Zhang, Tao Xu, Wen Wang, Fang Gang, Nengchao Wang. The influence of RF-current to tearing mode in multi-harmonic theory[J]. Plasma Science and Technology. DOI: 10.1088/2058-6272/adcefd |
| [3] | Yinan ZHOU, Ge ZHUANG, Peng SHI, Li GAO, Zhoujun YANG, Xiaoqing ZHANG, the J-TEXT Team. Observation of the poloidally asymmetrical density perturbation of sawtooth collapse on J-TEXT[J]. Plasma Science and Technology, 2023, 25(3): 035101. DOI: 10.1088/2058-6272/ac9346 |
| [4] | Yan CHAO, Wei ZHANG, Liqun HU, Kangning GENG, Liqing XU, Tao ZHANG, Qing ZANG, Tianfu ZHOU. Observations of mode frequency increase and the appearance of ITB during the m/n = 1/1 kink mode in EAST high electron temperature long pulse operation[J]. Plasma Science and Technology, 2023, 25(2): 025107. DOI: 10.1088/2058-6272/ac92d0 |
| [5] | Wei ZHANG, Zhiwei MA, Haowei ZHANG, Xin WANG. Sawtooth-like oscillations and steady states caused by the m/n = 2/1 double tearing mode[J]. Plasma Science and Technology, 2022, 24(3): 035104. DOI: 10.1088/2058-6272/ac4bb4 |
| [6] | Zhenghao REN (任政豪), Jinyuan LIU (刘金远), Feng WANG (王丰), Huishan CAI (蔡辉山), Zhengxiong WANG (王正汹), Wei SHEN (申伟). Influence of toroidal rotation on the tearing mode in tokamak plasmas[J]. Plasma Science and Technology, 2020, 22(6): 65102-065102. DOI: 10.1088/2058-6272/ab77d4 |
| [7] | Weikang TANG (汤炜康), Lai WEI (魏来), Zhengxiong WANG (王正汹), Jialei WANG (王佳磊), Tong LIU (刘桐), Shu ZHENG (郑殊). Effects of resonant magnetic perturbation on locked mode of neoclassical tearing modes[J]. Plasma Science and Technology, 2019, 21(6): 65103-065103. DOI: 10.1088/2058-6272/ab0a18 |
| [8] | Ding LI (李定), Wen YANG (杨文), Huishan CAI (蔡辉山). On theoretical research for nonlinear tearing mode[J]. Plasma Science and Technology, 2018, 20(9): 94002-094002. DOI: 10.1088/2058-6272/aabde4 |
| [9] | CHEN Yebin(陈晔斌), HU Liqun(胡立群), CHEN Kaiyun(陈开云), LI Miaohui(李妙辉). Study of Inverted Sawtooth Activities in EAST Plasma[J]. Plasma Science and Technology, 2014, 16(3): 188-192. DOI: 10.1088/1009-0630/16/3/03 |
| [10] | Liu Zixi (刘子奚), Gao Xiang (高翔), Jie Yinxian (揭银先), Ding Bojiang (丁伯江), Yang Yao (杨曜), HT- team, EAST team. Sawtooth control experiments on HT-7 and EAST tokamak[J]. Plasma Science and Technology, 2012, 14(4): 278-284. DOI: 10.1088/1009-0630/14/4/03 |