Alfvén continuum in the presence of a magnetic island in a cylinder configuration

Junhui YANG; Jinjia CAO; Jianhua ZHAO; Yongzhi DAI; Dong XIANG

doi:10.1088/2058-6272/ac9de0

Plasma Science and Technology > 2023 > 25(3): 035102. > DOI: 10.1088/2058-6272/ac9de0

Junhui YANG, Jinjia CAO, Jianhua ZHAO, Yongzhi DAI, Dong XIANG. Alfvén continuum in the presence of a magnetic island in a cylinder configuration[J]. Plasma Science and Technology, 2023, 25(3): 035102. DOI: 10.1088/2058-6272/ac9de0

Citation:

PDF (1754 KB)

Alfvén continuum in the presence of a magnetic island in a cylinder configuration

School of Nuclear Science and Technology, University of South China, Hengyang 421001, People's Republic of China

More Information

Corresponding author:
Jinjia CAO, E-mail: caojinjia@usc.edu.cn
Received Date: June 19, 2022
Revised Date: October 19, 2022
Accepted Date: October 25, 2022
Available Online: December 06, 2023
Published Date: January 17, 2023

Graphical Abstract

Abstract

Abstract

In this work, the effect of a magnetic island on Alfvén waves is studied. A physical model is established wherein Alfvén waves propagate in the presence of a magnetic island in a cylindrical geometry. The structure of the Alfvén wave continuum is calculated by considering only the coupling caused by the periodicity in the helical angle of the magnetic island. The results show that the magnetic island can induce an upshift in the Alfvén continuum. Moreover, the coupling between different branches of the continuous spectrum becomes more significant with increasing continuum mode numbers near the boundary of the magnetic island.
- Alfvén waves,
- cylindrical geometry,
- magnetic island,
- continuum coupling

FullText(HTML)

1. Introduction

Alfvén waves physics is an important subject in plasma physics, especially the continuum gap of Alfvén waves in magnetic confinement fusion plasma, which can indicate the possible locations of discrete Alfvén eigenmodes and induce fast ion losses [1]. In burning plasmas, a large number of energetic particles can interact with Alfvén waves and induce different types of Alfvén global eigenmodes, such as toroidicity-induced Alfvén eigenmodes [2–4] and beta-induced Alfvén eigenmodes (BAE) [5–7]. Waves and particles interact non-linearly, which may lead to a redistribution or even to a loss of energetic particles. This poses a serious threat to the operation safety of magnetic confinement devices. Recently, the interaction between magnetic islands and Alfvén waves has attracted extensive attention. In EAST (the Experimental and Advanced Superconducting Tokamak), it has been observed that BAEs are driven when the magnetic island width exceeds a threshold value, and that the BAE frequencies will increase with the magnetic island width [8]. Similar phenomena were also observed in FTU [9, 10] and TEXTOR [11]. In TJ-II [12], it was observed that magnetic islands can significantly change the frequency of the gap locations in the continuous Alfvén spectrum. Biancalani et al analyzed the influence of magnetic islands on the Alfvén continuum spectrum and found that continuum gaps formed owing to the ellipticity of the magnetic island and determined the frequency of the shifted continuum [13–15]. Cook and Hegna solved the ideal magnetohydrodynamics (MHD) equation via WKB approximation (Wenzel–Kramers–Brillouin approximation), and they determined the influence of magnetic islands on the shear Alfvén continuum. Their results show that magnetic islands can change the frequencies of the shear Alfvén continuum [16]. Subsequently, magnetic-island-induced Alfvén eigenmodes were observed by adding magnetic islands to the Madison symmetry ring of the inverse field hoop device and injecting a neutral beam injection, and magnetic islands cause a significant upward frequency shift of the Alfvén wave continuum [17].

In this work, a cylindrical geometry is adopted. Thus, the period $N_{p} = 1 .$ We use a W7-X like model, i.e. a cylinder with the major radius $R_{0} \approx 5.5 m,$ the minor radius $a \approx 0.55 m$ and an appropriate value for $ι .$ The continuous Alfvén spectrum is studied in the presence of a magnetic island. The Alfvén continua inside and outside the magnetic island are calculated. Due to the symmetry of the cylinder configuration, only the inhomogeneity due to the magnetic island for creating gaps in the shear Alfvén continuum is considered. Our results are consistent with the previous numerical results of Biancalani et al [13–15] and Cook et al [16, 17]. Moreover, we found that an obvious coupling occurs between the Alfvén continua of different mode numbers near the magnetic island separatrix, but the frequency of the continuum significantly shifts, and the coupling far away from the magnetic island is not obvious.

This paper is organized as follows. In section 2, the magnetic field geometry is introduced. In section 3, the equations for the shear Alfvén wave continuum are discussed. In section 4, the numerical results are provided. Finally, the discussion and the summary are given in section 5.

2. Island coordinate system

For magnetic confinement devices with a large inverse aspect-ratio ( $ε = r / R_{0} ≪ 1$ ), such as W7-X stellarator, the coordinate system $(r, θ, φ)$ can be regarded as a cylindrical geometry, wherein $r$ is the minor radius, $θ$ is the poloidal angle, and $φ$ is the toroidal angle. The equilibrium magnetic field is

$\vec{B} = \frac{B_{0}}{R_{0}} r^{2} ι \nabla θ + R_{0} B_{0} \nabla φ,$

(1)

where $ι$ is the rotational transform, which is the reciprocal of $q .$ $R_{0}$ and $B_{0}$ are the major radius and magnetic field, respectively. Next, we introduce a magnetic island generated by a magnetic perturbation of the form:

$\tilde{ψ} = A \cos (M θ + N φ),$

(2)

${\vec{B}}_{1} = \nabla \times (\tilde{ψ} {\vec{B}}_{0}),$

(3)

where $A$ is the perturbation amplitude, $M$ and $N$ are the poloidal and toroidal mode numbers of the magnetic island, respectively. Then, the perturbed magnetic field can be written as

$\begin{matrix} {\vec{B}}_{1} = (\frac{B_{0}}{r} \frac{\partial \tilde{ψ}}{\partial θ} - \frac{B_{0}}{R_{0}} \frac{r}{R_{0}} ι \frac{\partial \tilde{ψ}}{\partial φ}) \frac{\partial \vec{r}}{\partial r} + \tilde{ψ} \frac{B_{0}}{R_{0}^{2}} (2 ι + r ι') \frac{\partial \vec{r}}{\partial φ}, \end{matrix}$

(4)

where $\frac{\partial \vec{r}}{\partial r}$ and $\frac{\partial \vec{r}}{\partial φ}$ are covariant basis vectors. The modulus of the total magnetic field is

$\begin{matrix} B_{w} = B_{0} (1 + \frac{A}{R_{0}} (2 ι + r ι') \sin N ξ + \frac{A^{2} M^{2}}{4 r^{2}} \cos 2 N ξ), \end{matrix}$

(5)

where $ξ = \frac{M}{N} θ + φ .$ We determine the new magnetic flux surfaces of the total magnetic field with the islands

$(\vec{B} + {\vec{B}}_{1}) \cdot \nabla Ψ^{*} = 0,$

(6)

Thus, the new magnetic surface equation is given as

$Ψ^{*} = \frac{{ι'}_{0} {(r^{2} - r_{0}^{2})}^{2}}{4} - \frac{{ι'}_{0} w^{2}}{8} \cos (N ξ) .$

(7)

The derivation of equation (7) is given in appendix. Here, $ι_{0}^{'}$ denotes the derivative at $r^{2} = r_{0}^{2},$ and the half-width of the magnetic island is $w = 2 \sqrt{|2 A R_{0} / ι_{0}^{'}|} .$ $\vec{B} \cdot \nabla Ψ^{*} = 0$ denotes that $Ψ^{*}$ is a flux surface quantity. Equations (5) and (7) show that the periodicity of the total magnetic field is mainly generated by the helical angle of the magnetic island. Thus, herein, we only consider the periodicity of the total magnetic field caused by the magnetic island. The coordinate system $(Ψ^{*}, θ, ξ)$ is introduced as follows. The metric for the magnetic island coordinate is

$\begin{matrix} g^{Ψ Ψ} = \nabla Ψ^{*} \cdot \nabla Ψ^{*} = r^{2} {ι'}_{0}^{2} {(r^{2} - r_{0}^{2})}^{2} \\ + M^{2} \frac{A^{2}}{r^{2}} R_{0}^{2} \sin^{2} N ξ + N^{2} A^{2} \sin^{2} N ξ . \end{matrix}$

(8)

Outside the magnetic island, the normalized magnetic flux surface can be written as

$\frac{Ψ^{*} / A R_{0} + 1}{2} = \frac{1}{k^{2}} .$

(9)

From equations (7) and (9), the relation between $r$ and $k$ can be obtained:

$r^{2} - r_{0}^{2} = σ_{\pm} \frac{w}{k} \cos γ .$

(10)

Here, the radial position outside the magnetic island is $0 < k < 1,$ where $k \sin (N ξ / 2) = \sin γ,$ and $- \arcsin (k) \leq γ \leq \arcsin (k) = l .$ When $r^{2} - r_{0}^{2} > 0,$ $σ_{\pm} = 1,$ and when $r^{2} - r_{0}^{2} < 0,$ $σ_{\pm} = - 1 .$

Furthermore, inside the magnetic island, the normalized magnetic flux surface can be written as

$\frac{Ψ^{*} / A R_{0} + 1}{2} = κ^{2},$

(11)

$r^{2} - r_{0}^{2} = w κ \cos β .$

(12)

Here, the radial position inside the magnetic island is $0 < κ < 1,$ where $\sin (N ξ / 2)$ $= κ \sin β .$ Equations (9) and (11) show that the normalized parameter $k$ ( $κ$ ) has a one-to-one correspondence with $Ψ^{*} .$ Thus, the island coordinate systems $(κ, β, ϕ)$ and $(k, γ, ϕ)$ are introduced inside and outside the magnetic island, respectively, where $ϕ$ is the toroidal angle of the original equilibrium magnetic field. Therefore, the Alfvén wave couplings are induced by the periodicity of the magnetic island. The Jacobian $J = \sqrt{g}$ of the island coordinates $(κ, β, ϕ)$ is

$1 / \sqrt{g_{i}} = (\nabla κ \times \nabla β) \cdot \nabla ϕ = \frac{M \cos α}{R_{0} w κ},$

(13)

and outside the island the Jacobian is

$1 / \sqrt{g_{o}} = (\nabla k \times \nabla γ) \cdot \nabla ϕ = - \frac{k^{3}}{w} \frac{M \cos α}{R_{0}} .$

(14)

The rotational transform inside and outside the magnetic island can be obtained based on the definition of rotational transform:

$ι_{i} = \frac{\int_{0}^{2 π} d ϕ \sqrt{g_{i}} B^{β}}{\int_{0}^{2 π} d β \sqrt{g_{i}} B^{ϕ}},$

(15)

$ι_{o} = \frac{\int_{0}^{2 π} d ϕ \sqrt{g_{o}} B^{γ}}{\int_{0}^{2 π} d γ \sqrt{g_{o}} B^{ϕ}} .$

(16)

Here, $ι_{i}$ and $ι_{o}$ are the rotational transforms inside and outside the magnetic island, respectively. $B^{β},$ $B^{γ}$ and $B^{ϕ}$ are contravariant components of magnetic field in $β,$ $γ,$ and $ϕ$ directions, respectively.

Outside the island, i.e. $Ψ^{*} / A R_{0} \geq 1,$ the rotational transform from equation (16) can be described as

$ι_{o} = \frac{π M {ι'}_{0} w}{4 k K (k)},$

(17)

where $K (k)$ is the complete elliptic integral of first kind. Inside the island, i.e. $- 1 \leq Ψ^{*} / A R_{0} \leq 1,$ the rotational transform from equation (15) can be described as

$ι_{i} = \frac{π M {ι'}_{0} w}{4 K (κ)} .$

(18)

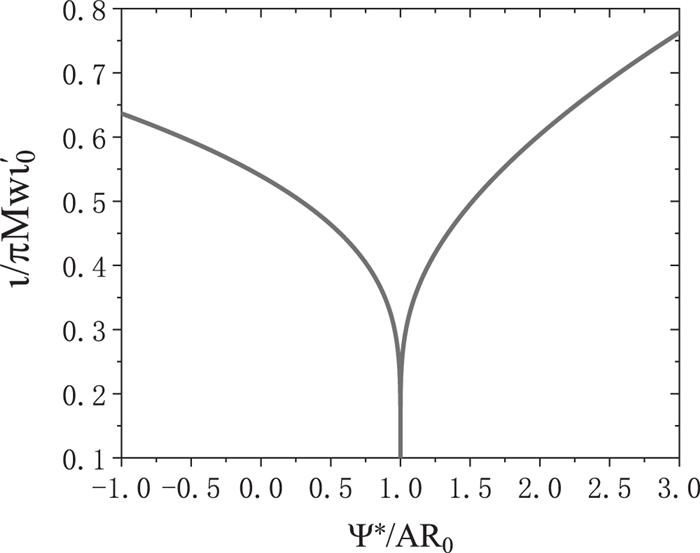
Figure 1 shows the rotational transform inside and outside the island. The results well agree with the past numerical calculations of Cook et al [16]. Here, $ι_{0}^{'} = - 0.3282775$ and island mode number $M = 3 .$

Figure 1. Island rotational transformation inside and outside the island. Outside the island,

$Ψ^{*} / A R_{0} \geq 1,$ and inside the island,

$- 1 \leq Ψ^{*} / A R_{0} \leq 1 .$

DownLoad: Full-Size Img PowerPoint

The new rotation transformation values, $ι_{i}$ and $ι_{o},$ are only dependent on the radial coordinates. We use new coordinates $(κ, β^{*}, ϕ)$ inside the magnetic island and $(k, γ^{*}, ϕ)$ outside the island so that the parallel gradient operators become

$\nabla_{| |} = \frac{ι_{i}}{R_{0}} \frac{\partial}{\partial β^{*}} + \frac{1}{R_{0}} \frac{\partial}{\partial ϕ},$

(19)

$\nabla_{| |} = \frac{ι_{o}}{R_{0}} \frac{\partial}{\partial γ^{*}} + \frac{1}{R_{0}} \frac{\partial}{\partial ϕ} .$

(20)

Thus, we have

$\frac{\vec{B} \cdot \nabla β^{*}}{B} = \frac{ι_{i}}{R_{0}},$

(21)

$\frac{\vec{B} \cdot \nabla γ^{*}}{B} = \frac{ι_{o}}{R_{0}} .$

(22)

Solving equations (21) and (22), we can obtain

$β^{*} (κ, β) = \frac{π M {ι'}_{0} w κ}{2 K (κ)} \int_{0}^{β} \frac{\cos t}{(M ι_{0}^{'} w κ \cos t + N) \sqrt{1 - κ^{2} \sin^{2} t}} d t,$

(23)

$γ^{*} (k, γ) = \frac{π M {ι'}_{0} w}{2 k K (k)} \int_{0}^{γ} \frac{\cos t}{(M {ι'}_{0} w \cos t + N k) \sqrt{1 - \sin^{2} t / k^{2}}} d t .$

(24)

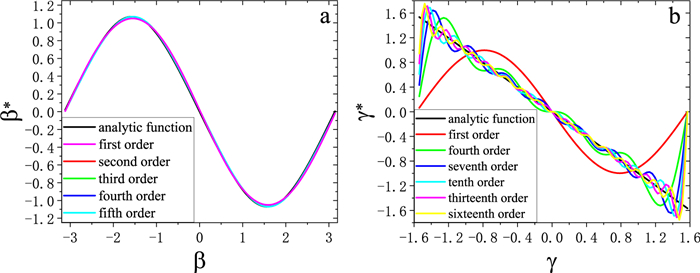
Figures 2(a) and (b) show a visualization of $β^{*}$ and $γ^{*},$ respectively. We find that the contour of $β^{*}$ forms an island inside the magnetic island as shown in figure 2(a) and diverges far away from the island as shown in figure 2(b). The results inside the island are consistent with the island contours in the [16], qualitatively. However, the contour lines concentrate near the island separatrix, where $Ψ^{*} / A R_{0} = 1,$ which implies that the Alfvén waves can accumulate at the separatrix.

Figure 2. Island coordinate system for island mode number

$M_{is} = 3$ and

$N_{is} = - 1,$ (a) inside the island and (b) outside the island, where

$ε = M ι_{0}^{'} w .$

DownLoad: Full-Size Img PowerPoint

In the new coordinates the Jacobians also become

$\begin{matrix} \frac{1}{\sqrt{g_{i}}} = (\nabla κ \times \nabla β^{*}) \cdot \nabla ϕ \\ = \frac{π M^{2} ι_{0}^{'}}{2 R_{0} K (κ)} \frac{\cos β}{(M ι_{0}^{'} w κ \cos β + N)}, \end{matrix}$

(25)

$\begin{matrix} \frac{1}{\sqrt{g_{o}}} = (\nabla k \times \nabla γ^{*}) \cdot \nabla ϕ \\ = - \frac{π M^{2} ι_{0}^{'} k^{2}}{2 R_{0} K (k)} \frac{\cos γ}{M ι_{0}^{'} w \cos γ + N k} . \end{matrix}$

(26)

3. Shear Alfvén wave physics equation with a magnetic island

Starting from the ideal MHD vorticity equation [18–24],

$\begin{matrix} \nabla \cdot [\frac{ω^{2}}{V_{A}^{2}} \nabla_{⊥} Φ] + \vec{B} \cdot \nabla [\frac{1}{B^{2}} \nabla \cdot (B^{2} \nabla_{⊥} (\frac{\vec{b} \cdot \nabla Φ}{B}))] \\ - \nabla (\frac{J_{| |}}{B}) \cdot (\nabla (\frac{\vec{b} \cdot \nabla Φ}{B}) \times \vec{B}) + 2 \frac{\vec{κ} \cdot (\vec{B} \times \nabla δ P)}{B^{2}} = 0, \end{matrix}$

(27)

where $\vec{b} = \vec{B} / B$ is the unit vector of the equilibrium magnetic field, $\vec{κ} = \vec{b} \cdot \nabla \vec{b}$ is the curvature of the equilibrium magnetic field, $J_{| |}$ is the parallel current density, $δ P$ is the perturbed pressure, and $V_{A} = B / \sqrt{μ_{0} ρ}$ is the Alfvén velocity on the magnetic axis. Herein, a low-pressure approximation ( $P / (B^{2} / 2 μ_{0}) ≪ 1$ ) and a small inverse aspect ratio are considered. Finally, we ignore the second-order terms $O (ε^{2})$ and obtain the Alfvén wave physics equation:

$\nabla \cdot (\frac{ω^{2}}{V_{A}^{2}} \nabla_{⊥} Φ) \approx - B \cdot \nabla [\frac{1}{B^{2}} \nabla \cdot (B^{2} \nabla_{⊥} (\frac{b \cdot \nabla Φ}{B}))] .$

(28)

First, we study the Alfvén continuum inside the magnetic island, and the calculation outside the magnetic island can be similarly solved. Herein, the Alfvén continuum is mainly investigated, and we will solve the equation wherein the sum of the coefficients of the second radial derivatives is equal to zero. The operator $\nabla_{⊥} ~ \partial / \partial r^{2} ~ \partial / \partial κ .$ The left- and right-hand sides of equation (28) can be expressed, respectively, as

$ω^{2} \nabla \cdot (\frac{\nabla_{⊥} Φ}{V_{A}^{2}}) \approx ω^{2} \frac{1}{\sqrt{g}} \frac{\partial}{\partial κ} (\sqrt{g} \frac{1}{V_{A}^{2}} g^{κ κ} \frac{\partial}{\partial κ} Φ),$

(29)

$\begin{matrix} - B \cdot \nabla [\frac{1}{B^{2}} \nabla \cdot (B^{2} \nabla_{⊥} (\frac{b \cdot \nabla Φ}{B}))] \\ = - B_{w} \sum_{i, j = 1}^{3} \nabla_{| |} [\frac{1}{B^{2}} \frac{1}{\sqrt{g}} \frac{\partial}{\partial x^{i}} (\sqrt{g} g^{i j} B^{2} \frac{\partial}{\partial x^{j}} (\frac{\nabla_{| |} Φ}{B}))] . \end{matrix}$

(30)

Here, $g^{i j}$ is a metric and $x^{i}$ or $x^{j}$ stands for $κ$ ( $k$ ), $β^{*}$ ( $γ^{*}$ ), and $ϕ .$ Since the continuum structure of Alfvénic waves is determined by setting the determinant of the coefficients of the second-order derivative terms (with respect to the $κ$ ( $k$ )) to zero [22, 25], using equations (28)–(30), the Alfvén continuum equation can be transformed into

$ω^{2} \frac{1}{V_{A}^{2}} g^{κ κ} \tilde{Φ} = - B_{w} \nabla_{| |} [g^{κ κ} (\frac{1}{B} \nabla_{| |} \tilde{Φ})],$

(31)

where $\tilde{Φ} = \partial^{2} Φ / \partial κ^{2}$ inside the island, and

$g^{κ κ} = 2 r_{0}^{2} + 3 w κ \cos β + 2 r_{0}^{2} \cos 2 β + w κ \cos 3 β,$

(32)

outside the island $\tilde{Φ} = \partial^{2} Φ / \partial k^{2},$ and

$\begin{matrix} g^{k k} = 2 r_{0}^{2} + 3 σ_{\pm} \frac{w}{k} \cos γ + 2 r_{0}^{2} \cos 2 γ \\ + σ_{\pm} \frac{w}{k} \cos 3 γ . \end{matrix}$

(33)

$Φ$ is expanded as a Fourier series $\tilde{Φ} = \sum_{n} \sum_{m} {\tilde{Φ}}_{m, n} \exp [i (m π β^{*} / l_{i} + n ϕ)],$ $l_{i} = β^{*} (κ, π / 2)$ is the boundary of $β^{*}$ in equation (23) and ${\tilde{Φ}}_{m, n} = \partial^{2} Φ_{m, n} / \partial κ^{2} .$ Using the parallel operator in equation (19), we can transform equation (31) into

$\begin{matrix} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{i} m π / l_{i} + n)}^{2}] g^{κ κ} \tilde{Φ} \\ = - i (ι_{i} \frac{\partial g^{κ κ}}{\partial β^{*}} + \frac{\partial g^{κ κ}}{\partial ϕ}) (ι_{i} m π / l_{i} + n) \tilde{Φ}, \end{matrix}$

(34)

where $ω_{A}^{2} = V_{A}^{2} / R_{0}^{2} .$ Outside the magnetic island the continuum equation can be similarly obtained and we have

$\begin{matrix} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{o} m π / l_{o} + n)}^{2}] g^{k k} \tilde{Φ} \\ = - i (ι_{o} \frac{\partial g^{k k}}{\partial γ^{*}} + \frac{\partial g^{k k}}{\partial ϕ}) (ι_{o} m π / l_{o} + n) \tilde{Φ}, \end{matrix}$

(35)

where $l_{o} = γ^{*} (k, \arcsin k),$ $\tilde{Φ} = \sum_{n} \sum_{m} {\tilde{Φ}}_{m, n} \exp [i (m π γ^{*} / l_{o} + n ϕ)],$ and ${\tilde{Φ}}_{m, n} = \partial^{2} Φ_{m, n} / \partial k^{2} .$ The equations (34) and (35) show the physics of Alfvén waves, the left-hand side is shear Alfvén wave part and the coupling between different mode numbers arises from $g^{k k}$ (or $g^{κ κ}$ ), and the right-hand side of the equation is the coupling parts arise from the periodicity of helical angle.

The quantities in equations (34) and (35) are

$\begin{matrix} ι_{i} / l_{i} \\ \approx \frac{N}{2} \frac{1}{\arcsin (κ) + q_{0} ι_{0}^{'} w σ_{c} [(1 - κ^{2}) F (κ, \frac{π}{2}) - E (κ, \frac{π}{2})] + {(q_{0} ι_{0}^{'} w)}^{2} [(κ^{2} - \frac{1}{2}) \arcsin (κ) + \frac{1}{2} κ \sqrt{1 - κ^{2}}]}, \end{matrix}$

(36)

$\begin{matrix} ι_{o} / l_{o} \\ \approx \frac{1}{2} \frac{N}{[\frac{π}{2} - q_{0} ι_{0}^{'} w \frac{1}{k} σ_{c} E (k, π / 2) + \frac{π}{2} {(q_{0} ι_{0}^{'} w)}^{2} (\frac{1}{k^{2}} - \frac{1}{2})]}, \end{matrix}$

(37)

where $E (k, π / 2)$ is the complete elliptic integral of the second kind and $q_{0} = M / N .$ If there is no island, the Alfvén continuum should be $ω / ω_{A} = m ι + n,$ where $ι = ι_{0} + ι_{0}^{'} (r^{2} - r_{0}^{2}),$ and the results are shown in figure 3(a). If there is an island, we make an approximation $ι = ι_{0} + ι_{0}^{'} w κ \cos β$ inside the island, and $ι = ι_{0} + ι_{0}^{'} \frac{w}{k} \cos γ$ outside the island, then take an average with respect to $α$ from $(- π, π)$ and obtain

$\begin{matrix} ω / ω_{A} = m ι + n \approx m ι_{0} + n \\ - \frac{2}{π} m ι_{0}^{'} w σ_{c} [(1 - κ^{2}) F (κ, \frac{π}{2}) - E (κ, \frac{π}{2})], \end{matrix}$

(38)

$\begin{matrix} ω / ω_{A} = m ι + n \approx m ι_{0} + n \\ + \frac{2}{π} m ι_{0}^{'} w σ_{c} \frac{1}{k} E (k, π / 2) . \end{matrix}$

(39)

Figure 3. Alfvén continuum in a cylinder without an island (a), and with an island (b), where

$ι_{0} = 1 / 3,$

$ι_{0}^{'} = - 0.3282775$ and the rational surface is at

$r_{0}^{2} / a^{2} = 0.4547124 .$ Inside the island the lines of color are different from those outside the island.

DownLoad: Full-Size Img PowerPoint

The results are shown in figure 3(b). Equation (38) is valid in the region of $(r^{2} - r_{0}^{2}) \in [- w, w]$ and equation (39) is available in the region of $|r^{2} - r_{0}^{2}| > w .$ We find that the continuum at the rational surface $ι_{0} = 1 / 3$ is also equal to 0 when an island exists. However, the island changes the frequency of continuum at the separatrix. The continuum frequency is shifted as $~ m ι_{0}^{'} w .$

If neglecting the coupling terms on the right-hand side of equation (35), we can use the relation $ω / ω_{A} = (ι_{o} m π / l_{o} + n)$ in the region of $|r^{2} - r_{0}^{2}| > w$ and the formula is approximated as

$\begin{matrix} ω / ω_{A} = ι_{o} m π / l_{o} + n \\ \approx M m ι_{0} + n + \frac{2}{π} m M ι_{0}^{'} w σ_{c} \frac{1}{k} E (k, π / 2) . \end{matrix}$

(40)

Comparing equations (39) and (40), we find that the formulae are a bit different, and the results of equation (40) are shown in figure 4(a). Inside the island the continua are not equal to zero at the island O point as shown in figure 4(b). The minimum continuum is at $ω / ω_{A} = M m ι_{0} + n + 2 m M ι_{0}^{'} w / π$ according to equation (40), when $k = 1,$ or $κ = 1$ at the separatrix. The frequency shift is $Δ ω / ω_{A} = M Δ m ι_{0} + 2 Δ m M ι_{0}^{'} w / π$ under the same toroidal mode number $n .$ We note that at the bottom of the continuum the lines open at $(r^{2} - r_{0}^{2}) \in [- w, w] .$ Neglecting the coupling terms on the right-hand side of equation (34), we use equation (36) and can obtain the continuum inside the magnetic island. But $l_{i}$ is too small inside the island when the continuum goes to the island O point and $κ = 0,$ according to equation (36) the continuum $ω / ω_{A} = (ι_{i} m π / l_{i} + n)$ will go to infinity. However, it is not the case and we adopt an interpolation method to remove the singularity, and the results are shown in figure 4(b). Comparing figures 4(a) and (b), the continuum goes to minimum at the island separatrix and then increases inside the magnetic island, which is consistent with Biancalani's work [14].

Figure 4. Island continuum outside the magnetic island (a) and inside the island (b). The continuum lines of (a) are given by equation (40) and lines of (b) are derived from equations (34) and (36). An interpolation method is used to remove the singularity near the

$r^{2} = r_{0}^{2} .$

DownLoad: Full-Size Img PowerPoint

In the following part, we try to solve the eigenvalues inside and outside the island. Let us begin from the equation (34), the continuum equation inside the magnetic island. We multiply both sides of equation (34) with $1 / \sqrt{g_{i}}$ and $\exp [- i (m' π β^{*} / l_{i} + n' ϕ)],$ take an integral with respect to $ϕ$ from $- π$ to $π,$ and obtain

$\begin{matrix} \sum_{m} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{i} m π / l_{i} + n')}^{2}] \frac{1}{\sqrt{g_{i}}} g^{κ κ} \\ {\tilde{Φ}}_{m, n'} \exp [i (m - m') π β^{*} / l_{i}] \\ = - i \sum_{m} \frac{1}{\sqrt{g_{i}}} (ι_{i} \frac{\partial β}{\partial β^{*}} + \frac{\partial β}{\partial ϕ}) \frac{\partial g^{κ κ}}{\partial β} (ι_{i} m π / l_{i} + n') \\ {\tilde{Φ}}_{m, n'} \exp [i (m - m') π β^{*} / l_{i}] . \end{matrix}$

(41)

Using equations (18), (23), (25) and the relation $\sin (N ξ / 2) = κ \sin β,$ we can transform equation (41) into

$\begin{matrix} \sum_{m} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{i} m π / l_{i} + n')}^{2}] \frac{g^{κ κ} \cos β}{(M ι_{0}^{'} w κ \cos β + N)} \\ {\tilde{Φ}}_{m, n'} \exp [i (m - m') π β^{*} / l_{i}] \\ = - i \sum_{m} \frac{1}{2 κ} (\sqrt{1 - κ^{2} \sin^{2} β} + \frac{N \sqrt{1 - κ^{2} \sin^{2} β}}{(M ι_{0}^{'} w κ \cos β + N)}) \\ \times \frac{\partial g^{κ κ}}{\partial β} (ι_{i} m π / l_{i} + n') {\tilde{Φ}}_{m, n'} \exp [i (m - m') π β^{*} / l_{i}], \end{matrix}$

(42)

The term in the left-hand side of equation (42) is an even function with respect to $β$ and can be expressed in Fourier cosine series. The part in the right-hand side can be expressed in Fourier sine series. We have

$\frac{a_{0}}{2} + \sum_{j = 1}^{\infty} a_{j} \cos (j π β^{*} / l_{i}) = \frac{g^{κ κ} \cos β}{(M ι_{0}^{'} w κ \cos β + N)}$

(43)

$\begin{matrix} \sum_{j = 1}^{\infty} b_{j} \sin (j π β^{*} / l_{i}) = (1 + \frac{N}{(M ι_{0}^{'} w κ \cos β + N)}) \\ \times \sqrt{1 - κ^{2} \sin^{2} β} \frac{\partial g^{κ κ}}{\partial β} \end{matrix}$

(44)

$a_{j} = \frac{1}{l_{i}} \int_{- l_{i}}^{l_{i}} d β^{*} g^{κ κ} \frac{\cos β \cos (j π β^{*} / l_{i})}{(M ι_{0}^{'} w κ \cos β + N)}$

(45)

$\begin{matrix} b_{j} = \frac{1}{l_{i}} \int_{- l_{i}}^{l_{i}} d β^{*} (1 + \frac{N}{(M ι_{0}^{'} w κ \cos β + N)}) \\ \times \sqrt{1 - κ^{2} \sin^{2} β} \frac{\partial g^{κ κ}}{\partial β} \sin (j π β^{*} / l_{i}) \end{matrix}$

(46)

$\sin (j π β^{*} / l_{i}) = \frac{\exp (i j π β^{*} / l_{i}) - \exp (- i j π β^{*} / l_{i})}{2 i}$

(47)

$\cos (j π β^{*} / l_{i}) = \frac{\exp (i j π β^{*} / l_{i}) + \exp (- i j π β^{*} / l_{i})}{2}$

(48)

Substituting equations (43)–(46) into equation (42), we get

$\begin{matrix} \sum_{m} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{i} m π / l_{i} + n')}^{2}] [a_{0} \exp [i (m - m') π β^{*} / l_{i}] \\ + \sum_{j = 1}^{\infty} a_{j} [\exp (i (m + j - m') π β^{*} / l_{i}) \\ + \exp (i (m - j - m') π β^{*} / l_{i})]] {\tilde{Φ}}_{m, n'} \\ = - \sum_{m} \frac{1}{2 κ} \sum_{j = 1}^{\infty} b_{j} [\exp (i (m + j - m') π β^{*} / l_{i}) \\ - \exp (i (m - j - m') π β^{*} / l_{i})] (ι_{i} m π / l_{i} + n') {\tilde{Φ}}_{m, n'} . \end{matrix}$

(49)

We integrate $β^{*}$ from $- l_{i}$ to $l_{i},$ and obtain

$\begin{matrix} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{i} m π / l_{i} + n')}^{2}] [a_{0} δ_{m, m'} \\ + \sum_{j = 1}^{\infty} a_{j} (δ_{m + j, m'} + δ_{m - j, m'})] {\tilde{Φ}}_{m, n'} \\ = - \frac{1}{2 κ} \sum_{j = 1}^{\infty} b_{j} [δ_{m + j, m'} - δ_{m - j, m'}] (ι_{i} {m π / l}_{i} + n') {\tilde{Φ}}_{m, n'}, \end{matrix}$

(50)

where $δ_{m; m'}$ is the Kronecker symbol. When $m = m',$ $δ_{m; m'} = 1 .$ Equation (50) represents the shear Alfvén wave equation inside the magnetic island.

Next, the continua outside the magnetic island are calculated. The coordinates $(k, γ^{*}, ϕ)$ are adopted, where $- γ^{*} (k, \arcsin k) \leq γ^{*} \leq γ^{*} (k, \arcsin k) = l_{o},$ and $γ^{*} (k, \arcsin k)$ is given by equation (24). It is similar to the method inside magnetic island. We multiply both sides of equation (35) with $1 / \sqrt{g_{o}}$ and $\exp [- i (m' π γ^{*} / l_{o} + n' ϕ)],$ take an integral with respect to $ϕ$ from $- π$ to $π,$ and we obtain the shear Alfvén continuum equation outside the magnetic island

$\begin{matrix} \sum_{m} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{o} m π / l_{o} + n')}^{2}] \frac{g^{k k} \cos γ}{M ι_{0}^{'} w \cos γ + N k} \\ \times {\tilde{Φ}}_{m, n'} \exp [i (m - m') π γ^{*} / l_{o}] \\ = - i \frac{1}{2} (1 + \frac{N k}{M ι_{0}^{'} w \cos γ + N k}) {(1 - \sin^{2} γ / k^{2})}^{1 / 2} \\ \times \frac{\partial g^{k k}}{\partial γ} \sum_{m} (ι_{o} m π / l_{o} + n') {\tilde{Φ}}_{m, n'} \exp [i (m - m') π γ^{*} / l_{o}] . \end{matrix}$

(51)

The even part in the left-hand side of equation can be expressed in Fourier cosine series and the odd component in the right-hand side can be expansion in Fourier sine series. We obtain

$\frac{c_{0}}{2} + \sum_{j = 1}^{\infty} c_{j} \cos (j π γ^{*} / l_{o}) = \frac{g^{k k} \cos γ}{M ι_{0}^{'} w \cos γ + N k},$

(52)

$\begin{matrix} \sum_{j = 1}^{\infty} d_{j} \sin (j π γ^{*} / l_{o}) = ({(1 - \sin^{2} γ / k^{2})}^{1 / 2} \\ + \frac{N k {(1 - \sin^{2} γ / k^{2})}^{1 / 2}}{M ι_{0}^{'} w \cos γ + N k}) \frac{\partial g^{k k}}{\partial γ}, \end{matrix}$

(53)

$c_{j} = \frac{1}{l_{o}} \int_{- l_{o}}^{l_{o}} d γ^{*} \frac{g^{k k} \cos γ}{M ι_{0}^{'} w \cos γ + N k} \cos (j π γ^{*} / l_{o}),$

(54)

$\begin{matrix} d_{j} = \frac{1}{l_{o}} \int_{- l_{o}}^{l_{o}} d γ^{*} (1 + \frac{N k}{M ι_{0}^{'} w \cos γ + N k}) \\ \times {(1 - \sin^{2} γ / k^{2})}^{1 / 2} \frac{\partial g^{k k}}{\partial γ} \sin (j π γ^{*} / l_{o}) . \end{matrix}$

(55)

Then, similar to the treatment inside the magnetic island both sides of equation (51) are integrated with respect to $γ^{*}$ within $(- l_{o}, l_{o}) .$ The shear Alfvén wave continuum equation outside the magnetic island is

$\begin{matrix} [\frac{ω^{2}}{ω_{A}^{2}} - {(ι_{o} m π / l_{o} + n')}^{2}] [c_{0} δ_{m, m'} \\ + \sum_{j = 1}^{\infty} c_{j} (δ_{m + j, m'} + δ_{m - j, m'})] {\tilde{Φ}}_{m, n'} \\ = - \frac{1}{2} \sum_{j = 1}^{\infty} d_{j} [δ_{m + j, m'} - δ_{m - j, m'}] (ι_{o} m π / l_{o} + n') {\tilde{Φ}}_{m, n'} . \end{matrix}$

(56)

Noting that in equations (45), (46), (54) and (55) the integral is complicate, we take the equations (45) and (54) as an example.

$a_{j} = \frac{1}{l_{i}} \int_{- l_{i}}^{l_{i}} d β \frac{d β^{*}}{d β} g^{κ κ} \frac{\cos β \cos (j π β^{*} / l_{i})}{(M ι_{0}^{'} w κ \cos β + N)}$

(57)

$c_{j} = \frac{1}{l_{o}} \int_{- l_{o}}^{l_{o}} d γ \frac{d γ^{*}}{d γ} \frac{g^{k k} \cos γ}{M ι_{0}^{'} w \cos γ + N k} \cos (j π γ^{*} / l_{o}) .$

(58)

Using equations (23) and (24), we can transform the integral with respect to $β^{*}$ and $γ^{*}$ into an integral with respect to $β$ and $γ,$ respectively. However, there are $\cos (j π β^{*} / l_{i})$ and $\cos (j π γ^{*} / l_{o})$ in the integrals, thus we make a Fourier series expansion of the integrals in the equations (23) and (24) and obtain

$\begin{matrix} \sum_{j = 1}^{\infty} e_{j} \sin (j β) \\ = \int_{0}^{β} d t \frac{\cos t}{(M ι_{0}^{'} w κ \cos t + N) \sqrt{1 - κ^{2} \sin^{2} t}}, \end{matrix}$

(59)

$\begin{matrix} \sum_{j = 1}^{\infty} f_{j} \sin (j π γ / l) \\ = \int_{0}^{γ} d t \frac{\cos t}{(M ι_{0}^{'} w \cos t + N k) \sqrt{1 - \sin^{2} t / k^{2}}}, \end{matrix}$

(60)

where $l = \arcsin k$ and $j$ is the order number. We plot the fitting functions of different orders, and the results are shown in figure 5. We find that $β^{*}$ can be fitted by the first order expansion and the fitting functions of $γ^{*}$ are hard to converge near the boundary, even very high order.

Figure 5. The periodicity of the coupling coordinates when

$κ = 1$ inside the magnetic island and

$k = 1$ outside the magnetic island. (a) The relationship between

$β$ and

$β^{*}$ and (b) the dependence of

$γ^{*}$ on

$γ .$ The analytic functions of

$β^{*}$ and

$γ^{*}$ are given by equations (23) and (24), respectively. The other lines of (a) and (b) are produced by the equations (59) and (60), respectively.

DownLoad: Full-Size Img PowerPoint

As a result, the quantity inside the island can be expressed as

$j π β^{*} / l_{i} \approx j Z \sin β,$

(61)

$Z = \frac{N π κ e_{1}}{T},$

(62)

$T = \int_{0}^{π / 2} \frac{\cos t}{(M ι_{0}^{'} w κ \cos t + N) \sqrt{1 - κ^{2} \sin^{2} t}} d t .$

(63)

A new quantum number $p$ emerges in equation (50)

$\begin{matrix} \exp [i j π β^{*} / l_{i}] = \exp [i j Z \sin β] \\ = \sum_{p = - \infty}^{+ \infty} J_{p} (j Z) \exp (i p β) . \end{matrix}$

(64)

In the papers of Cook and Biancalani, they also found new quantum numbers and discrete coupling inside the magnetic island [14, 16]. Our analytic calculations are consistent with the previous work. The new quantum number makes the coupling more complicate, and we will discuss it in a future paper.

4. Numerical results

Equations (50) and (56) represent the shear Alfvén wave continuum equations inside and outside the magnetic island, respectively, which can solve the eigenvalues. Next, we convert the equations to matrices as follows:

$(\vec{B} - λ \vec{A}) \vec{X} = 0,$

(65)

where the eigenvalue is $λ = ω^{2} / ω_{A}^{2},$ i.e. the normalized Alfvén wave frequency, and $\vec{X} = {(Φ "_{1, n'}, Φ "_{2, n'}, \dots, Φ "_{m, n'})}^{T}$ is the eigenfunction. For the equation (50)

$\vec{A} = a_{0} δ_{m, m'} + \sum_{j = 1}^{\infty} a_{j} (δ_{m + j, m'} + δ_{m - j, m'}),$

(66)

$\begin{matrix} \vec{B} = {(ι_{i} m π / l_{i} + n')}^{2} [a_{0} δ_{m, m'} + \sum_{j = 1}^{\infty} a_{j} (δ_{m + j, m'} + δ_{m - j, m'})] \\ - \frac{1}{2 κ} \sum_{j = 1}^{\infty} b_{j} [δ_{m + j, m'} - δ_{m - j, m'}] (ι_{i} m π / l_{i} + n') . \end{matrix}$

(67)

Thus, the solving of the eigenvalues of equation (65) is transformed into the calculation of the eigenvalues of the matrix ${\vec{A}}^{- 1} \vec{B},$ where ${\vec{A}}^{- 1}$ is the inverse matrix of $\vec{A} .$ The matrix ${\vec{A}}^{- 1} \vec{B}$ is transformed into a Heisenberg matrix via the elementary similarity transformation, and then, the double-step QR (orthogonal trigonometric decomposition) method with the origin shifts is employed to solve all the eigenvalues of the Heisenberg matrix. Thereafter, the continuous spectrum of different radial positions can be obtained. The W7-X parameters are chosen. The major radius $R_{0} = 5.499992 m,$ minor radius $a = 0.5502758 m,$ and the perturbation amplitude $A = - 6.1271521 0^{- 6}$ m. Moreover, the position of the rational surface is $r_{0} = 0.370877 m .$ Figures 6(a) and (b) show the continua of different mode numbers. In figure 6 the low m mode Alfvén waves are hard to couple with island configuration and there is no gap. The continua inside and outside the magnetic island converge to the island separatrix, and the minimum frequency also appears at the island separatrix. The island makes the continuum frequency shift up. In [13, 14] and [16], it is also found that there is no coupling for the low mode number. Our results are consistent with theirs.

Figure 6. The low m mode Alfvén continua. (a) Two branches of Alfvén wave and (b) Alfvén waves of three sets of low mode numbers.

DownLoad: Full-Size Img PowerPoint

With increasing poloidal mode number, the coupling phenomenon can be seen inside and outside the magnetic island. Figure 7 shows the coupling between Alfvén waves of more than three branches. The coupling induces a frequency gap between continua with $Δ m \geq 2,$ the m = 2 low mode number continuum is upshifted to high frequency, and the m = 4 mode continuum with high frequency is changed into the m = 2 mode with low frequency. Between the gaps, there is also m = 3 continuum, as shown in figure 7(a). In figure 7(b) we also observe the gaps with continuum frequency changing and the mode number changes $Δ m \geq 4 .$ Between the gaps there are also several continua with different mode numbers. In some experiments, the obvious frequency change of Alfvén mode occurs when the magnetic island exists [26, 27]. Our theoretic results prove the large continuum frequency change with low mode number and can be used to explain the experimental observation, qualitatively. As shown in figure 7(a), when $Δ m = 2,$ the continuum couplings and the frequency exchange phenomenon can be observed. The $Δ m = 2$ and $Δ m = 4$ couplings arise from the ellipticity produced by the island, which is consistent with the mechanism in Biancalani et al [13–15]. However, the ellipticity only exchanges a section of the continua, which is different from Biancalani's work, wherein the continua with very high poloidal mode numbers yield gaps [13–15].

Figure 7. Shear Alfvén continuum in the presence of a magnetic island with multiple-mode couplings. The mode number of the magnetic island

$M_{is} = 3,$ and

$N_{is} = - 1 .$ (a) Four-mode coupling, (b) five-mode coupling.

DownLoad: Full-Size Img PowerPoint

In the following part, we continue to increase the poloidal mode number to the continuum spectrum both inside and outside the magnetic island. Figure 8 displays the results. In figure 8(a) the continua are similar with those in figure 8(b). It implies that the couplings mainly arise from the periodicity of $β^{*}$ and $γ^{*} .$ Two obvious frequency shifts occur between the $m = 3$ and the $m = 10$ continua. Near the island separatrix the coupling phenomenon of the continua occurs more frequently. The coupling is a bit complicate and the adjacent continua couple with each other. A section of the high frequency continuum with high poloidal mode number changes into low frequency and in contrast the corresponding section of low frequency continuum with low mode number upshifts to high frequency. In the TJ-II stellarator [12], Sun et al determined that the frequency of the Alfvén wave abruptly changes, but the mode number of the Alfvén wave does not change when it couples with the magnetic island. This is consistent with our numerical results.

Figure 8. Shear Alfvén continua with multiple-mode couplings in the presence of a magnetic island. The mode numbers of the magnetic island are

$M_{is} = 3,$

$N_{is} = - 1 .$ (a)

$n = 1$ and (b)

$n = 0 .$

DownLoad: Full-Size Img PowerPoint

5. Conclusions and discussion

A shear Alfvén continuum spectrum in the presence of a magnetic island with a cylinder configuration was obtained by solving MHD equations. Only the periodicity provided by the magnetic island for exciting the shear Alfvén wave mode was considered. Moreover, we confirmed that the magnetic island can induce coupling. In continua with high poloidal mode numbers and multiple-mode number couplings, continuum gaps may be present. At the island separatrix, the magnetic island induces an upshift in frequencies of the continuum. These results agree with the previous numerical simulation results of Biancalani et al [13–15] and Cook et al [16, 17]. However, we found that the upshift of frequency $Δ ω^{2}$ is proportional to the square of the poloidal mode number $~ m^{2},$ and the coupling phenomenon of the continuum inside and outside the magnetic island becomes more significant and complex with increasing poloidal mode number. For the coupling phenomenon found herein, a frequency change was present in the continuum. The phenomenon was compared with the experimental results of the TJ-II stellarator [12], which may explain the experimental observations for the TJ-II stellarator. We will analyze it in a future paper.

Herein, the Alfvén wave continuum structure inside and outside the magnetic island was studied. Unlike Biancalani et al [13–15] who regard magnetic islands as a tokamak, we analyzed not only the ellipticity-induced coupling but also the multiple-mode coupling. The magnetic-island-induced Alfvén wave continua in stellarators are quite different from those in tokamaks. Moreover, the magnetic perturbation is considerably smaller than those in tokamaks. We did not study the toroidal couplings, and the three-dimensional effects produced by magnetic islands will be investigated in a future paper. Magnetic geometry with multiple periodicities contributed by the toroidal field, magnetic island, and triangularity is more common in a real device. Thus, multiple-mode couplings are very important and complex for not only stellarators but also tokamaks when a magnetic island is introduced to the magnetic configuration. Therefore, understanding the structure of a shear Alfvén continuum in the presence of magnetic islands is an important step for analyzing complex eigenmodes.

Appendix A. Island flux surface $Ψ^{*}$

When there is a magnetic island, it needs to construct an auxiliary magnetic surface $Ψ^{*},$ which satisfies

${\vec{B}}_{w} \cdot \nabla Ψ^{*} = 0,$

(A1)

where ${\vec{B}}_{w} = \vec{B} + {\vec{B}}_{1},$ $\vec{B}$ is the equilibrium magnetic field, and ${\vec{B}}_{1}$ is produced by the magnetic island. The parallel operators have the following forms

$\vec{B} \cdot \nabla = \frac{B_{0}}{R_{0}} (ι \frac{\partial}{\partial θ} + \frac{\partial}{\partial φ}),$

(A2)

$\begin{matrix} {\vec{B}}_{1} \cdot \nabla = \frac{B_{0}}{r} (\frac{\partial \tilde{ψ}}{\partial θ} - \frac{r^{2}}{R_{0}^{2}} ι \frac{\partial \tilde{ψ}}{\partial φ}) \frac{\partial}{\partial r} \\ + \tilde{ψ} \frac{B_{0}}{R_{0}^{2}} (2 ι + r ι') \frac{\partial}{\partial φ}, \end{matrix}$

(A3)

where $\tilde{ψ}$ is the perturbation contributed by the island. From equation (A1) it has

$\vec{B} \cdot \nabla Ψ^{*} = - {\vec{B}}_{1} \cdot \nabla Ψ^{*} .$

(A4)

In equation (A3) we take $\tilde{ψ} = A \exp [i (M θ + N φ)],$ then equation (A4) can be written as

$\begin{matrix} \frac{1}{ε} i \tilde{ψ} (M - ε^{2} N ι) \frac{\partial Ψ^{*}}{\partial r} + ι \frac{\partial Ψ^{*}}{\partial θ} \\ + (\tilde{ψ} \frac{1}{R_{0}} (2 ι + r ι') + 1) \frac{\partial Ψ^{*}}{\partial φ} = 0 . \end{matrix}$

(A5)

Here, $Ψ^{*}$ is expanded as a Fourier series as

$Ψ^{*} = \sum_{k, j} ψ_{k, j} \exp [i (k θ + j φ)] .$

(A6)

The equation (A5) can be transformed into

$\begin{matrix} \sum_{k, j} [\frac{1}{ε} (M - ε^{2} N ι) \frac{\partial ψ_{k, j}}{\partial r} + j \frac{1}{R_{0}} (2 ι + r ι') ψ_{k, j}] A \\ \times \exp [i ((k + M) θ + (j + N) φ)] \\ + \sum_{k, j} (k ι + j) ψ_{k, j} \exp [i (k θ + j φ)]) = 0 . \end{matrix}$

(A7)

Both sides of equation (A3) are multiplied with $\exp [- i (k' θ + j' φ)],$ integrating in one period, then we obtain

$\begin{matrix} \sum_{k, j} [\frac{1}{ε} (M - ε^{2} N ι) \frac{\partial ψ_{k, j}}{\partial r} + j \frac{1}{R_{0}} (2 ι + r ι') ψ_{k, j}] \\ \times A δ_{k + M, k'; j + N, j'} + \sum_{k, j} (k ι + j) ψ_{k, j} δ_{k, k'; j, j'} = 0 . \end{matrix}$

(A8)

When $k' = M,$ and $j' = N,$ we get

$(M - ε^{2} N ι) A \frac{\partial ψ_{0, 0}}{\partial r} + \frac{r}{R_{0}} (M ι + N) ψ_{M, N} = 0 .$

(A9)

Using $ι_{0} = - N / M,$ we can obtain

$ψ_{M, N} = - \frac{R_{0} (1 + ε^{2} ι ι_{0})}{r (ι - ι_{0})} A \frac{\partial ψ_{0, 0}}{\partial r} .$

(A10)

If equation (A10) is not singular, we assume that

$\frac{\partial ψ_{0, 0}}{\partial r} = r \sum_{j \geq 1} C_{j} {(ι - ι_{0})}^{j} .$

(A11)

Since $ψ_{M, N}$ is a constant and independent of $r,$ we let $j = 1,$ and $C_{1} = 1,$ and then we get

$ψ_{M, N} = - R_{0} A (1 + ε^{2} ι ι_{0}) \approx - A R_{0},$

(A12)

where $ε^{2} ≪ 1 .$ We use the approximation

$ι \approx ι_{0} + {\frac{\partial ι}{\partial r^{2}}|}_{r^{2} = r_{0}^{2}} (r^{2} - r_{0}^{2}),$

(A13)

then the $ψ_{0, 0}$ can be obtained

$\begin{matrix} ψ_{0, 0} = {\frac{\partial ι}{\partial r^{2}}|}_{r^{2} = r_{0}^{2}} \int r (r^{2} - r_{0}^{2}) d r \\ = \frac{1}{4} {\frac{\partial ι}{\partial r^{2}}|}_{r^{2} = r_{0}^{2}} {(r^{2} - r_{0}^{2})}^{2} . \end{matrix}$

(A14)

Finally, $Ψ^{*}$ can be expressed as

$\begin{matrix} Ψ^{*} = \frac{1}{4} {\frac{\partial ι}{\partial r^{2}}|}_{r^{2} = r_{0}^{2}} {(r^{2} - r_{0}^{2})}^{2} \\ - A R_{0} \exp [i (M θ + N φ)] . \end{matrix}$

(A15)

We take the real part of equation (A15) and obtain

$Ψ^{*} = \frac{ι_{0}^{'} {(r^{2} - r_{0}^{2})}^{2}}{4} - A R_{0} \cos (N ξ),$

(A16)

where $ι_{0}^{'} = {\frac{\partial ι}{\partial r^{2}}|}_{r^{2} = r_{0}^{2}},$ and $A R_{0} = ι_{0}^{'} w^{2} / 8 .$

Acknowledgments

The corresponding author, Dr Cao, appreciates the helpful discussions with Dr Axel Könies in Max-Planck-Institute for Plasma Physics in Greifswald. This work is supported by the ITER Project of Ministry of Science and Technology (No. 2022YFE03080002), National Natural Science Foundation of China (Nos. 11605088 and 12005100), the Key Scientific Research Program of Education Department of Hunan Province (Nos. 20A417 and 20A439), the National Magnetic Confinement Fusion Science Program of China (No. 2015GB110002), the Hunan Provincial Natural Science Foundation of China (No. 2017JJ3268), the International Cooperation Base Project of Hunan Province of China (No. 2018WK4009), the Key Laboratory of Magnetic Confinement Nuclear Fusion Research in Hengyang (No. 2018KJ108), and the PhD Start-Up Fund of University of South China (No. 2017XQD08).

References (27)

References

[1]	Chen L and Zonca F 2016 Rev. Mod. Phys. 88 015008 doi: 10.1103/RevModPhys.88.015008
[2]	Wong K L 1999 Plasma Phys. Control. Fusion 41 R1 doi: 10.1088/0741-3335/41/1/001
[3]	Wong K L et al 1991 Phys. Rev. Lett. 66 1874 doi: 10.1103/PhysRevLett.66.1874
[4]	Cheng C Z, Chen L and Chance M S 1985 Ann. Phys. 161 21 doi: 10.1016/0003-4916(85)90335-5
[5]	Turnbull A D et al 1993 Phys. Fluids B 5 2546 doi: 10.1063/1.860742
[6]	Heidbrink W W et al 1993 Phys. Rev. Lett. 71 855 doi: 10.1103/PhysRevLett.71.855
[7]	Heidbrink W W et al 1999 Phys. Plasmas 6 1147 doi: 10.1063/1.873359
[8]	Xu M et al 2013 Plasma Phys. Control. Fusion 55 065002 doi: 10.1088/0741-3335/55/6/065002
[9]	Buratti P et al 2005 Nucl. Fusion 45 1446 doi: 10.1088/0029-5515/45/11/027
[10]	Annibaldi S V, Zonca F and Buratti P 2007 Plasma Phys. Control. Fusion 49 475 doi: 10.1088/0741-3335/49/4/010
[11]	Zimmermann O et al 2005 Coupling of Alfvén-like modes and large 2/1 tearing modes at TEXTOR Proc. of the 32nd EPS Conf. on Plasma Physics Tarragona (Tarragona) (EPS)
[12]	Sun B J, Ochando M A and López-Bruna D 2015 Nucl. Fusion 55 093023 doi: 10.1088/0029-5515/55/9/093023
[13]	Biancalani A et al 2010 Phys. Rev. Lett. 105 095002 doi: 10.1103/PhysRevLett.105.095002
[14]	Biancalani A et al 2011 Plasma Phys. Control. Fusion 53 025009 doi: 10.1088/0741-3335/53/2/025009
[15]	Biancalani A et al 2010 Phys. Plasmas 17 122106 doi: 10.1063/1.3531689
[16]	Cook C R and Hegna C C 2015 Phys. Plasmas 22 042517 doi: 10.1063/1.4919266
[17]	Cook C R et al 2016 Plasma Phys. Control. Fusion 58 054004 doi: 10.1088/0741-3335/58/5/054004
[18]	Breizman B N et al 2003 Phys. Plasmas 10 3649 doi: 10.1063/1.1597495
[19]	Breizman B N et al 2005 Phys. Plasmas 12 112506 doi: 10.1063/1.2130692
[20]	Yu L M et al 2013 Phys. Plasmas 20 082509 doi: 10.1063/1.4817962
[21]	Fu G Y and Berk H L 2006 Phys. Plasmas 13 052502 doi: 10.1063/1.2196246
[22]	Xie H S and Xiao Y 2015 Phys. Plasmas 22 022518 doi: 10.1063/1.4913487
[23]	Cheng C Z and Chance M S 1986 Phys. Fluids 29 3695 doi: 10.1063/1.865801
[24]	Spong D A, Azevedo E D and Todo Y 2010 Phys. Plasmas 17 022106 doi: 10.1063/1.3313818
[25]	Fu G Y and Van Dam J W 1989 Phys. Fluids B 1 1949 doi: 10.1063/1.859057
[26]	Chen W et al 2014 Europhys. Lett. 107 25001 doi: 10.1209/0295-5075/107/25001
[27]	Chen W et al 2017 Nucl. Fusion 57 114003 doi: 10.1088/1741-4326/aa7eee

[1]	Wenjin Chen, Min Zhang, Zhiwei Ma. Interaction of dynamic magnetic island with bootstrap current in toroidal plasma[J]. Plasma Science and Technology. DOI: 10.1088/2058-6272/adac91
[2]	Junhui YANG, Jinjia CAO, Jianhua ZHAO, Yongzhi DAI, Dong XIANG. Alfvén continuum in the presence of a magnetic island in a cylinder configuration[J]. Plasma Science and Technology, 2023, 25(3): 035102. DOI: 10.1088/2058-6272/ac9de0
[3]	Sunggeun LEE, Hankwon LIM. Landau damping of twisted waves in Cairns distribution with anisotropic temperature[J]. Plasma Science and Technology, 2021, 23(8): 85001-085001. DOI: 10.1088/2058-6272/ac01be
[4]	Bowen RUAN (阮博文), Zhoujun YANG (杨州军), Xiaoming PAN (潘晓明), Hao ZHOU (周豪), Fengqi CHANG (常风岐), Jing ZHOU (周静). Estimation of magnetic island width by the fluctuations of electron cyclotron emission radiometer on J-TEXT[J]. Plasma Science and Technology, 2019, 21(1): 15102-015102. DOI: 10.1088/2058-6272/aae382
[5]	LIANG Shaoyong (梁绍勇), XIAO Bingjia (肖炳甲), ZHANG Yang (张洋), WANG Linfang (王淋芳), YUAN Qiping (袁旗平), LUO Zhengping (罗正平), SHI Tonghui (石同辉), TI Ang (提昂). Real-Time Detection for Magnetic Island of Neoclassical Tearing Mode in EAST Plasma Control System[J]. Plasma Science and Technology, 2016, 18(2): 197-201. DOI: 10.1088/1009-0630/18/2/17
[6]	JIANG Peng (江澎), LIN Zhihong (林志宏), Ihor HOLOD, XIAO Chijie (肖池阶). The Implementation of Magnetic Islands in Gyrokinetic Toroidal Code[J]. Plasma Science and Technology, 2016, 18(2): 126-130. DOI: 10.1088/1009-0630/18/2/05
[7]	T. S. HAHM. Ion Heating from Nonlinear Landau Damping of High Mode Number Toroidal Alfvén Eigenmodes[J]. Plasma Science and Technology, 2015, 17(7): 534-538. DOI: 10.1088/1009-0630/17/7/02
[8]	QU Hongpeng (曲洪鹏). Ion-Banana-Orbit-Width Effect on Bootstrap Current for Small Magnetic Islands[J]. Plasma Science and Technology, 2013, 15(9): 852-856. DOI: 10.1088/1009-0630/15/9/03
[9]	HAN Xiang (韩翔), LING Bili (凌必利), GAO Xiang (高翔), LIU Yong (刘永), TI Ang (提昂), LI Erzhong (李二众), XU Liqing (徐立清), WANG Yumin (王嵎民). Measurement of Magnetic Island Width by Multi-Channel ECE Radiometer on HT-7 Tokamak[J]. Plasma Science and Technology, 2013, 15(3): 217-220. DOI: 10.1088/1009-0630/15/3/05
[10]	XU Hui (徐慧), SHENG Zhengming (盛政明). Critical Initial Amplitude of Langmuir Wave Damping[J]. Plasma Science and Technology, 2012, 14(3): 181-268. DOI: 10.1088/1009-0630/14/3/01