| Citation: | Debing ZHANG, Pengfei ZHAO, Yingfeng XU, Lei YE, Xianmei ZHANG. Gyrokinetic simulations of the kinetic electron effects on the electrostatic instabilities on the ITER baseline scenario[J]. Plasma Science and Technology, 2024, 26(9): 095101. DOI: 10.1088/2058-6272/ad4e78 |
The linear and nonlinear simulations are carried out using the gyrokinetic code NLT for the electrostatic instabilities in the core region of a deuterium plasma based on the International Thermonuclear Experimental Reactor (ITER) baseline scenario. The kinetic electron effects on the linear frequency and nonlinear transport are studied by adopting the adiabatic electron model and the fully drift-kinetic electron model in the NLT code, respectively. The linear simulations focus on the dependence of linear frequency on the plasma parameters, such as the ion and electron temperature gradients κTi,e≡R/LTi,e, the density gradient κn≡R/Ln and the ion–electron temperature ratio τ=Te/Ti. Here, R is the major radius, and Te and Ti denote the electron and ion temperatures, respectively. LA=−(∂rlnA)−1 is the gradient scale length, with A denoting the density, the ion and electron temperatures, respectively. In the kinetic electron model, the ion temperature gradient (ITG) instability and the trapped electron mode (TEM) dominate in the small and large kθ region, respectively, where kθ is the poloidal wavenumber. The TEM-dominant region becomes wider by increasing (decreasing) κTe (κTi) or by decreasing κn. For the nominal parameters of the ITER baseline scenario, the maximum growth rate of dominant ITG instability in the kinetic electron model is about three times larger than that in the adiabatic electron model. The normalized linear frequency depends on the value of τ, rather than the value of Te or Ti, in both the adiabatic and kinetic electron models. The nonlinear simulation results show that the ion heat diffusivity in the kinetic electron model is quite a lot larger than that in the adiabatic electron model, the radial structure is finer and the time oscillation is more rapid. In addition, the magnitude of the fluctuated potential at the saturated stage peaks in the ITG-dominated region, and contributions from the TEM (dominating in the higher kθ region) to the nonlinear transport can be neglected. In the adiabatic electron model, the zonal radial electric field is found to be mainly driven by the turbulent energy flux, and the contribution of turbulent poloidal Reynolds stress is quite small due to the toroidal shielding effect. However, in the kinetic electron model, the turbulent energy flux is not strong enough to drive the zonal radial electric field in the nonlinear saturated stage. The kinetic electron effects on the mechanism of the turbulence-driven zonal radial electric field should be further investigated.
The programmatic objective of the ITER project [1] is to demonstrate the scientific and technological feasibility of fusion energy for peaceful purposes. The operational approaches developed in the ITER Research Plan [1] include the pre-fusion power operation (PFPO) and the fusion power operation (FPO). A key milestone for the PFPO will be the demonstration of L-mode plasmas at the full technical capability of the device with full current (15 MA) and full field (5.3 T). The FPO mainly focuses on the H-mode in deuterium/deuterium–tritium plasmas, which is expected to achieve the long-pulse (300–500 s) Q⩾ goal at power levels of \sim500 MW, and to make significant progress towards the achievement of Q\sim5 for burn durations of \sim3000 s in non-inductive plasmas.
Comprehensive integrated modeling is a powerful tool to predict the plasma properties for various operations with specified discharge conditions, such as the magnetic equilibrium configuration, the plasma profiles, the electrostatic and electromagnetic instabilities, and the turbulent transport and confinement property [2–9]. The early simulations carried out in ITER hybrid and target steady-state fusion burn scenarios using the PTRANSP integrated modeling code indicated that the fusion power production reached approximately 500 MW in the hybrid scenario, and ranged from 168 MW up to 226 MW in the target steady-state scenario [2]. By using the transport simulation code CORSICA, the accessible ITER hybrid scenario condition and achievable range of plasma parameters were systematically investigated. Useful techniques for avoiding the poloidal field coil current were found, and the enhancement of the plasma energy confinement and fusion power generation with various heating schemes was foreseen for ITER advanced operations [3]. The assessment of density evolution in the ITER baseline scenario using the integrated model JINTRAC indicated that stable but cyclical operational regimes could be achieved for a pellet-fuelled ITER ELMy H-mode scenario with Q=10 [5]. Later, JINTRAC was used to model the most efficient fuelling schemes for the non-active and nuclear phases of ITER plasma scenarios, as well as core-SOL/divertor simulations of helium plasmas and of the full deuterium–tritium Q=10 scenario, including the current ramp-up/down diverted phases [9]. It is concluded that JINTRAC may be helpful for the establishment of suitable control schemes for particle and power exhaust in burning ITER deuterium–tritium plasma scenarios.
Analogous to the integrated modeling, numerical simulations using gyrokinetic codes are a widely used approach for the prediction of the micro-instabilities and turbulent transport in ITER scenarios [10–14]. Gyrokinetic simulations of ion temperature gradient (ITG)-driven turbulence in real-size systems such as ITER were carried out using the ORB5 code. It was pointed out that several numerical schemes, such as noise control and field-aligned Fourier filtering procedures, are essential in obtaining numerically healthy results. The nonlinear simulation results showed that the zonal flow behavior is quite different between the circular cross-section and the ITER-shaped equilibrium plasma, and the heat transport was found to be dramatically reduced when going from circular to ITER-shaped plasmas [11]. A multi-scale nature of instabilities in the ITER PFPO plasma scenario was presented by means of global electromagnetic gyrokinetic simulations with the ORB5 code, and it was reported that the unstable micro-instabilities in the scale of the ion gyro-radius are located in the region with a toroidal wavenumber of about 150–220 [14].
In this work, the electrostatic instabilities, including the ITG instability and trapped electron mode (TEM), are studied in the ITER baseline scenario using the NLT code [15–17]. Specifically, the kinetic electron effects on the linear instabilities and nonlinear turbulent transport are systematically studied by adopting the adiabatic and kinetic electron models in NLT, respectively. The remaining part of this paper is organized as follows. In section 2, the theory fundamentals of the NLT code and the simulation setup based on the ITER baseline scenario are introduced; in section 3, the parameter dependences for the ITG instability and TEM in the linear version are given; in section 4, the nonlinear characteristics driven by the electrostatic instabilities are studied; section 5 provides a conclusion.
In this section, we first give a brief introduction of the NLT code, and then illustrate the setup of simulation parameters used in NLT based on the ITER baseline scenario.
In terms of the gyrocenter coordinates \boldsymbol{Z}=(\boldsymbol{X},\ v_{\parallel},\ \mu,\ \xi) , the nonlinear gyrokinetic Vlasov equation used in the NLT code is
| \frac{ {\rm{d}} F_j}{ {\rm{d}} t}=\frac{\partial F_j}{\partial t}+\dot{{\boldsymbol{X}}}\cdot\nabla F_j+\dot{v}_\parallel\frac{\partial F_j}{\partial v_\parallel}=0. | (1) |
Here, {\boldsymbol{X}} is the gyrocenter position, v_\parallel is the parallel velocity, \mu is the magnetic moment, and \xi is the gyro-angle. F_j(\boldsymbol{X},\ v_{\parallel},\ \mu,\ t) is the gyrocenter distribution function of j -species, with j= i and e denoting the ions and electrons, respectively.
In the electrostatic situation, the perturbed electrostatic potential \delta\phi is obtained by solving the quasi-neutrality equation, which is given by
| \sum\limits_{j={\rm{i,e}}}e_j(\delta n_j^{\rm{g}}+\delta n_j^{\rm{p}})=0. | (2) |
Here,
| \tag{3a} \delta n_j^{\rm{g}}=2{\text{π}} \int\delta\bar F_j\frac{B_\parallel^*}{m_j} {\rm{d}}\mu {\rm{d}} v_\parallel , | (3) |
denotes the perturbed gyrocenter density. \delta F_j=F_j-F_{0j} , with \delta F _j and F_{0j} denoting the perturbed and equilibrium parts of the distribution function, respectively. B_\parallel^*={\boldsymbol{b}}\cdot{\boldsymbol{B}}^* is the Jacobian of the phase-space coordinates {{\boldsymbol{Z}}} , {\boldsymbol{B}}^*={\boldsymbol{B}}+\dfrac{m_j}{e_j} v_\parallel\nabla\times{\boldsymbol{b}} , where {\boldsymbol{B}} is the background magnetic field with the direction denoted as {\boldsymbol{b}} , and m_j and e_j are the mass and charge of j -species, respectively. (\overline{\cdots}) denotes the gyroaverage, which is defined as
| \bar A({\boldsymbol{X}},\mu, v_\parallel,t)=\frac1{2\pi}\oint A({\boldsymbol{X}}+\boldsymbol\rho,\mu, v_\parallel,t) {\rm{d}}\xi, |
with \boldsymbol\rho(\mu,\xi) the Larmor radius.
| \tag{3b} \delta n_j^{\rm{p}}=\int {\rm{d}}^6{{\boldsymbol{Z}}}\delta({\boldsymbol{X}}+\boldsymbol\rho_j-{\boldsymbol{x}})\frac{e_j}{B}\frac{\partial F_j}{\partial\mu}[\delta\phi({\boldsymbol{X}}+\boldsymbol\rho_j)-\overline{\delta\phi}({\boldsymbol{X}},\mu)] , | (3b) |
denotes the perturbed polarization density. {\rm{d}}^6{{\boldsymbol{Z}}}= B_\parallel^* {\rm{d}}^3{\boldsymbol{X}} {\rm{d}} v_\parallel {\rm{d}}\mu {\rm{d}}\xi , and {\boldsymbol{x}} is the particle position. Note that in the NLT code, the gyroaverage operator in equation (3b) for the polarization density is rigorously calculated, instead of using the long wavelength limit, where \delta n_j^{\rm{p}}\approx\nabla\cdot(\dfrac{e_jn_{0j}}{T_j}\rho_j^2\nabla_\perp)\delta\phi with T_j and n_{0j} the equilibrium temperature and density, respectively, thus all of the k_\perp\rho terms are retained in the quasi-neutrality equation (2) [17], with k_\perp the perpendicular wavenumber. In the adiabatic electron model, the perturbed density for electrons is assumed as
| \delta n_{\rm{e}}=e_{\rm{e}}n_{{\rm{0e}}}\frac{\delta\phi-\langle\delta\phi\rangle} {T_{\rm{e}}}, | (4) |
with \langle\cdots\rangle denoting the magnetic-flux-surface average.
In the NLT code, the I-transform perturbation method [18–20], a special Lie-transform perturbation method, has been used to solve the nonlinear gyrokinetic Vlasov equation (1). The I-transform method is used to separate the perturbation part of the gyrocenter motion from the unperturbed gyrocenter motion. In the I-transform method, the relationship between the gyrocenter phase-space coordinates {{\boldsymbol{Z}}} and the new coordinates {{\boldsymbol{Z}}}^{*} up to {\cal{O}}(\epsilon_{\rm{\delta}}^2) is
| \tag{5a} Z^{*a}=Z^a+G_1^a+G_2^a+\frac12G_1^k\partial_kG_1^a. | (5a) |
Here, \epsilon_{\rm{\delta}}=\delta F/F_0\ll1 , and {\boldsymbol{G}}_1 and {\boldsymbol{G}}_2 are the first-order and second-order generating vector fields, respectively. The superscript a and the symbol k denote the a -component and k -component of phase-space coordinates {{\boldsymbol{Z}}} , respectively. According to the scalar invariance F({{\boldsymbol{Z}}})=F^{*}({{\boldsymbol{Z}}}^{*}) , with F^{*} the distribution function in terms of {{\boldsymbol{Z}}}^{*} , the transformation for the distribution function is
| \tag{5b} F=F^{*}+(G_1^a+G_2^a)\partial_aF^{*}+\frac12G_1^k\partial_k(G_1^a\partial_aF^{*}). | (5b) |
For the I-transform, the new coordinate {{\boldsymbol{Z}}}^* is chosen so that the Vlasov equation in terms of {{\boldsymbol{Z}}}^* is formally identical to the unperturbed one; that is,
| \frac{ {\rm{d}}_0}{ {\rm{d}} t}F^*=0. | (6) |
Here, the total time derivative ( {\rm{d}}/ {\rm{d}} t)_0 is taken along the unperturbed orbit. The contributions due to the perturbed fields are reflected by the n th-order generating vector fields, which are calculated as
| G_n^a=\partial_kS _nJ^{ka}, | (7) |
where n=1,2 . J^{ka} is the component of the Poisson matrix in the unperturbed guiding-center coordinates, and S _n is the n th-order scalar gauge function, which satisfies
| \tag{8a}\frac{ {\rm{d}}_0}{ {\rm{d}} t}S _1=e_{\rm{i}}\overline{\delta\phi}, | (8a) |
| \tag{8b} \frac{ {\rm{d}}_0}{ {\rm{d}} t}S _2=-\frac12e_{\rm{i}}\partial_mS _1J^{mn}\partial_n\overline{\delta\phi}, | (8b) |
in the electrostatic situation. In the realistic numerical computation, the S_ 2 term is neglected, which is proved to be the ordering of {\cal{O}}(\epsilon_\delta^2\epsilon_t^3) during a short time interval \Delta t [21], where \epsilon_t=\omega\Delta t .
In the NLT code, the semi-Lagrangian approach was used to solve the gyrokinetic equations (6) and (8a). Since the perturbed part of the gyrocenter motion is decoupled from the unperturbed part due to the I-transform, a 4D tensor spline interpolation in the fixed points [22] is used for the improvement of numerical efficiency. The earliest version of the NLT code is developed with the adiabatic electron in the electrostatic limit. The magnetic flux coordinates (\psi,\theta,\zeta) are adopted, with \psi the poloidal magnetic flux, \theta the poloidal angle and \zeta the toroidal angle. It is verified by the linear geodesic acoustic mode test and the standard cyclone base case (CBC) for the linear ITG test [15]. Then, it is upgraded in the field-aligned coordinates (\psi,\alpha,\theta) with \alpha=q\theta-\zeta , where q is the safety factor. The Fourier filter based on the pseudo-spectral method is also used. Nonlinear tests of the NLT code for numerically studying the ITG-driven turbulence with the CBC parameters are carried out [16]. Both the linear and nonlinear results by NLT agree well with those using other gyrokinetic codes, such as GENE and ORB5. Later, NLT is extended to include the magnetic axis in the simulation domain, in which the artificial boundary near the magnetic axis is replaced by the natural boundary [23]. Furthermore, the fully drift-kinetic effects of electrons are included in NLT. By taking this new approach, NLT is successfully used to simulate the TEM-driven turbulence [17]. In addition, the interface module of NLT has been developed, and can be used to read the experimental magnetic equilibrium and plasma profiles. For example, NLT has been successfully used in the analysis of the electrostatic turbulence for a typical experiment in EAST [24]. In this work, we use the NLT code to study the ion gyroradius-scale electrostatic instabilities and the associated turbulence in the ITER baseline scenario; the electron gyroradius-scale instabilities, such as the electron temperature gradient instability, are left as a future work.
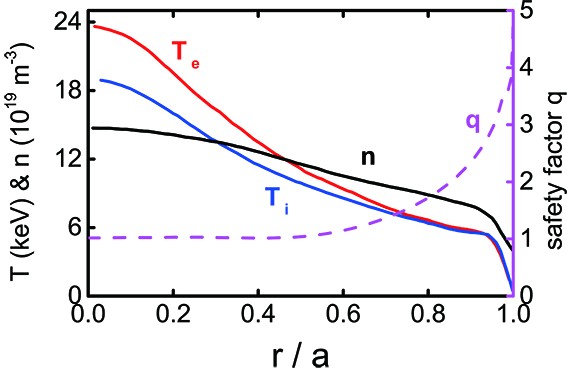
The magnetic configuration and plasma profiles on the ITER baseline scenario are shown in figures 1 and 2, respectively. The major radius is R_0=6.2 m, the minor radius is a=2.0 m, and the magnetic field at the axis is B_0=5.3 T. The plasma profiles are adapted from reference [25], in which the temperature and density profiles originate from the simulations using the integrated modeling TGYRO combined with TGLF-SAT1 for the ITER 50–50 deuterium–tritium fully inductive reference scenario at 5.3 T/15 MA, with 33 MW NBI and 20 MW ECRH heating. In this work, only the case with a deuterium plasma is considered.
Because of the Fourier filter scheme used in NLT, a convergence test of frequency on the spatial grids is necessary. In figure 3, the real frequency and growth rate for k_\theta\rho_{\rm{s}}=0.5 with the adiabatic electron model in terms of different radial and poloidal grid meshes (N_\psi, N_\theta) are shown. Here, k_\theta is the poloidal wavenumber, \rho_{\rm{s}}=c_{\rm{s}}/\Omega_{\rm{i}} with c_{\rm{s}}=\sqrt{T_{\rm{i}}/m_{\rm{i}}} and \Omega_{\rm{i}}=e_{\rm{i}}B/m_{\rm{i}} . Note that the definition of c_{\rm{s}} in this work relates to the local ion temperature T_{\rm{i}} , which is not consistent with the definition for ion acoustic velocity by the electron temperature T_{\rm{e}} . The grid numbers in the velocity space are (N_{v_\parallel},N_\mu)=(64,16) , and the grid numbers in the spatial space are varied with N_\psi=(64,128,256,360,512) and N_\theta=(16,32,48) . The simulation domain centered at the diagnosed position r=0.5a is adopted as 20\rho_{\rm{s}} . For computing efficiency, we take \kappa_{T_{\rm{i}}}\equiv R/L_{T_{\rm{i}}}=10.47 for illustration, which is about twice the nominal value. L_{T_{\rm{i}}}=-(\partial_r\ln T_{\rm{i}})^{-1} is the ion temperature scale length. The temperature profile is varied using equation (10), defined in section 3. It is clearly seen that when N_\theta increases from 16 to 32, both the real frequency and growth rate show obvious variations; however, when N_\theta changes from 32 to 48, both the real frequency and growth rate change slightly. On the other hand, for a fixed N_\theta , as N_\psi varies from 64 to 256, the real frequency and growth rate significantly change; however, when N_\psi varies from 256 to 512, both the real frequency and growth rate change slightly. The discrepancies are within 3\% . Clearly, the real frequency and growth rate reach their convergency values with (N_\psi,N_\theta)=(256,32) . Although only the results with k_\theta\rho_{\rm{s}}=0.5 are shown in figure 3, we mention that the scanning for the range of 0.2\leqslant k_\theta\rho_{\rm{s}}\leqslant 0.8 shows similar tendencies. On this basis, in the following linear simulations, we set (N_\psi,N_\theta)=(256,32) .
The linear dispersion relation in the electrostatic situation with the local kinetic limit is governed by the quasi-neutrality condition \int{\rm{d}}^3{{\boldsymbol{v}}}\delta f_{\rm{i}}= \int{\rm{d}}^3{{\boldsymbol{v}}}\delta f_{\rm{e}} . Here, \int{\rm{d}}^3{{\boldsymbol{v}}} is the velocity integral, and the perturbed distribution functions for ions and electrons are [26–29]
| \tag{9a} \delta f_{\rm{i}}=-\frac{e_{\rm{i}}\delta\phi}{T_{\rm{i}}}F_{\rm{0i}}\Bigg\{1-J_0^2\frac{ \hat{\omega}+ k_\theta\rho_{\rm{s}}\big[ \kappa_n+ \kappa_{T_{\rm{i}}}\big(\hat{v}_{\parallel,{\rm{i}}}^2 +\hat{v}_{\perp,{\rm{i}}}^2-1.5\big)\big]}{ \hat{\omega}+ k_\theta\rho_{\rm{s}}(2\hat{v}_{\parallel,{\rm{i}}}^2+\hat{v}_{\perp,{\rm{i}}}^2)}\Bigg\}, | (9a) |
| \tag{9b}\delta f_{\rm{e}}=\frac{e\delta\phi}{T_{\rm{e}}}F_{\rm{0e}}\Bigg\{\big(1-f_{\rm{t}}\big)+f_{\rm{t}}\frac{ \hat{\omega}- k_\theta\rho_{\rm{s}}\tau\big[ \kappa_n+ \kappa_{T_{\rm{e}}}\big(\hat{v}_{\parallel,{\rm{e}}}^2+\hat{v}_{\perp,{\rm{e}}}^2-1.5\big)\big]}{ \hat{\omega}-\alpha\cdot k_\theta\rho_{\rm{s}}\tau(2\hat{v}_{\parallel,{\rm{e}}}^2+\hat{v}_{\perp,{\rm{e}}}^2)}\Bigg\}. | (9b) |
Here, \hat{\omega} is the linear frequency normalized by c_{\rm{s}}/R_0 . \kappa_n\equiv R/L_n and \kappa_{T_{\rm{e}}}\equiv R/L_{T_{\rm{e}}} are the density and electron temperature scale lengths, respectively. L_A\equiv-(\partial_r\ln A)^{-1} . \tau=T_{\rm{e}}/T_{\rm{i}} is the electron–ion temperature ratio. \hat{v}_{\parallel,j} and \hat{v}_{\perp,j} are the parallel and perpendicular velocities normalized by v_{{\rm{th}},j}=\sqrt{2T_j/m_j} , respectively. Both of the ion and electron distribution functions are separated as the adiabatic response (AR) term and the non-adiabatic response (NAR) term. The driving sources due to the spatial inhomogeneity are reflected by \kappa_n and \kappa_{T_{\rm{i}}} in the ion NAR term and by \kappa_n and \kappa_{T_{\rm{e}}} in the electron NAR term. There are also some significant differences in the ion and electron distribution functions. The finite Larmor radius (FLR) effect denoted by J_0^2 is kept in the ion NAR term but neglected in the electron NAR term. The electron NAR term is proportional to the fraction of trapped electrons f_{\rm{t}} . In the adiabatic electron model, f_{\rm{t}}=0 . In addition, the ion NAR term includes the ion magnetic drift resonance, while the electron NAR term includes the electron bounce resonance, in which the bounce-average operation can be approximately reduced by the factor \alpha\approx1.2 [26].
In this section, the parametric dependence on the linear frequency of the electrostatic instability is investigated. The parameters include \kappa_{T_{\rm{i}}} , \kappa_{T_{\rm{e}}} , \kappa_n , \eta_{\rm{i}}= \kappa_{T_{\rm{i}}}/ \kappa_n and \tau=T_{\rm{e}}/T_{\rm{i}} . The profiles are modified by
| A'(r)=\frac{A^k(r)}{A^{k-1}(r_0)} \exp\Big\{-\Big(\frac{r-r_0}{\Delta r}\Big)^2\Big\}. | (10) |
Here, A and A' denote the original and modified plasma profiles, respectively. k is a constant. Obviously, the modified values at r=r_0 are the same as those in the original profiles, but the logarithmic gradient is k times the original ones; that is, A'|_{r_0}=A|_{r_0} while \kappa_{A'}|_{r_0}=k\cdot\kappa_A|_{r_0} . In the following linear simulations, the diagnosed position is taken as r_0=0.5a , at which the nominal values of the parameters are \kappa_{T_{\rm{i0}}}=5.09 , \kappa_{T_{\rm{e0}}}=6.23 , \kappa_{n0}=2.61 and \tau_0\equiv T_{\rm{e}}/T_{\rm{i}}=1.2 . We set \Delta r=0.8a , and k is varied in the range of (0.6,2.0) . When the effects of a certain parameter are studied, the other parameters are kept unchanged unless otherwise stated.
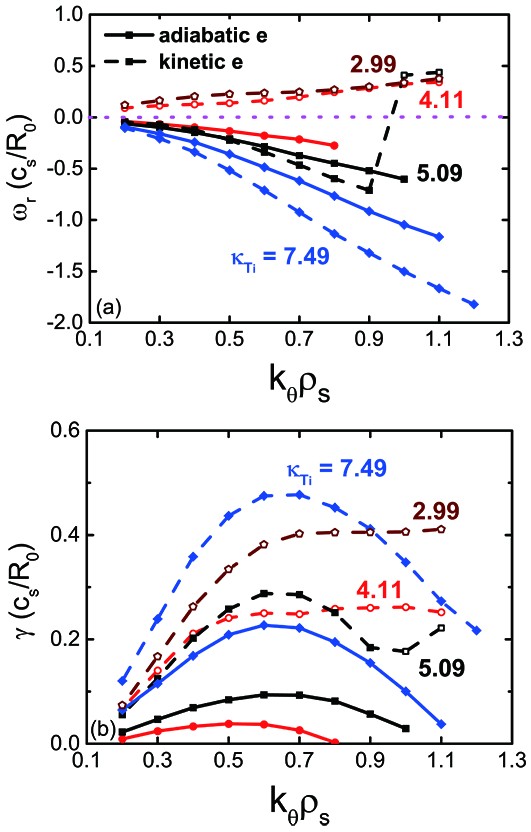
Figure 4 shows the real frequency and growth rate versus k_\theta\rho_{\rm{s}} , with \kappa_{T_{\rm{i}}}=2.99 , 4.11 , 5.09 and 7.49 , which correspond to about 0.6\kappa_{T_{\rm{i0}}} , 0.8\kappa_{T_{\rm{i0}}} , 1.0\kappa_{T_{\rm{i0}}} and 1.5\kappa_{T_{\rm{i0}}} , respectively. The solid and dashed lines represent the results from the adiabatic and kinetic electron models, respectively. The negative (solid symbols) and positive (open symbols) real frequencies denote that the modes propagate in the ion and electron diamagnetic drift directions, respectively, which are known as the ITG instability and TEM.
In the adiabatic electron model, the electrostatic instability is stabilized in the situation with \kappa_{T_{\rm{i}}}=2.99 . For \kappa_{T_{\rm{i}}}\geqslant4.11 , only the ITG instability can be excited. The negative real frequency increases with k_\theta\rho_{\rm{s}} increased for a fixed \kappa_{T_{\rm{i}}} , and increases as \kappa_{T_{\rm{i}}} increases for a fixed k_\theta\rho_{\rm{s}} . The theoretic derivation [26] shows that the normalized real frequency satisfies \hat{\omega}_{\rm{r}}\propto\Gamma_0-\eta_{\rm{i}}b_{\rm{i}}(\Gamma_0-\Gamma_1) , where \Gamma_n= I_n(b_{\rm{i}}){\rm{e}}^{-b_{\rm{i}}} , with I_n the n th modified Bessel function and b_{\rm{i}}=( k_\theta\rho_{\rm{s}})^2 . Clearly, for a fixed b_{\rm{i}} , it is qualitatively seen that the real frequency shifts towards the negative direction with the increase of \eta_{\rm{i}} . Meanwhile, the growth rate shown in figure 4(b) increases firstly and then decreases by enlarging k_\theta\rho_{\rm{s}} for each \kappa_{T_{\rm{i}}} . As \kappa_{T_{\rm{i}}} increases, the growth rate increases significantly, and the maximum growth rate with \kappa_{T_{\rm{i}}}=7.49 is about three times that with \kappa_{T_{\rm{i}}}=4.11 . For the case with a nominal value of \kappa_{T_{\rm{i}}}=5.09 , the maximum growth rate is about 0.094c_{\rm{s}}/R_0 , which appears at around k_\theta\rho_{\rm{s}}=0.7 . In addition, the unstable spectrum becomes wider with larger \kappa_{T_{\rm{i}}} . As shown, the largest k_\theta\rho_{\rm{s}} for the unstable ITG instability increases from about 0.8 to about 1.2 as \kappa_{T_{\rm{i}}} increases from 4.11 to 7.49.
In the kinetic electron model, both the ITG instability and TEM can be excited, and the dominant instability depends on the value of \kappa_{T_{\rm{i}}} . For \kappa_{T_{\rm{i}}}=7.49 , the ITG instability dominates. The real frequency is more negative than that in the adiabatic electron model. On the other hand, although the dependence of the growth rate on k_\theta\rho_{\rm{s}} shows a similar tendency to that in the adiabatic electron model, the value is significantly larger, and the maximum growth rate increases by a factor of about 2.5. This well-known feature was apparently recognized in previous work [30], which revealed that in the situation where ITG instability dominates, the response of the trapped electron is nearly zero. The magnitude of the electron AR term becomes smaller when the trapped electron is included, and then the dielectric constant in the Poisson equation becomes smaller, leading to a larger ITG growth rate. As \kappa_{T_{\rm{i}}} decreases, the real frequency shifts upwards in the electron diamagnetic drift direction. For the nominal value of \kappa_{T_{\rm{i}}}=5.09 , the ITG instability dominates when k_\theta\rho_{\rm{s}}\leqslant0.9 . In the range of k_\theta\rho_{\rm{s}}>0.9 , the ITG-driving source in the ion NAR term becomes smaller due to the FLR effects, and the dominant instability becomes TEM, which is similar to the result in [30]. The maximum growth rate is about 0.288c_{\rm{s}}/R_0 , which is larger than that in the adiabatic electron by a factor of about 3.0. For \kappa_{T_{\rm{i}}}=4.11 , unlike the ITG instability that dominates in the adiabatic electron model, TEM dominates in the range of k_\theta\rho_{\rm{s}}\leqslant1.2 . With the increment of k_\theta\rho_{\rm{s}} , the real frequency increases monotonically; however, the growth rate increases monotonically to its maximum value at about k_\theta\rho_{\rm{s}}=0.5 , and remains almost constant when k_\theta\rho_{\rm{s}}>0.5 . When \kappa_{T_{\rm{i}}} further decreases to 2.99, TEM can be excited in the whole range of k_\theta\rho_{\rm{s}}\leqslant1.2 . The real frequency and growth rate for \kappa_{T_{\rm{i}}}=2.99 are similar to those for \kappa_{T_{\rm{i}}}=4.11 , except that the growth rate is a constant when k_\theta\rho_{\rm{s}}>0.7 . From the viewpoint of electron bounce resonance between the trapped electron and TEM, which is simply written as \hat{\omega}_{\rm{r}}= k_\theta\rho_{\rm{s}} G(v_{\rm{res}}) , with G(v_{\rm{res}}) denoting the resonant velocity factor shown in equation (9b), it is seen that G(v_{\rm{res}}) is almost unchanged when k_\theta\rho_{\rm{s}}>0.5\; (0.7) for \kappa_{T_{\rm{i}}}=4.11\; (2.99) ; namely, the Landau damping effect is nearly the same, leading to a constant growth rate. In this phenomenological explanation, the ion contribution to the growth rate is considered as relatively small in the high- k_\theta\rho_{\rm{s}} region because of the FLR effect. In addition, for a fixed k_\theta\rho_{\rm{s}} , it is seen that the growth rate for \kappa_{T_{\rm{i}}}=4.11 is smaller than that for \kappa_{T_{\rm{i}}}=2.99 . Clearly, the ion NAR term becomes larger for a larger \kappa_{T_{\rm{i}}} , and this term is beneficial for driving ITG instability. On the contrary, the increment of \kappa_{T_{\rm{i}}} shows a stabilizing effect on the TEM.
Figure 5 presents the real frequency and growth rate versus k_\theta\rho_{\rm{s}} with \kappa_{T_{\rm{e}}}=3.06 , 4.34 , 6.23 , 7.03 and 9.00 , which correspond to about 0.5\kappa_{T_{\rm{e0}}} , 0.7\kappa_{T_{\rm{e0}}} , 1.0\kappa_{T_{\rm{e0}}} , 1.2\kappa_{T_{\rm{e0}}} and 1.5\kappa_{T_{\rm{e0}}} , respectively. Obviously, the real frequency and growth rate are independent of \kappa_{T_{\rm{e}}} in the adiabatic electron model; note that it is the electron temperature instead of the electron temperature gradient that appeares in the adiabatic model. However, the situations in the kinetic electron model are quite different. In figure 5(a), it is shown that the ITG instability dominates for \kappa_{T_{\rm{e}}}=3.06 and the TEM dominates for \kappa_{T_{\rm{e}}}=9.00 in the range of 0.2\leqslant k_\theta\rho_{\rm{s}}\leqslant1.2 . The real frequencies for both the dominant ITG instability and dominant TEM increase as k_\theta\rho_{\rm{s}} increases, and the increment for ITG instability is larger than that for TEM. A sharp transition from the dominant ITG instability to the dominant TEM in the higher k_\theta\rho_{\rm{s}} region appears when \kappa_{T_{\rm{e}}}=4.34 , 6.23 and 7.03 ; the smaller \kappa_{T_{\rm{e}}} corresponds to the larger transition value of ( k_\theta\rho_{\rm{s}})_{\rm{TR}} . Clearly, the TEM driving source is weaker when \kappa_{T_{\rm{e}}} is smaller, and the ITG driving source in the ion NAR term should be adequately suppressed by the FLR effects with higher k_\theta\rho_{\rm{s}} ; in this way, the excitation of TEM would be possible with smaller \kappa_{T_{\rm{e}}} . For a fixed k_\theta\rho_{\rm{s}} , the real frequency shifts upwards to the electron diamagnetic drift direction with the increment of \kappa_{T_{\rm{e}}} , which also infers that the transform from ITG instability to TEM can more easily take place with higher \kappa_{T_{\rm{e}}} . It is interesting to find that a continuous TEM-dominant to ITG-dominant transition occurs with \kappa_{T_{\rm{e}}}=7.03 in the range of k_\theta\rho_{\rm{s}}<0.5 . A zeroth real frequency appears at around k_\theta\rho_{\rm{s}}=0.4 . As is discussed in [31], the zeroth real frequency results from the cancellation between the magnetic drift term of trapped electrons and the FLR term of ions. We mention that the continuous transition in the spectra of ITG and TEM is also reported in the studies using a numerical code such as HD7 [28]. This transition has a different character to the ubiquitous mode since the growth rate for the ubiquitous mode is almost the largest at the transition point [32]; however, the growth rate at the transition point shown in figure 5(b) is quite small.
In figure 5(b), the growth rate in the kinetic electron model is significantly larger than that in the adiabatic electron model by a factor of at least 3.0. In the ITG-dominant region, the growth rates are nearly the same for different \kappa_{T_{\rm{e}}} . This is not surprising, since the growth rate for ITG instability mainly depends on the ion magnetic drift resonance, and the fraction of trapped electrons, \kappa_{T_{\rm{e}}} , has little effect on these two factors. In the TEM-dominant region, the growth rate increases monotonically by enlarging \kappa_{T_{\rm{e}}} , indicating that \kappa_{T_{\rm{e}}} shows a destabilizing effect on TEM. For \kappa_{T_{\rm{e}}}=9.00 , the growth rate increases monotonically with the enlargement of k_\theta\rho_{\rm{s}} . The dependence of the growth rate on k_\theta\rho_{\rm{s}} in the k_\theta\rho_{\rm{s}}<0.7 region shows a similar tendency to that of \kappa_{T_{\rm{i}}}=2.99 in figure 4(b). However, the growth rate with k_\theta\rho_{\rm{s}}>0.7 shows an notably faster increment than that with 0.5< k_\theta\rho_{\rm{s}}<0.7 . This behavior is expected from the fact that the ion NAR term contribution with higher k_\theta\rho_{\rm{s}} can be adequately neglected in the large \kappa_{T_{\rm{e}}} regime [29]. From the viewpoint of electron bounce resonance, it is found that in the higher k_\theta\rho_{\rm{s}} region, the resonant velocity factor G(v_{\rm{res}}) increases with k_\theta\rho_{\rm{s}} increased, and then the fraction of resonant particles decreases and the Landau damping effect becomes weaker, leading to a larger growth rate.
In figure 6, the real frequency and growth rate versus k_\theta\rho_{\rm{s}} with \kappa_n=1.97 , 2.61 , 3.07 and 3.88 are presented, which correspond to about 0.8\kappa_{n0} , 1.0\kappa_{n0} , 1.2\kappa_{n0} and 1.5\kappa_{n0} , respectively. From figure 6(a), it is seen that the real frequency of ITG instability in the adiabatic electron model decreases as \kappa_n increases for a fixed k_\theta\rho_{\rm{s}} ; the tendencies are opposite to those of \kappa_{T_{\rm{i}}} , shown in figure 4(a). Note that the driving terms due to the spatial inhomogeneity of equilibrium distribution for the ITG instability are proportional to \kappa_n+ \kappa_{T_{\rm{i}}}(E_{\rm{res}}-3/2) , with E_{\rm{res}} being the resonant energy. Obviously, when E_{\rm{res}}<3/2 , the contributions of \kappa_n and \kappa_{T_{\rm{i}}} to the real frequency are opposite. In the kinetic electron model, for each \kappa_n , the ITG instability mainly dominates in the smaller k_\theta\rho_{\rm{s}} region. Compared to the results in the adiabatic model, the real frequency of ITG instability shifts towards the electron diamagnetic drift direction by enlarging \kappa_n , and the dependence on k_\theta\rho_{\rm{s}} is sharper. In the larger k_\theta\rho_{\rm{s}} region, the dominant instability can transform from ITG instability to TEM, and a larger \kappa_n corresponds to a larger transform value ( k_\theta\rho_{\rm{s}})_{\rm{TR}} . Analogously, in the higher k_\theta\rho_{\rm{s}} region, the contributions of the ion NAR term become smaller due to the FLR effects, which makes the excitation of TEM possible. In addition, for \kappa_n=3.07 and 3.88 , TEM dominates in the smaller k_\theta\rho_{\rm{s}} region, and the range of the TEM spectrum for \kappa_n=3.88 is wider.
In figure 6(b), the growth rate in the adiabatic electron model increases firstly and then decreases with k_\theta\rho_{\rm{s}} increased for each \kappa_n , and the maximum growth rates for each \kappa_n are comparable. As \kappa_n increases from 1.97 to 3.88, the k_\theta spectrum for the ITG instability is extended from k_\theta\rho_{\rm{s}}=0.9 to 1.1, and the peak position shifts from k_\theta\rho_{\rm{s}}=0.6 to 0.8. However, the growth rate in the kinetic electron model is much larger than that in the adiabatic electron model for each \kappa_n . Furthermore, the maximum growth rate increases significantly with the increment of \kappa_n . For example, the maximum growth rate is larger by almost a factor of 2 for \kappa_n=1.97 and a factor of 5 for \kappa_n=3.88 . Note that the maximum growth rate appears in the ITG-dominant region, and it seems that \kappa_n shows a strong destabilizing effect on the ITG instability when taking the kinetic electron effects into account. One possible explanation for this feature is that the electron NAR term becomes larger due to the larger \kappa_n ; in other words, the electron AR term becomes relatively weaker, then the growth rate of ITG instability shows a significant increment. In addition, the growth rate of TEM is smaller than that of ITG instability, except for the case with \kappa_n=1.97 , where the maximum growth rates of TEM and ITG instability are comparable.
Generally, the ITG instability is also called \eta_{\rm{i}} mode, since the parameter \eta_{\rm{i}}= \kappa_{T_{\rm{i}}}/ \kappa_n dominates the character of ITG instability. However, the effects of \kappa_{T_{\rm{i}}} and \kappa_n on the ITG instability separately analyzed above show that both \kappa_{T_{\rm{i}}} and \kappa_n can destabilize the ITG instability, so it is interesting to have a look at the effects of \eta_{\rm{i}} on the ITG instability for the ITER baseline scenario.
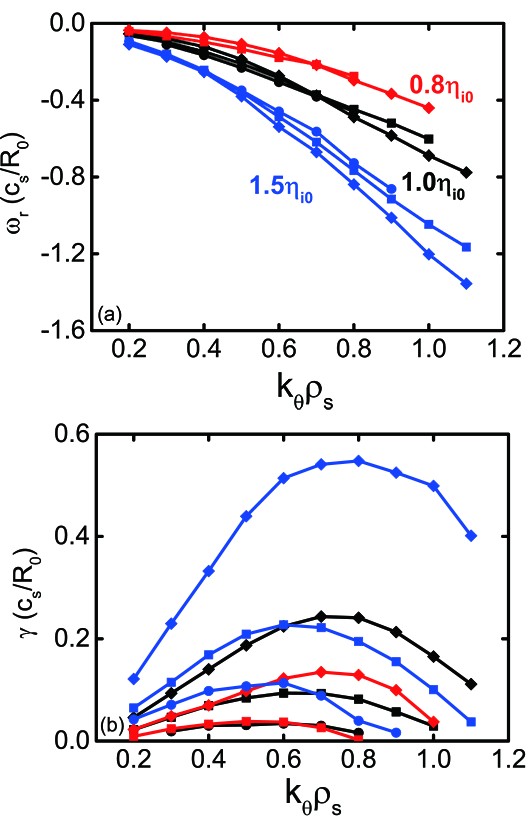
In figure 7, the real frequency and growth rate versus k_\theta\rho_{\rm{s}} in the adiabatic electron model are depicted for \eta_{\rm{i}}=0.8\eta_{\rm{i0}} , 1.0\eta_{\rm{i0}} and 1.5\eta_{\rm{i0}} . \eta_{\rm{i0}}=\kappa_{T_{\rm{i0}}}/\kappa_{n0} is the nominal value. Among each \eta_{\rm{i}} , three \kappa_n values of 1.97 , 2.61 and 3.88 , which correspond to 0.8\kappa_{n0} , 1.0\kappa_{n0} and 1.5\kappa_{n0} , respectively, are adopted. Clearly, the curves for the real frequency in figure 7(a) can be divided into three groups based on the value of \eta_{\rm{i}} . The real frequency becomes significantly larger as \eta_i increases. For \eta_{\rm{i}}=0.8\eta_{\rm{i0}} , the real frequency is almost not affected by \kappa_n ; for \eta_{\rm{i}}=1.5\eta_{\rm{i0}} , the effect of \kappa_n is also weak. The growth rate is shown in figure 7(b). For a fixed \kappa_n (the lines labeled by the same symbol but different colors), it is found that a larger \eta_{\rm{i}} corresponds to a larger growth rate. Similarly, for a fixed \eta_{\rm{i}} (the lines labeled by the same color but different symbols), a larger \kappa_n corresponds to a larger growth rate. Obviously, in these two situations, the larger growth rates originate from the \kappa_{T_{\rm{i}}} effects, which are consistent with the results in figure 4(b). In addition, the curves for the growth rate can be divided into four groups, which correspond to a maximum growth rate of about 0.04c_{\rm{s}}/R_0 , 0.10c_{\rm{s}}/R_0 , 0.22c_{\rm{s}}/R_0 and 0.55c_{\rm{s}}/R_0 , respectively. In each group, the values of \eta_{\rm{i}} and \kappa_n are different among the different curves, but the value of \kappa_{T_{\rm{i}}} is almost the same. The larger \kappa_{T_{\rm{i}}} is, the larger the growth rate is. In the adiabatic electron model, the real frequency and growth rate of ITG instability are mainly affected by \eta_{\rm{i}} and \kappa_{T_{\rm{i}}} , respectively.
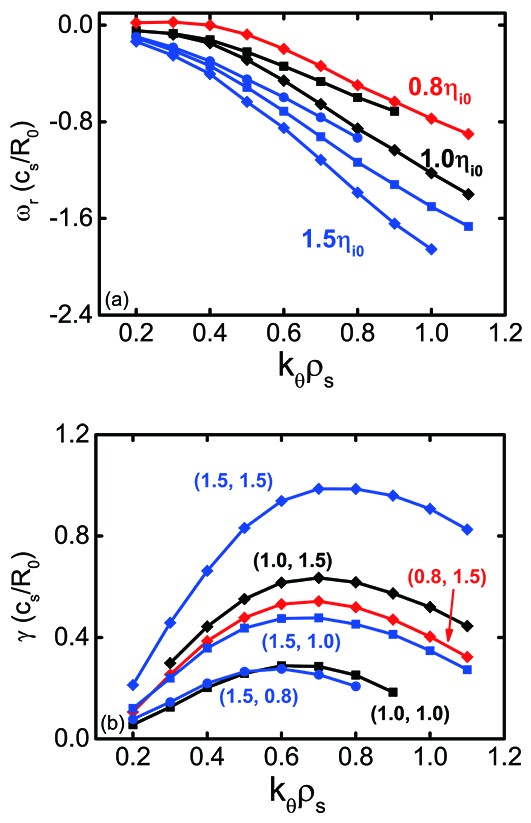
The situations with the kinetic electron model are shown in figure 8. Since the scanning results above show that TEM dominates in a narrower parameter range, we do not display the curves of TEM in figure 8, and only discuss the effects of \eta_{\rm{i}} on the ITG instability for simplicity. It is seen from figure 8(a) that the real frequency increases with the increment of \eta_{\rm{i}} , and the effect of \kappa_n on the real frequency is obvious. In figure 8(b), for better clarification, we label the curves with (x,y) , which denotes that \eta_{\rm{i}}=x\cdot\eta_{\rm{i0}} and \kappa_n=y\cdot\kappa_{n0} , then \kappa_{T_{\rm{i}}}=xy\cdot\kappa_{T_{\rm{i0}}} . It is clear that the growth rate becomes larger when \eta_{\rm{i}} increases for a fixed \kappa_n , as well as when \kappa_n increases for a fixed \eta_{\rm{i}} , which are the same as the results found with the adiabatic electron model. However, the dependence of the growth rate on \kappa_{T_{\rm{i}}} is not similar to that in the adiabatic electron model. Since the growth rate increases with the increment of \kappa_{T_{\rm{i}}} or \kappa_n , the growth rate in the case with small \eta_{\rm{i}} and large \kappa_n could be larger than that with large \eta_{\rm{i}} and relatively small \kappa_{T_{\rm{i}}} . For example, the growth rate labeled by the curve (1.0,1.0) (with \kappa_{T_{\rm{i}}}=1.0\kappa_{T_{\rm{i0}}} ) is close to that with (1.5,0.8) ( \kappa_{T_{\rm{i}}}=1.2\kappa_{T_{\rm{i0}}} ), but is quite a lot smaller than that with (0.8,1.5) ( \kappa_{T_{\rm{i}}}=1.2\kappa_{T_{\rm{i0}}} ). Whether the growth rate increases or not depends on the competition between the increment of \kappa_{T_{\rm{i}}} and \kappa_n .
In figure 9, the real frequency and growth rate versus k_\theta\rho_{\rm{s}} for \tau=0.96 , 1.2 and 2.4 in the adiabatic electron model are presented. The solid and dashed lines denote that \tau is varied by separately changing T_{\rm{e}} and T_{\rm{i}} , respectively. It is clearly seen that the real frequency and growth rate normalized by c_{\rm{s}}/R_0 are almost the same in the cases of separately changing T_{\rm{e}} and T_{\rm{i}} . In other words, the normalized real frequency and growth rate depend on the value of \tau instead of T_{\rm{e}} or T_{\rm{i}} . This feature is indeed easy to observe when one notes that it is \tau instead of T_{\rm{e}} or T_{\rm{i}} that appears in the dispersion relation, as shown in equations (9a) and (9b). It should be noted that c_{\rm{s}}/R_0 varies for different T_{\rm{i}} , thus the frequencies with units of Hz are not the same when separately changing T_{\rm{e}} and T_{\rm{i}} . From figure 9(a), it is seen that the dependence of the real frequency on k_\theta\rho_{\rm{s}} for \tau=0.96 is quite similar to that for \tau=1.2 . As \tau reaches up to 2.4, the real frequency changes little in the range of k_\theta\rho_{\rm{s}}\leqslant0.5 compared to the case for \tau=1.2 , and then becomes larger with the increment of k_\theta\rho_{\rm{s}} . From figure 9(b), it is shown that, for each \tau , the normalized growth rate increases first and then decreases by enlarging k_\theta\rho_{\rm{s}} , and the most unstable mode appears at around k_\theta\rho_{\rm{s}}=0.7 . In addition, the maximum growth rate becomes significantly larger by increasing \tau . Clearly, the large \tau reduces the magnitude of the electron AR term, which leads to the large growth rate of the ITG instability. This feature is somewhat analogous to the reduction of the electron AR term by introducing the trapped electron fraction.
In addition, the normalized real frequency and growth rate versus \tau for k_\theta\rho_{\rm{s}}=0.4 , 0.7 and 0.9 in the adiabatic electron model are shown in figure 10. It is seen that the effects of \tau on different k_\theta\rho_{\rm{s}} are somewhat different. In detail, as \tau increases from 0.96 to 3.6 , the normalized real frequency for k_\theta\rho_{\rm{s}}=0.4 is almost unchanged. The normalized real frequency for k_\theta\rho_{\rm{s}}=0.7 increases from −0.34 to −0.46 , and the increment for k_\theta\rho_{\rm{s}}=0.9 is more obvious, from −0.50 to −0.73. On the other hand, the growth rate for each mode increases by enlarging \tau . The increment for the most unstable mode is the most significant, which indicates that the ITG instability is strongly destabilized by \tau . We can also note that when the mode frequency is normalized by \omega_{*{\rm{e}}}=k_\theta T_{\rm{e}}/eBL_n , the real frequency and growth rate show similar dependences on T_{\rm{e}}/T_{\rm{i}} to the previous results [33].
In figures 11 and 12, the situations for the kinetic electron model are shown. The parameters are the same as those in figures 9 and 10, respectively. Analogously, the normalized real frequency and growth rate are almost the same when separately changing T_{\rm{e}} and T_{\rm{i}} . Note that in the electron perturbed distribution function shown in equation (9b), the electron driving term and the bounce-averaged drift frequency in the NAR term are proportional to \tau with the normalization of c_{\rm{s}}/R_0 , thus it is \tau instead of T_{\rm{e}} that appears in the dispersion relation in the kinetic electron model. The real frequencies of ITG instability seem to be slightly changed as \tau varies, as is clarified by the character of k_\theta\rho_{\rm{s}}=0.4 , 0.7 and 0.9 in figure 12(a). Additionally, it is seen that TEM dominates with two parameter regimes. One is in the higher k_\theta\rho_{\rm{s}} region, and the other is in the lower k_\theta\rho_{\rm{s}} region accompanied with a larger \tau . For example, it is shown in figure 11(a) that TEM dominates in the range of k_\theta\rho_{\rm{s}}<0.5 for \tau=2.4 . In addition, the dominant instability for k_\theta\rho_{\rm{s}}=0.4 changes from ITG to TEM when enlarging \tau from about 1.5 to about 1.8 , as shown in figure 12(a). In the former regime, the transition wavenumber ( k_\theta\rho_{\rm{s}})_{\rm{TR}} becomes larger with larger \tau . Note that the ITG instability is destabilized by \tau , thus for large \tau , k_\theta\rho_{\rm{s}} should be large enough to reduce the ion NAR term due to the FLR effects. A possible explanation for the latter feature is that the TEM-driving source in the electron NAR term relates to \omega_{*{\rm{e}}}R_0/c_{\rm{s}}\propto k_\theta\rho_{\rm{s}}\tau , and the larger \tau is more beneficial for the excitation of TEM when fixing k_\theta\rho_{\rm{s}} .
Compared to figure 9(b), the growth rate of ITG instability shown in figure 11(b) is significantly larger than that in the adiabatic electron model for each \tau . Similarly, the growth rate peaks at around k_\theta\rho_{\rm{s}}=0.7 . The growth rates of TEM are notably smaller than those of ITG. When \tau=2.4 , the growth rates for 0.4\leqslant k_\theta\rho_{\rm{s}}\leqslant0.8 are close to each other. The growth rates versus \tau for k_\theta\rho_{\rm{s}}=0.4 , 0.7 and 0.9 are shown in figure 12(b) for further illustration. It is seen that the growth rate for each k_\theta\rho_{\rm{s}} increases with the increment of \tau . When \tau<2.4 , the maximum growth rate appears at around k_\theta\rho_{\rm{s}}=0.7 . However, when \tau>2.4 , the maximum growth rate shifts to k_\theta\rho_{\rm{s}}=0.4 . It is seen in figure 12(a) that TEM dominates for k_\theta\rho_{\rm{s}}=0.4 when \tau>2.4 , which indicates that the transition from ITG-dominant to TEM-dominant could take place by increasing \tau . Note that the electron temperature can be effectively raised with various auxiliary heating regimes, and the dominant instability may be transformed during the heating process. Realizing the transform of the dominant instability due to the increase of \tau would be helpful for the analysis of related turbulent transport.
In this section, the nonlinear evolutions of electrostatic instabilities on the ITER baseline scenario are studied. The radial computational domain is set as (0.4a,0.6a) , which is about 146\rho_{\rm{s}} . The grid resolutions are adopted as (N_\psi,N_\theta, N_{v_\parallel},N_\mu)=(256,16,64,16) . The perturbed distribution on the radial boundary of the computational domain is set as zero, and a damping buffer region of 14\rho_{\rm{s}} near the radial boundary is adopted. In each nonlinear simulation, we choose 32 toroidal modes, which are set as {n}= [0\; 1\; 2\; \cdots\; 31]\times {n}_0 with {n}_0 a constant. Clearly, the maximum poloidal wavenumber k_{\theta,\max}=31 {n}_0q(r_0)/r_0 kept in the nonlinear simulation can be adjusted by {n}_0 . By choosing the appropriate {n}_0 , both the linearly unstable ITG instability and TEM can be included in the nonlinear simulation.
In figure 13, the time evolutions of heat diffusivities for ions and electrons are shown. Three typical \kappa_{T_{\rm{i}}} values of 4.11 , 5.09 and 7.49 are chosen. In the kinetic electron model, it is seen from figure 4(a) that TEM dominates when \kappa_{T_{\rm{i}}}=4.11 , ITG dominates when \kappa_{T_{\rm{i}}}=7.49 , and an ITG–TEM transition occurs in the poloidal spectrum when \kappa_{T_{\rm{i}}}=5.09 . We recall that the maximum growth rate shown in figure 4(b) increases significantly with the increment of \kappa_{T_{\rm{i}}} , and this increment leads to two results. On one hand, the saturated heat diffusivity for ions becomes larger for larger \kappa_{T_{\rm{i}}} . In detail, for \kappa_{T_{\rm{i}}}=4.11 , 5.09 and 7.49 , the saturated heat diffusivity for ions is about \chi_{\rm{i}}=2.61\; {\rm{m}}^2/{\rm{s}} , 4.88\; {\rm{m}}^2/{\rm{s}} and 8.72\; {\rm{m}}^2/{\rm{s}} , respectively. On the other hand, the turbulence enters the linear stage and nonlinear stage earlier with larger \kappa_{T_{\rm{i}}} . For each \kappa_{T_{\rm{i}}} , the time evolution of heat diffusivity for electrons shows a similar tendency to that for ions in the kinetic model, and the value is about half of that for ions in the saturation stage. In the adiabatic electron model, only the heat diffusivity for ions is shown. It is seen that the heat diffusivity for ions in the adiabatic electron model is quite a lot smaller than that in the kinetic electron model, which is about \chi_{\rm{i}}=0.97\; {\rm{m}}^2/{\rm{s}} and 2.82\; {\rm{m}}^2/{\rm{s}} for \kappa_{T_{\rm{i}}}=5.09 and 7.49 , respectively. The case for \kappa_{T_{\rm{i}}}=4.11 is not shown due to its smaller value of \chi_{\rm{i}} . In addition, it needs more time for the turbulence to the enter the linear and nonlinear stages. Analogously, the heat diffusivity for ions increases as \kappa_{T_{\rm{i}}} increases. In addition, it is seen that the heat diffusivities oscillate more rapidly in the kinetic electron model.
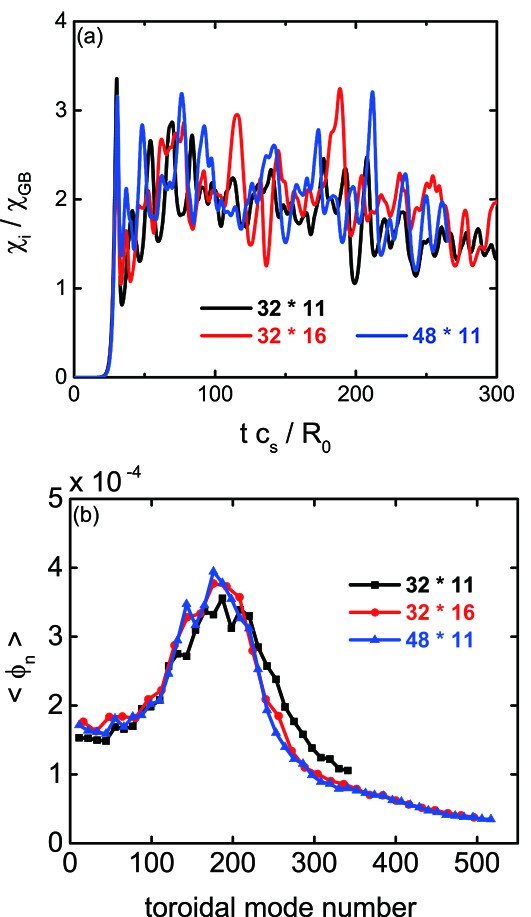
We mention that the poloidal wavenumber is truncated with ( k_\theta\rho_{\rm{s}})_{\rm{max}}=0.9 in the nonlinear simulations in figure 13. However, it is clearly seen from figure 4(b) that the growth rate in the larger k_\theta\rho_{\rm{s}} region is comparable with the growth rate in the smaller k_\theta\rho_{\rm{s}} region, especially for the cases with \kappa_{T_{\rm{i}}}=5.09 and 4.11 . Whether or not the saturated heat diffusivity is affected by the truncation of ( k_\theta\rho_{\rm{s}})_{\rm{max}} should be clarified. Figure 14 shows the comparison of the time evolution of ion heat diffusivity (normalized by \chi_{\rm{GB}}=c_{\rm{s}}\rho_{\rm{s}}^2/a ) and the flux-averaged perturbed potential with different toroidal mode number with \kappa_{T_{\rm{i}}}=5.09 in the kinetic electron model, where the truncations of the poloidal spectrum are adopted as ( k_\theta\rho_{\rm{s}})_{\rm{max}}=0.9 and ( k_\theta\rho_{\rm{s}})_{\rm{max}}=1.4 , respectively. In particular, for the case of ( k_\theta\rho_{\rm{s}})_{\rm{max}}=1.4 , we choose 32 modes with {n}_0=16 and 48 modes with {n}_0=11 , respectively. The Fourier decomposition of perturbed potential is \delta\phi(r,\alpha,\theta)=\sum\limits_n\phi_n{\rm{e}}^{-{\rm{i}}n\alpha} , and \langle\phi_n\rangle denotes the flux average of \phi_n in the radial and poloidal directions. It is seen from figure 14(a) that the time evolutions of ion heat diffusivities in the linear stage ( tc_{\rm{s}}/R_0<30 ) with these two different ( k_\theta\rho_{\rm{s}})_{\rm{max}} are quite similar, and the values of ion heat diffusivities in the nonlinear saturation stage are close to each other, although the time oscillations with different ( k_\theta\rho_{\rm{s}})_{\rm{max}} are somewhat different. In figure 14(b), we draw the saturated perturbed potential with the time average from 50R_0/c_{\rm{s}} to 200R_0/c_{\rm{s}} . Some obvious features can be easily captured. Firstly, the \langle\phi_n\rangle spectra in the two cases of ( k_\theta\rho_{\rm{s}})_{\rm{max}}=1.4 are quite similar, but somewhat different from the case of ( k_\theta\rho_{\rm{s}})_{\rm{max}}=0.9 in the range of {n}>240 . Secondly, in these three cases, the largest magnitudes of components appear between {n}\approx150 and 220 , which correspond to k_\theta\rho_{\rm{s}}\approx0.4 -0.6 . Obviously, the fluctuations in this region govern the turbulent transport. Note that the peak of the saturated magnitude spectrum is downshifted from that of the linear growth rate, which indicates that the energy cascades from the modes with larger wavenumber to the modes with lower wavenumber in the ITG-dominant region [34].
In figure 15, the time evolutions of \langle\phi_n\rangle for some typical toroidal modes in the case with 32 modes and {n}_0=16 are shown for the purpose of further illustrating the contributions of fluctuations with higher k_\theta\rho_{\rm{s}} to the turbulent transport. It is seen that the fluctuations with moderate toroidal mode number {n}\sim208-240 grow the fastest in the linear stage, which agrees well with the fact that the linear growth rates are the largest at around k_\theta\rho_{\rm{s}}\sim0.6 -0.7 . The zonal flow is then excited and grows at a higher growth rate. At around tc_{\rm{s}}/R_0=24 , the magnitude of the zonal flow exceeds the fluctuations, and then both the zonal flow and fluctuations reach the saturation stage. The exponential fitting for {n}=0 and 240 in the linear stage shown in the zoomed-in plot gives \gamma_{\rm{fit}}=0.69c_{\rm{s}}/R_0 for {n}=0 and \gamma_{\rm{fit}}=0.34c_{\rm{s}}/R_0 for {n}=240 . The linear growth rate for the zonal flow is about two times larger than the dominant fluctuation \phi_{{n}=240} , which suggests that the zonal flow is passively generated by the three-wave coupling [35, 36]. In addition, it is seen that the linear stages for the fluctuations with a lower mode number of {n}=16 and {n}=32 are almost the same as those with a higher mode number of {n}=432 and {n}=464 . These modes reach their saturation stages when the modes of {n}=208 and {n}=240 are saturated. Furthermore, the linear growth rates for these modes are close to that of zonal flow, and are significantly larger than those of the {n}=208 and {n}=240 modes. The linear results in figure 4 show that the growth rate for k_\theta\rho_{\rm{s}}=0.1 is quite a lot lower than that for k_\theta\rho_{\rm{s}}=0.7 , and there is no doubt that the linear stages for {n}=16 and {n}=32 in figure 15 are not linearly driven by themselves. Instead, the fluctuations with lower mode numbers of {n}=16 and {n}=32 , as well as fluctuations with higher {n}=432 and {n} =464 , are nonlinearly driven by the fluctuations with moderate mode numbers such as {n}=208 and {n}=240 via the mode coupling process.
Additionally, as shown in figure 4(b), the poloidal spectrum of the TEM with \kappa_{T_{\rm{i}}}=4.11 shows that the growth rate continuously increases with the poloidal wavenumber k_\theta , without having a clear peak point around the ion-scale wavelength region k_\theta\rho_{\rm{s}}\sim1.0 . Analogous to the treatment with \kappa_{T_{\rm{i}}}=5.09 , we take another nonlinear simulation for \kappa_{T_{\rm{i}}}=4.11 by changing {n}_0 from 11 to 16 , then ( k_\theta\rho_{\rm{s}})_{\rm{max}} is changed from 0.9 to 1.4. Unsurprisingly, the time evolution of ion heat diffusivities and the magnitudes of flux-averaged perturbed potential of different toroidal mode number show similar tendencies to those in figure 14; that is, the contribution from the fluctuations with k_\theta\rho_{\rm{s}}>1.0 to the turbulent transport can be neglected. In addition, from the viewpoint of the mixing length approximation model, the widely used turbulent diffusion coefficient is written as [37]
| D_\perp=\gamma/k_\perp^2. | (11) |
Although the growth rates for the modes of k_\theta\rho_{\rm{s}}>0.9 are comparable with (or even larger than) those of k_\theta\rho_{\rm{s}}<0.9 , the mixing length decreases, and a larger k_\perp leads to a smaller D_\perp , as well as a smaller heat diffusivity.
Here, we mention that the nonlinear saturation of TEM is found to be related to the zonal flow or the zonal density, and that the roles of zonal flow and zonal density are parameter-sensitive [38, 39]. It is interesting to take a look at the nonlinear saturation mechanism of TEM on the ITER baseline scenario, and this issue remains as a future work.
Figure 16 shows the time-spatial contour structure of the ion heat transport coefficient \chi_{\rm{i}}/\chi_{\rm{GB}} at the nonlinear stage with the adiabatic and kinetic electron models, respectively. The buffer regions are not presented. Compared to the case in the adiabatic electron model, the heat transport coefficient in the kinetic electron model presents a larger value at different radii. In addition, the radial structure is finer and the time oscillation is more rapid. The former feature is indeed expected from the larger saturated magnitude of perturbed potential in the kinetic electron model, and the latter feature indicates that the turbulent eddies due to the self-generated zonal flow are smaller.
Figure 17(a) shows the radial profiles of saturated particle fluxes in the kinetic electron model with \kappa_{T_{\rm{i}}}=4.11 , 5.09 and 7.49 . \Gamma_{\rm{GB}}=n_0c_{\rm{s}}(\rho_{\rm{s}}/a)^2 . It is seen that for each \kappa_{T_{\rm{i}}} , the particle flux is outward. The outward particle flux within r=0.5a slightly decreases, and then drops notably in the r>0.5a region. With the increment of \kappa_{T_{\rm{i}}} , the outward particle flux increases. Clearly, the larger radial particle flux is expected from the stronger saturated turbulence, which is due to the larger linear growth rate. Figure 17(b) shows the profiles of the zonal radial electric field E_r for different \kappa_{T_{\rm{i}}} . It is seen that E_r for \kappa_{T_{\rm{i}}}=4.11 and 5.09 are quite small. When \kappa_{T_{\rm{i}}} increases to 7.49 , E_r is mainly positive, and exhibits a relatively large value.
The gyrokinetic calculations show that the zonal radial electric field driven by the electrostatic turbulence satisfies [40, 41]
| \begin{split}\partial_tE_r=&-\frac1{ne}\partial_r\bigg[\frac1r\partial_r\Big(r\frac23Q_r\Big)\bigg] +\frac1{ \varepsilon_{\rm{r}}}B_{\rm{T}}\frac1{nm}\frac1r\partial_r\big(r\Pi_{r\theta}\big) -\\&B_{\rm{P}}\frac1{nm}\frac1r\partial_r\big(r\Pi_{r\zeta}\big). \end{split} | (12) |
Here, B_{\rm{T}} and B_{\rm{P}} are the toroidal and poloidal magnetic fields, respectively. Q_r is the turbulent-driven energy flux, and \Pi_{r\zeta}\equiv nm\langle\delta v_r\delta v_\zeta\rangle is the turbulent toroidal Reynolds stress, with \delta v_r and \delta v_\zeta denoting the radial and toroidal components of the fluctuated {\boldsymbol{E}}\times{\boldsymbol{B}} drift, respectively. \Pi_{r\theta}\equiv nm\langle\delta v_r\delta v_\theta\rangle denotes the turbulent poloidal Reynolds stress (PRS), where \delta v_\theta is the poloidal component of {\boldsymbol{E}}\times{\boldsymbol{B}} drift. \varepsilon_{\rm{r}}=1+1.64q^2/\sqrt{\epsilon} is the shielding factor due to the toroidal effects [42], and \epsilon is the inverse aspect ratio. Note that the turbulent radial electric field originates from the finite orbit width effects; thus, in the ITG-dominant turbulence, the finite orbit width for electrons can be assumed to be zero, and then only the turbulent fluxes for ions are included in equation (12). In addition, the simulations carried out in the adiabatic electron model with the CBC parameters focused on the contributions of turbulent energy flux and turbulent toroidal Reynolds stress on the zonal radial electric field, which revealed that the zonal radial electric field is dominantly driven by the energy flux, and contributions from the toroidal Reynolds stress term can be neglected [43]. In the following analysis, we mainly focus on the contributions of the energy flux term and the PRS term on the radial electric field.
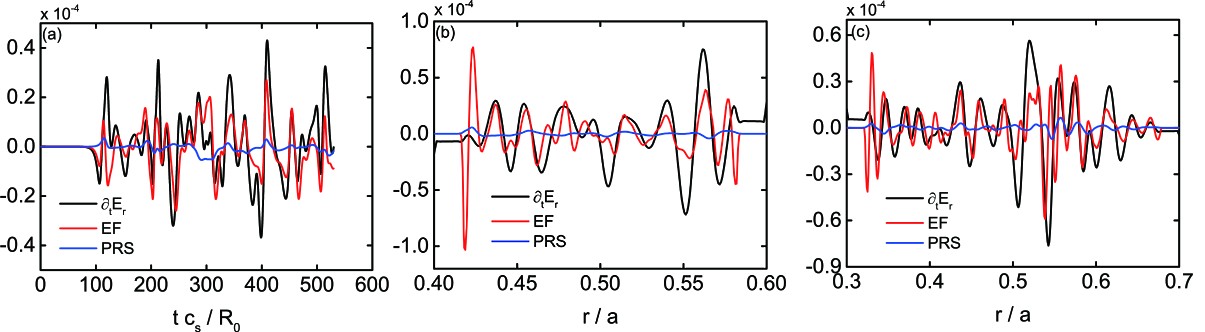
Figure 18 shows the comparison of the turbulent radial electric field term with the turbulent energy flux and PRS terms in the case of adopting the adiabatic electron model. The physical quantities are normalized by c_{\rm{s}}^2B_0/R_0 . In figure 18(a), it is shown that the time evolution of the energy flux term matches the electric field term well, and the contribution of the PRS term is quite small due to the toroidal shielding effect. Comparison of the radial distribution at the nonlinear saturated stage with t=324R_0/c_{\rm{s}} in figure 18(b) also shows the similarity between the energy flux term and the electric field term. We mention that the nonphysical oscillations of the turbulent energy flux term near the left and right boundaries are due to the existence of the buffer region. Another nonlinear simulation with the same parameters as those adopted in figure 18(b), with the exception that the radial computation domain is extended from (0.4a,0.6a) to (0.3a,0.7a) , is carried out. Correspondingly, the radial grid mesh is set as N_\psi=400 . Figure 18(c) shows the spatial profiles of the turbulent terms at the same time interval t=324R_0/c_{\rm{s}} . It is clearly seen that the turbulent energy flux term matches the electric field term well in the region between 0.4a and 0.6a ; similarly, the nonphysical oscillation of the turbulent energy flux term appears around the left buffer region.
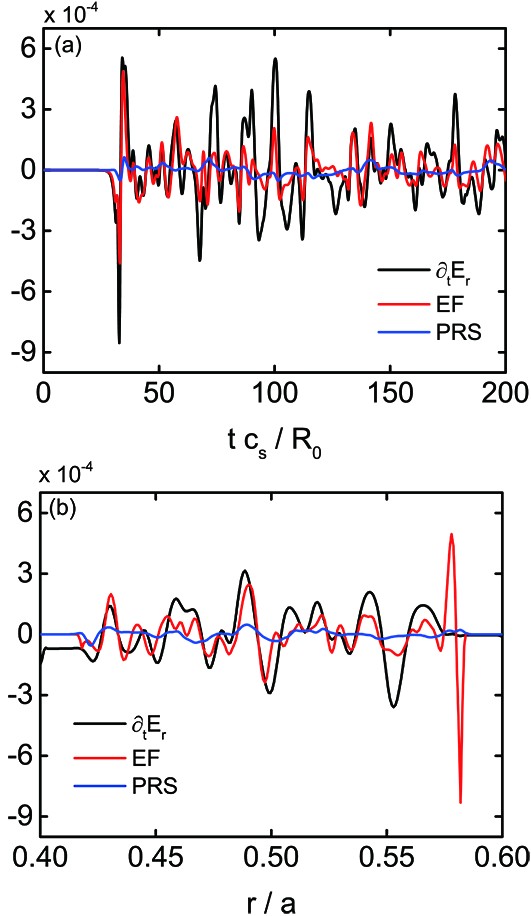
Figure 19 shows the comparison of the turbulent radial electric field term with the turbulent energy flux and PRS terms in the case with the kinetic electron model adopted. In figure 19(a), the time evolution of the turbulent-driven terms at r=0.5a shows more rapid oscillation and larger amplitude compared with those in the adiabatic electron model. In the earlier nonlinear stage, the time variation of the turbulent energy flux term is associated with the turbulent electric field term, and the oscillation magnitude is also comparable. However, in the nonlinear saturated stage, especially when tc_{\rm{s}}/R_0>60 , a relatively large discrepancy between the turbulent energy flux term and the turbulent electric field term is observed. According to the turbulence simulations using the GTC, the particle fluxes of kinetic electrons and ions exhibit ambipolar characteristics when the spatial scale is beyond ion-FLR, and the kinetic electron contribution to zonal guiding-center charge density can partially cancel with that of the ion species [44]. Whether this cancellation is important for the discrepancy observed in figure 19(a) deserves further investigation. From figure 19(b), it is seen that the radial distribution of turbulent energy flux matches with the turbulent electric field term to some extent, and the turbulent PRS contribution can be neglected as well. We mention that the unphysical oscillation at around r/a=0.57 is due to the existence of the buffer region.
From figures 18 and 19, it is concluded that the turbulence-driven zonal radial electric fields in both the adiabatic and kinetic electron models show similar characteristics; that is, the zonal radial electric field is mainly driven by the turbulent energy flux, and the contribution of the turbulent PRS is relatively small in the ITER baseline scenario. However, it should be noted that the turbulent PRS is a well-known mechanism for driving the zonal radial electric field [45–48]. It is an interesting issue that furthers our understanding of the regime where the turbulent energy flux term dominates and where the turbulent PRS term dominates.
In conclusion, by separately adopting the adiabatic and kinetic electron models in the gyrokinetic code NLT, the kinetic electron effects on the linear frequency and nonlinear transport driven by the electrostatic instabilities on the ITER baseline scenario are numerically studied.
The linear simulations focus on the dependence of linear frequency on the plasma parameters, such as the temperature gradient \kappa_{T_{\rm{i,e}}}=R/L_{T_{\rm{i,e}}} , the density gradient \kappa_n=R/L_n and the temperature ratio \tau=T_{\rm{e}}/T_{\rm{i}} . In the kinetic electron model, for the nominal values of \kappa_{T_{\rm{i}}}=5.09 and \kappa_{T_{\rm{e}}}=6.23 , the ITG instability and TEM dominate in the range of k_\theta\rho_{\rm{s}}\leqslant0.9 and k_\theta\rho_{\rm{s}}>0.9 , respectively. The maximum growth rate appears at around k_\theta\rho_{\rm{s}}=0.7 , which is located in the ITG-dominant region. The maximum growth rate value is 0.30c_{\rm{s}}/R_0 , which is enlarged by a factor of about 3 compared to that in the adiabatic electron model. The real frequency shifts towards the electron diamagnetic drift direction by decreasing \kappa_{T_{\rm{i}}} or increasing \kappa_{T_{\rm{e}}} . Specifically, when \kappa_{T_{\rm{i}}}\leqslant4.11 or \kappa_{T_{\rm{e}}}\geqslant9.00 , TEM dominates in the whole range of k_\theta\rho_{\rm{s}}<1.2 . The growth rate of ITG instability increases obviously by enlarging \kappa_{T_{\rm{i}}} , while it is hardly affected by \kappa_{T_{\rm{e}}} . Meanwhile, the TEM is destabilized by \kappa_{T_{\rm{e}}} but stabilized by \kappa_{T_{\rm{i}}} . The transition from ITG-dominant to TEM-dominant also occurs by varying \kappa_n when the kinetic electron effects are considered. The larger \kappa_n is, the larger the turning point ( k_\theta\rho_{\rm{s}})_{\rm{TR}} is. In the adiabatic electron model, the maximum growth rates of ITG instability are close for different \kappa_n ; however, the maximum growth rates in the kinetic electron model increase significantly by increasing \kappa_n . In the kinetic electron model, since the growth rates of ITG instability increase with the increment of \kappa_{T_{\rm{i}}} or \kappa_n , the growth rate with smaller \eta_{\rm{i}} could be larger than that with larger \eta_{\rm{i}} , and depends on the competition between the increment of \kappa_{T_{\rm{i}}} and \kappa_n . Scanning of the temperature ratio \tau indicates that the normalized real frequency and growth rate for both ITG instability and TEM depend on the value of \tau , rather than the value of T_{\rm{i}} or T_{\rm{e}} , in both the adiabatic and the kinetic electron model. In the kinetic electron model, the ITG instability is strongly destabilized by \tau , and TEM dominates in the higher and the lower k_\theta\rho_{\rm{s}} region accompanied with larger \tau , which infers that the occurrence of the transition from ITG-dominant to TEM-dominant in the lower k_\theta\rho_{\rm{s}} region could be easily realized by increasing \tau .
In the nonlinear simulations, three typical cases with values of \kappa_{T_{\rm{i}}}=4.11 , 5.09 and 7.49 are presented. In both the adiabatic and kinetic electron models, the ion heat diffusivity in the saturated stage of turbulence increases with the increment of \kappa_{T_{\rm{i}}} . Compared to the cases in the adiabatic electron model, the value of ion heat diffusivity for each \kappa_{T_{\rm{i}}} is quite a lot larger in the kinetic electron model, and the turbulence reaches its saturated stage earlier. Three special nonlinear simulations, in which the maximum poloidal wavenumber (k_\theta\rho_{\rm{s}})_{{\rm{max}}} is extended from 0.9 to 1.4 , are carried out with the kinetic electron model for \kappa_{T_{\rm{i}}}=5.09 . The ion heat diffusivities in these two (k_\theta\rho_{\rm{s}})_{{\rm{max}}} cases are close to each other, indicating that the contributions from the modes of k_\theta\rho_{\rm{s}}>0.9 to the transport level can be neglected. The toroidal spectrum analysis shows that the magnitude of fluctuated potential in the saturated stage peaks in the ITG-dominated region, which presents a similar tendency to the dependence of the growth rate on k_\theta\rho_{\rm{s}} . In addition, the radial structure of ion heat transport coefficients in the kinetic electron model becomes finer, and the time oscillation is more rapid. The particle flux evaluated in the kinetic electron model is calculated to be outward for each \kappa_{T_{\rm{i}}} , and the outward particle flux increases with the increment of \kappa_{T_{\rm{i}}} . The zonal radial electric field for \kappa_{T_{\rm{i}}}=4.11 and 5.09 is quite small. When \kappa_{T_{\rm{i}}} increases to 7.49, the zonal radial electric field is mainly positive, and exhibits a relatively large value in a wide radial domain. Based on the gyrokinetic theory, contributions of the turbulent energy flux and the turbulent PRS to the zonal radial electric field are evaluated in both the adiabatic and kinetic electron models. It is found that, in the adiabatic electron model, the zonal radial electric field is mainly driven by the turbulent energy flux, and the contribution of turbulent PRS is quite small due to the toroidal shielding effect. In the kinetic electron model, the turbulent energy flux term matches well with the zonal radial electric field term in the linear and early nonlinear stages, while the turbulent energy flux is not strong enough to drive the zonal radial electric field in the nonlinear saturated stage. The kinetic electron effects on the mechanism of the turbulence-driven zonal radial electric field should be further investigated.
Quantitatively speaking, consideration of the kinetic electron effects leads to a significant increment of the maximum growth rate of dominant ITG instability and the associated nonlinear ion heat transport coefficient, as well as the time-spatial contour structure. There is no doubt that the kinetic electron effects play important roles on the turbulent transport. Moreover, the realistic transport picture for the ITER baseline scenario also depends on various physical effects, such as the effects of energetic particles, the ion–ion collisions and the electromagnetic fluctuation. These issues are left for future work.
The data that support the findings of this study are available from the corresponding author upon reasonable request.
The authors thank Prof. Shaojie Wang from the University of Science and Technology of China for supporting the computational sources, and also thank Prof. Yong Xiao from Zhejiang University for providing the magnetic configuration of the ITER baseline scenario. This work was supported by the National MCF Energy R &D Program of China (No. 2019YFE03060000), National Natural Science Foundation of China (Nos. 12005063, 12375215 and 12175034), and the Collaborative Innovation Program of Hefei Science Center, CAS (No. 2022HSC-CIP008).
| [1] |
ITER Organization 2018 ITER Technical Report ITR-18-003 URL https://www.iter.org/doc/www/content/com/Lists/ITER%20Technical%20Reports/Attachments/9/ITER-Research-Plan_final_ITR_FINAL-Cover_High-Res.pdf
|
| [2] |
Kritz A H et al 2011 Nucl. Fusion 51 123009 doi: 10.1088/0029-5515/51/12/123009
|
| [3] |
Kim S H et al 2016 Nucl. Fusion 56 126002 doi: 10.1088/0029-5515/56/12/126002
|
| [4] |
Meneghini O et al 2016 Phys. Plasmas 23 042507 doi: 10.1063/1.4947204
|
| [5] |
Wiesen S et al 2017 Nucl. Fusion 57 076020 doi: 10.1088/1741-4326/aa6ecc
|
| [6] |
Polevoi A R et al 2018 Nucl. Fusion 58 056020 doi: 10.1088/1741-4326/aab4ad
|
| [7] |
Na Y S et al 2019 Nucl. Fusion 59 076026 doi: 10.1088/1741-4326/ab15e0
|
| [8] |
Garzotti L et al 2019 Nucl. Fusion 59 026006 doi: 10.1088/1741-4326/aaf2f3
|
| [9] |
Asp E M et al 2022 Nucl. Fusion 62 126033 doi: 10.1088/1741-4326/ac90d4
|
| [10] |
Albergante M et al 2010 Nucl. Fusion 50 084013 doi: 10.1088/0029-5515/50/8/084013
|
| [11] |
Villard L et al 2013 Plasma Phys. Control. Fusion 55 074017 doi: 10.1088/0741-3335/55/7/074017
|
| [12] |
Garcia J, Görler T and Jenko F 2018 Phys. Plasmas 25 055902 doi: 10.1063/1.5016331
|
| [13] |
Bass E M and Waltz R E 2020 Nucl. Fusion 60 016032 doi: 10.1088/1741-4326/ab54fb
|
| [14] |
Hayward-Schneider T et al 2022 Nucl. Fusion 62 112007 doi: 10.1088/1741-4326/ac6f12
|
| [15] |
Ye L et al 2016 J. Comput. Phys. 316 180 doi: 10.1016/j.jcp.2016.03.068
|
| [16] |
Xu Y F et al 2017 Phys. Plasmas 24 082515 doi: 10.1063/1.4986395
|
| [17] |
Zhao P F, Ye L and Xiang N 2021 Comput. Phys. Commun. 269 108114 doi: 10.1016/j.cpc.2021.108114
|
| [18] |
Wang S J 2012 Phys. Plasmas 19 062504 doi: 10.1063/1.4729660
|
| [19] |
Wang S J 2013 Phys. Rev. E 87 063103 doi: 10.1103/PhysRevE.87.063103
|
| [20] |
Wang S J 2014 Phys. Plasmas 21 072312 doi: 10.1063/1.4890356
|
| [21] |
Xu Y F, Dai Z L and Wang S J 2014 Phys. Plasmas 21 042505 doi: 10.1063/1.4871726
|
| [22] |
Xiao X T et al 2017 Commun. Comput. Phys. 22 789 doi: 10.4208/cicp.OA-2016-0092
|
| [23] |
Dai Z L et al 2019 Comput. Phys. Commun. 242 72 doi: 10.1016/j.cpc.2019.04.004
|
| [24] |
Hu Y C et al 2023 Plasma Phys. Control. Fusion 65 055023 doi: 10.1088/1361-6587/acc482
|
| [25] |
Mantica P et al 2020 Plasma Phys. Control. Fusion 62 014021 doi: 10.1088/1361-6587/ab5ae1
|
| [26] |
Adam J C, Tang W M and Rutherford P H 1976 Phys. Fluids 19 561 doi: 10.1063/1.861489
|
| [27] |
Romanelli F 1989 Phys. Fluids B 1 1018 doi: 10.1063/1.859023
|
| [28] |
Dong J Q, Mahajan S M and Horton W 1997 Phys. Plasmas 4 755 doi: 10.1063/1.872169
|
| [29] |
Kim J Y and Han H S 2017 Phys. Plasmas 24 072501 doi: 10.1063/1.4990071
|
| [30] |
Lin Z et al 2007 Plasma Phys. Control. Fusion 4 9
|
| [31] |
Rewoldt G and Tang W M 1990 Phys. Fluids B 2 318 doi: 10.1063/1.859320
|
| [32] |
Coppi B and Pegoraro F 1977 Nucl. Fusion 17 969 doi: 10.1088/0029-5515/17/5/009
|
| [33] |
Dong J Q, Horton W and Kim J Y 1992 Phys. Fluids B 4 1867 doi: 10.1063/1.860040
|
| [34] |
Wang W X et al 2007 Phys. Plasmas 14 072306 doi: 10.1063/1.2750647
|
| [35] |
Chen L, Qiu Z Y and Zonca F 2024 Phys. Plasmas 31 040701 doi: 10.1063/5.0203053
|
| [36] |
Chen N F et al 2024 Phys. Plasmas 31 042307 doi: 10.1063/5.0201169
|
| [37] |
Dupree T H 1967 Phys. Fluids 10 1049 doi: 10.1063/1.1762220
|
| [38] |
Lang J Y, Parker S E and Chen Y 2008 Phys. Plasmas 15 055907 doi: 10.1063/1.2884036
|
| [39] |
Ernst D R et al 2009 Phys. Plasmas 16 055906 doi: 10.1063/1.3116282
|
| [40] |
Wang S J 2017 Phys. Plasmas 24 102508 doi: 10.1063/1.5004555
|
| [41] |
Zhang D B et al 2020 Nucl. Fusion 60 046015 doi: 10.1088/1741-4326/ab72e1
|
| [42] |
Rosenbluth M N and Hinton F L 1998 Phys. Rev. Lett. 80 724 doi: 10.1103/PhysRevLett.80.724
|
| [43] |
Wang Z H, Dai Z L and Wang S J 2022 Phys. Rev. E 106 035205
|
| [44] |
Ma Y H et al 2023 Nucl. Fusion 63 056014 doi: 10.1088/1741-4326/acc116
|
| [45] |
Diamond P H and Kim Y B 1991 Phys. Fluids B 3 1626 doi: 10.1063/1.859681
|
| [46] |
Diamond P H et al 1994 Phys. Rev. Lett. 72 2565 doi: 10.1103/PhysRevLett.72.2565
|
| [47] |
Carreras B A et al 1993 Phys. Fluids B 5 1491
|
| [48] |
Xu Y H et al 2000 Phys. Rev. Lett. 84 3867 doi: 10.1103/PhysRevLett.84.3867
|
| [1] | Lianjie MA, Debing ZHANG, Limin YU, Erbing XUE, Xianmei ZHANG, Juan HUANG, Yong XIAO, Xianzu GONG, Jinping QIAN, EAST Team. Simulation on the transition of electrostatic instabilities in EAST steady-state scenario[J]. Plasma Science and Technology, 2023, 25(5): 055103. DOI: 10.1088/2058-6272/acafc0 |
| [2] | Hongmei DU (杜洪梅), Liping ZHANG (张丽萍), Dongao LI (李东澳). THz plasma wave instability in field effect transistor with electron diffusion current density[J]. Plasma Science and Technology, 2018, 20(11): 115001. DOI: 10.1088/2058-6272/aacaef |
| [3] | Jiaqi DONG (董家齐). Kinetic micro-instabilities in the presence of impurities in toroidal magnetized plasmas[J]. Plasma Science and Technology, 2018, 20(9): 94005-094005. DOI: 10.1088/2058-6272/aad4f4 |
| [4] | Yunxiao CAO (曹云霄), Zhiqiang WANG (王志强), Jinjun WANG (王进君), Guofeng LI (李国锋). Study of talcum charging status in parallel plate electrostatic separator based on particle trajectory analysis[J]. Plasma Science and Technology, 2018, 20(5): 54019-054019. DOI: 10.1088/2058-6272/aaa195 |
| [5] | A ABBASI, M R RASHIDIAN VAZIRI. Effect of polarization force on the Jeans instability in collisional dusty plasmas[J]. Plasma Science and Technology, 2018, 20(3): 35301-035301. DOI: 10.1088/2058-6272/aa96fa |
| [6] | Congxiang LU (陆从相), Chengwu YI (依成武), Rongjie YI (依蓉婕), Shiwen LIU (刘诗雯). Analysis of the operating parameters of a vortex electrostatic precipitator[J]. Plasma Science and Technology, 2017, 19(2): 25504-025504. DOI: 10.1088/2058-6272/19/2/025504 |
| [7] | LI Dehui(李德徽), XIANG Nong(项农), LIN Yu(林郁), WANG Xueyi(汪学毅), YANG Cheng(杨程), MA Jun(马骏). Benchmark Simulations of Gyro-Kinetic Electron and Fully-Kinetic Ion Model for Lower Hybrid Waves in Linear Region[J]. Plasma Science and Technology, 2014, 16(9): 821-825. DOI: 10.1088/1009-0630/16/9/03 |
| [8] | WU Mingyu (吴明雨), LU Quanming (陆全明), ZHU Jie (朱洁), WANG Peiran (王沛然), WANG Shui (王水). Electromagnetic Particle-in-Cell Simulations of Electron Holes Formed During the Electron Two-Stream Instability[J]. Plasma Science and Technology, 2013, 15(1): 17-24. DOI: 10.1088/1009-0630/15/1/04 |
| [9] | SUN Yue (孙岳), CHEN Zhipeng (陈志鹏), WANG Zhijiang (王之江), ZHU Mengzhou (朱孟周), ZHUANG Ge (庄革), J-TEXT team. Experimental Studies of Electrostatic Fluctuations and Turbulent Transport in the Boundary of J-TEXT Tokamak Using Reciprocating Probe[J]. Plasma Science and Technology, 2012, 14(12): 1041-1047. DOI: 10.1088/1009-0630/14/12/02 |
| [10] | GAO Min (高敏), CHEN Shaoyong (陈少永), TANG Changjian (唐昌建), PENG Xiaodong (彭晓东). The electromagnetic instability in electron flow with ion background[J]. Plasma Science and Technology, 2010, 12(5): 523-528. |
| 1. | Priputnev, P.V., Romanchenko, I.V., Rostov, V.V. Systems and Technologies Based on Nonlinear Transmission Lines with Ferrite (Review). Technical Physics, 2024, 69(6): 1730-1741. DOI:10.1134/S1063784224060355 | |
| 2. | Cui, Y., Meng, J., Yuan, Y. et al. Principle analysis and preliminary experiment of the gyromagnetic nonlinear transmission lines | [旋磁非线性传输线原理分析和初步实验]. Guofang Keji Daxue Xuebao/Journal of National University of Defense Technology, 2024, 46(3): 222-228. DOI:10.11887/j.cn.202403022 | |
| 3. | Zhang, W., Lin, M., Li, H. et al. Finite element analysis of pulse sharpening effect of gyromagnetic nonlinear transmission line based on Landau-Lifshitz-Gilbert equation. Review of Scientific Instruments, 2024, 95(6): 064705. DOI:10.1063/5.0203542 | |
| 4. | Stephens, J., Wright, T., Saheb, D. et al. Experimental Characterization of a Genetic Algorithm-Optimized Nonlinear Transmission Line for High Power RF Generation. IEEE Transactions on Microwave Theory and Techniques, 2024. DOI:10.1109/TMTT.2024.3457311 | |
| 5. | Samoylichenko, M.A.. Multiple Modal Reservation in Flexible Printed Cables. 2023. DOI:10.1109/UralCon59258.2023.10291140 | |
| 6. | Jiang, J., Cao, Y., Luo, Z. et al. Simulation research on pulse steepening technology based on ferrite transmission line | [基于铁氧体传输线的脉冲陡化技术仿真研究*]. Qiangjiguang Yu Lizishu/High Power Laser and Particle Beams, 2022, 34(9): 095005. DOI:10.11884/HPLPB202234.220092 | |
| 7. | Jiang, J., Luo, Z., Cao, Y. et al. Design and Performance of a Ferrite Transmission Line Sharpener for Trigger Generator Used in FLTD. IEEE Transactions on Plasma Science, 2022, 50(9): 3113-3122. DOI:10.1109/TPS.2022.3194029 | |
| 8. | Cui, Y., Meng, J., Huang, L. et al. 100-MW-Level Experiments of a Gyromagnetic Nonlinear Transmission Line System. IEEE Transactions on Electron Devices, 2022, 69(9): 5248-5255. DOI:10.1109/TED.2022.3192215 | |
| 9. | Greco, A.F.G., Rossi, J.O., Barroso, J.J. et al. Analysis of the sharpening effect in gyromagnetic nonlinear transmission lines using the unidimensional form of the Landau-Lifshitz-Gilbert equation. Review of Scientific Instruments, 2022, 93(6): 065101. DOI:10.1063/5.0087452 | |
| 10. | Cui, Y., Meng, J., Yuan, Y. et al. Numerical Analysis on the RF Characteristics of the Gyromagnetic Nonlinear Transmission Lines. IEEE Transactions on Plasma Science, 2022, 50(5): 1188-1197. DOI:10.1109/TPS.2022.3166898 | |
| 11. | Zhu, D., Meng, J., Huang, L. et al. Simulation Research on a Compact High Power Microwave Source Based on Gyromagnetic Nonlinear Transmission Lines | [基于旋磁非线性传输线的小型化强电磁脉冲源的仿真研究]. Dianzi Yu Xinxi Xuebao/Journal of Electronics and Information Technology, 2022, 44(2): 737-744. DOI:10.11999/JEIT200912 | |
| 12. | Huang, L., Meng, J., Zhu, D. et al. Minimum Spatial Filling Rate of the Ferrite Required to Excite the Microwave Oscillations in the Gyromagnetic NLTL. IEEE Transactions on Plasma Science, 2022, 50(1): 23-28. DOI:10.1109/TPS.2021.3135022 | |
| 13. | Cui, Y., Meng, J., Huang, L. et al. Operation analysis of the wideband high-power microwave sources based on the gyromagnetic nonlinear transmission lines. Review of Scientific Instruments, 2021, 92(3): 034702. DOI:10.1063/5.0040323 | |
| 14. | Huang, L., Meng, J., Zhu, D. et al. Field-line coupling method for the simulation of gyromagnetic nonlinear transmission line based on the maxwell-LLG system. IEEE Transactions on Plasma Science, 2020, 48(11): 3847-3853. DOI:10.1109/TPS.2020.3029524 | |
| 15. | Fairbanks, A.J., Darr, A.M., Garner, A.L. A Review of Nonlinear Transmission Line System Design. IEEE Access, 2020. DOI:10.1109/ACCESS.2020.3015715 |