| Citation: | Lili DONG, Mingyuan WANG, Wenjun LIU, Yuejiang SHI, Jiaqi DONG, Dong GUO, Tiantian SUN, Xiang GU, Xianming SONG, Baoshan YUAN, Yueng-Kay Martin PENG, the ENN Team. Experimental confirmation of the linear relation between plasma current and external vertical magnetic field in EXL-50 spherical torus energetic electron plasmas[J]. Plasma Science and Technology, 2024, 26(8): 085104. DOI: 10.1088/2058-6272/ad4f23 |
A three-fluid equilibrium plasma with bulk plasma and energetic electrons has been observed on the Xuanlong-50 (EXL-50) spherical torus, where the energetic electrons play a crucial role in sustaining the plasma current and pressure. In this study, the equilibrium of a multi-fluid plasma was investigated by analyzing the relationship between the external vertical magnetic field (BV), plasma current (Ip), the poloidal ratio (βp) and the Shafranov formula. Remarkably, our research demonstrates some validity of the Shafranov formula in the presence of multi-fluid plasma in EXL-50 spherical torus. This finding holds significant importance for future reactors as it allows for differentiation between alpha particles and background plasma. The study of multi-fluid plasma provides a significant reference value for the equilibrium reconstruction of burning plasma involving alpha particles.
The primary challenge addressed in the investigation of high-temperature plasma confinement in toroidal systems is the attainment of equilibrium. In a tokamak, equilibrium is reached when the extension force is balanced by the force arising from the interplay between the plasma current (Ip) and the external vertical magnetic field (BV). In the framework of the single-fluid approximation, the required BV to sustain the equilibrium of the plasma torus is determined by the Grad-Shafranov formula [1]:
| BV=μ0Ip4πR(ln8Ra+li2−32+βp), | (1) |
where a and R are minor and major radii of the plasma column, li is the internal inductance and βp = 8π2a2⟨p⟩/μ0Ip2 is the poloidal beta. When Ip and BV are given, the position of a plasma column depends on both the kinetic energy of the plasma particles (βp) and current distribution over the column cross-section (li, R and a).
The Grad-Shafranov (G-S) equation [1–3] has been widely applied to reconstruct magnetic flux in magnetic devices [4–11] which contain a central solenoid (CS) to drive plasma current. The G-S equation is also employed in plasma non-inductive current start-up experiments utilizing RF waves [12–17] and helicity injection techniques [14, 18–21]. However, it is important to note that the G-S equation is based on the assumption of single-fluid equilibrium (\nabla{p}-\boldsymbol{J}\times \boldsymbol{B}=0 , where p is pressure) [1–3]. This raises questions about their applicability in scenarios involving burning plasma [22–24], runaway discharges [25, 26], and multi-fluid plasma with RF wave heating, specifically involving energetic electrons [16]. It remains unclear whether the G-S equation and equation (1) are suitable in such cases. To address this concern, Ishida et al derived equilibrium equations for multi-fluid systems that involving energetic particles, enabling the reconstruction of multi-fluid equilibrium [27, 28]. These equations have been subsequently applied in the EXL-50 spherical torus for magnetic flux reconstruction purposes. This paper presents the resultsof the equilibrium experiments of the EXL-50 spherical torus, which is a medium-sized spherical torus with a large number of energetic electrons carrying the main plasma current [29–31]. According to previous experiment results [30, 32–35], the energetic electrons exist and play an important role in the EXL-50 plasma, making it no longer suitable to be treated as a single-fluid plasma. Given that the simulation code based on the multi-fluid model of EXL-50 is under development, we carried an experimental investigation of the relationship between plasma current and external vertical magnetic field. We hope it can shed some light on the theoretical equilibrium model in future. The result shows that the relationship between BV, Ip and βp in EXL-50 experiments coincides with the Shafranov formula. Firstly, the relationship between Ip and BV was verified by conducting BV scans under similar plasma shape and heating conditions. Secondly, an analysis was performed on the relationship between BV/Ip and βp for nearly 500 discharges in the equilibrium state, revealing that the data predominantly followed two distinct linear trends. Further investigation confirmed that these two lines corresponded to equilibrium states with and without electron cyclotron waves (ECW), respectively. Importantly, a linear relationship between RBV/Ip and βp was observed, consistent with the Shafranov formula, while the physics model underlying still remains unclear and needs to be further investigated.
The paper is split into the following parts: the EXL-50 energetic electron contribution to the plasma current is presented in the first part, and the BV, BV/Ip, RBV/Ip and βp statistics are analyzed in the second part. The summary and discussion are in the last part.
The EXL-50 is a spherical torus without CS, with major and minor radii of approximately 0.58 m and 0.41 m, respectively, toroidal magnetic field (BT of approximately 0.5 T at r ~ 0.48 m, and aspect ratio of A > 1.45. At present, EXL-50 uses three ECW systems (28 GHz) to heat the plasma and drive the plasma current. System A (gyrotron source power of ~ 50 kW) is mainly used to produce the initial plasma and form closed flux surfaces [31], systems B and C (gyrotron source power of ~ 400 kW) are used to increase the plasma current and maintain the current flattop for multiple seconds. Discharges with plasma currents substantially above 100 kA with a 100 kW ECW are routinely obtained in EXL-50 [29], and the main current is identified as the contribution of energetic electrons [27], which are driven by stochastic ECW [36].
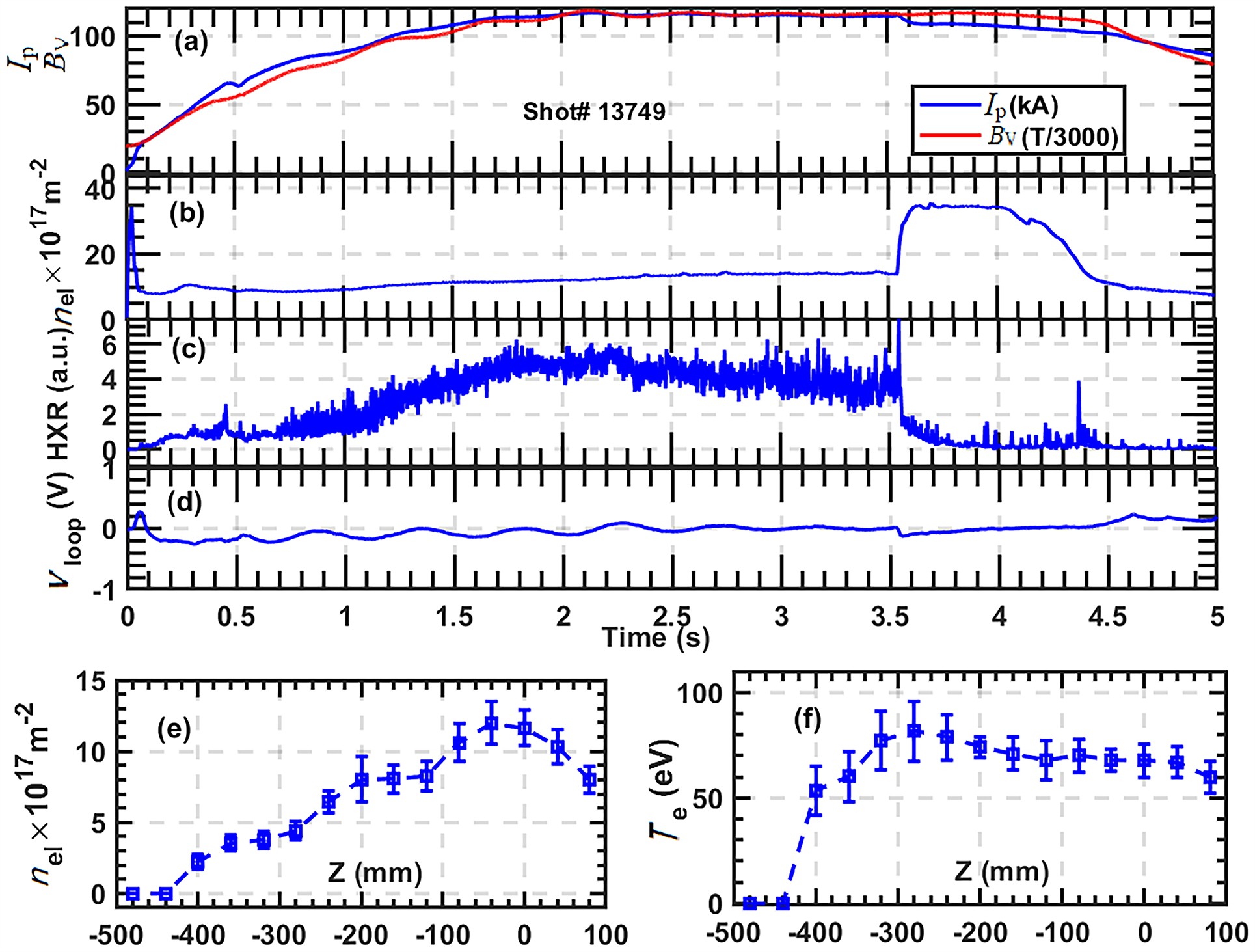
Figure 1 illustrates a typical discharge in the EXL-50 system, showcasing various plasma parameters. The sub-figures, arranged from top to bottom, depict the plasma current and BV (z ~ 0 m, R ~ 0.3 m), integral density, hard X-ray intensity [37], loop voltage and electron temperature and density profiles. The bottom two sets of profiles are electron temperature and density profiles obtained through Thomson scattering diagnostic (TS) measurements during the 2–3 s interval [38]. The ECW injected power was approximately 140 kW and was switched off after 3 s. Throughout the discharge, a consistently low loop voltage was maintained, and the plasma current remained stable at around 118 kA during the 2–3 s time period, indicating that the ECW primarily drove the plasma current. Notably, an increase in plasma current corresponds to a significant rise in hard X-ray intensity, suggesting the presence of energetic electrons in the EXL-50 system and a correlation between the plasma current and hard X-ray emission [16, 31].
The TS measurements yielded peak values of electron density and temperature at approximately 1.2×1018 m−3 and 100 eV. It is worth mentioning that since the TS beam is close to the plasma boundary, the core density and temperature may be higher. The ECW-driven current of bulk plasma was calculated using CQL3D code [39] with Te = 500 eV and ne = 1.2×1018 m−3, resulting in a current of less than 10 kA. Only when the plasma temperature reaches around 100 keV [40, 41] can a current of nearly 50 kA be driven, indicating that the plasma current is mainly carried by energetic electrons.
The EXL-50 system exhibits a significant population of energetic electrons, whose contributions to plasma current and pressure cannot be disregarded [12, 17, 27]. Consequently, the conventional single-fluid assumption of the G-S equation does not hold for the EXL-50 plasma. Indeed the EFIT equilibrium construction, which assumes G-S single-fluid MHD equilibrium and the plasma current only inside the last closed flux surface (LCFS), does not fit the EXL-50 experiments well. Therefore, experiments were conducted to investigate the multi-fluid equilibrium in the system.
The linear relationship between BV and Ip has been extensively established in steady-state tokamak plasma [12–17, 19, 42, 43]. In this study, the relationship between Ip and BV in a multi-fluid steady-state plasma on EXL-50 was investigated. By progressively increasing BV on a shot-by-shot basis, while maintaining a constant injection power ECW at 20 kW and 130 kW, we examined the correlation between BV and Ip. Figure 2 illustrates that Ip exhibited a linear and positive relationship with BV under similar heating conditions and plasma shapes, in agreement with the Shafranov formula.
To further investigate the validity of the Shafranov formula in a multi-fluid plasma scenario, we conducted an analysis of the relationship between the ratio BV/Ip and βp in approximately 500 steady-state plasma discharges. Diamagnetic measurement, a widely employed technique in fusion devices [44–46], was utilized to derive the poloidal beta, βp from the toroidal magnetic flux produced by the plasma, and using the equilibrium relation, given here in its simplified form:
| {\beta }_{\mathrm{p}}=1-\frac{8{\text{π}}{B}_{\mathrm{T}}}{{\mathrm{\mu }}_{0}{I}_{\mathrm{p}}^{2}} {\text{Δ}} \varphi , | (2) |
where ∆φ is the diamagnetic flux.
In figure 3, the horizontal axis is βp (equation (2)), the vertical axis is BV/Ip and the intensity corresponds to the number of occurrences. Notably, two distinct bright regions are observed within the figure, each displaying a linear relationship between BV/Ip and βp along a specific line (referred to as line 1 and line 2). Six points (pentagons, a–f markers) are randomly selected from the figure to investigate the causes of the bright regions.
Figure 4 presents visible light plasma images corresponding to the pentagon marked data in figure 3. The images were used to determine the brightness boundary and estimate the large and small radii of the plasma using a simple fitting calculation (indicated by the green dashed line). It should be noted that cases (a) and (b) represent scenarios where the ECW was turned off, and the effect of hard X-rays on the camera was negligible.
Observing the plasma images, it is evident that the βp increases significantly in line 1 and line 2, while the plasma shape in the CCD camera remains unchanged from figures 4(a) and (b) and from figures 4(c) and (d). Moreover, the plasma region varies considerably at similar βp ((a), (c), (d) and (b), (e), (f)), which suggests that the two-line region in figure 3 may be affected by the R variation of the plasma.
The relationship between 4πBVR/μ0Ip and βp is shown in figure 5. The βp is approximately linear with 4πBVR/μ0Ip, which agrees with the Shafranov formula.
Equilibrium is a crucial aspect of tokamak devices, particularly for future magnetic confinement devices, where achieving fusion plasma necessitates the use of strong neutral beam injection (NBI) and microwave heating, as well as the presence of a large number of energetic alpha particles generated during fusion [47–50]. This indicates that the application of conventional single-fluid G-S equilibrium to combustion plasma equilibrium reconstruction [51] cannot be confidently relied upon.
In the above demonstration, we conducted multi-fluid equilibrium magnetic surface reconstruction and statistical analysis of equilibrium parameters on the EXL-50 device, yielding preliminary results. Firstly, the linear relationship between BV and Ip was experimentally confirmed for similar discharge conditions. Secondly, statistical analysis found that there is also a linear relationship between BV/Ip and βp. Finally, the relationship between 4πBVR/μ0Ip and βp under different plasma shapes was estimated using the CCD camera, revealing a positive correlation between 4πBVR/µ0Ip and βp, in agreement with the Shafranov formula.
Though the experimental result of EXL-50 generally fits the G-S equation, there are still problems remaining unsolved on EXL-50 spherical torus. Despite the fact that multi-fluid plasma, which includes energetic particles, does not meet the assumption of single-fluid equilibrium, the Shafranov formula still exhibits some applicability. This finding holds significance for the control of plasma shape in fusion plasma and runaway discharge. However, it should be noted that the present study represents an initial phase in the pursuit of combustion plasma control and equilibrium reconstruction, and there is still much ground to cover in this field.
| [1] |
Shafranov V D Plasma equilibrium in a magnetic held In: Leontovich M A Reviews of Plasma Physics New York: Consultants Bureau 1966
|
| [2] |
Swain D W and Neilson G H 1982 Nucl. Fusion 22 1015 doi: 10.1088/0029-5515/22/8/002
|
| [3] |
Shafranov V D 1971 Plasma Phys. 13 757 doi: 10.1088/0032-1028/13/9/006
|
| [4] |
Ferron J R et al 1998 Nucl. Fusion 38 1055 doi: 10.1088/0029-5515/38/7/308
|
| [5] |
Lao L L et al 2005 Fusion Sci. Technol. 48 968 doi: 10.13182/FST48-968
|
| [6] |
Lao L L et al 1990 Nucl. Fusion 30 1035 doi: 10.1088/0029-5515/30/6/006
|
| [7] |
Dory R A and Peng Y K M 1977 Nucl. Fusion 17 21 doi: 10.1088/0029-5515/17/1/003
|
| [8] |
Hofmann F and Tonetti G 1988 Nucl. Fusion 28 1871 doi: 10.1088/0029-5515/28/10/014
|
| [9] |
Feneberg W and Lackner K 1973 Nucl. Fusion 13 549 doi: 10.1088/0029-5515/13/4/008
|
| [10] |
Turnbull A D et al 1998 Nucl. Fusion 38 1467 doi: 10.1088/0029-5515/38/10/305
|
| [11] |
Zheng S B, Wootton A J and Solano E R 1996 Phys. Plasmas 3 1176 doi: 10.1063/1.871772
|
| [12] |
Maekawa T et al 2005 Nucl. Fusion 45 1439 doi: 10.1088/0029-5515/45/11/026
|
| [13] |
Kubo S et al 1983 Phys. Rev. Lett. 50 1994 doi: 10.1103/PhysRevLett.50.1994
|
| [14] |
Zheng S B et al 2000 Nucl. Fusion 40 155 doi: 10.1088/0029-5515/40/2/301
|
| [15] |
Uchida M et al 2010 Phys. Rev. Lett. 104 065001 doi: 10.1103/PhysRevLett.104.065001
|
| [16] |
Tashima S et al 2014 Nucl. Fusion 54 023010 doi: 10.1088/0029-5515/54/2/023010
|
| [17] |
Yoshinaga T et al 2006 Phys. Rev. Lett. 96 125005 doi: 10.1103/PhysRevLett.96.125005
|
| [18] |
Battaglia D J et al 2009 Phys. Rev. Lett. 102 225003 doi: 10.1103/PhysRevLett.102.225003
|
| [19] |
Ono M et al 1987 Phys. Rev. Lett. 59 2165 doi: 10.1103/PhysRevLett.59.2165
|
| [20] |
Battaglia D J et al 2011 Nucl. Fusion 51 073029 doi: 10.1088/0029-5515/51/7/073029
|
| [21] |
Raman R et al 2006 Phys. Rev. Lett. 97 175002 doi: 10.1103/PhysRevLett.97.175002
|
| [22] |
Thomas P R et al 1998 Phys. Rev. Lett. 80 5548 doi: 10.1103/PhysRevLett.80.5548
|
| [23] |
JET Team 1999 Nucl. Fusion 39 1619 doi: 10.1088/0029-5515/39/11Y/301
|
| [24] |
Nocente M et al 2017 Nucl. Fusion 57 076016 doi: 10.1088/1741-4326/aa6f7d
|
| [25] |
Eriksson L G and Helander P 2003 Comput. Phys. Commun. 154 175 doi: 10.1016/S0010-4655(03)00293-5
|
| [26] |
Harvey R W et al 2000 Phys. Plasmas 7 4590 doi: 10.1063/1.1312816
|
| [27] |
Ishida A, Peng Y K M and Liu W J 2021 Phys. Plasmas 28 032503 doi: 10.1063/5.0027718
|
| [28] |
Ishida A et al 2015 Plasma Fusion Res. 10 1403084 doi: 10.1585/pfr.10.1403084
|
| [29] |
Shi Y J et al 2022 Nucl. Fusion 62 086047 doi: 10.1088/1741-4326/ac71b6
|
| [30] |
Guo D et al 2022 Plasma Phys. Control. Fusion 64 055009 doi: 10.1088/1361-6587/ac5a08
|
| [31] |
Wang M Y et al 2022 Plasma Phys. Control. Fusion 64 075006 doi: 10.1088/1361-6587/ac70fb
|
| [32] |
Wang M Y et al 2023 J. Plasma Phys. 89 905890603 doi: 10.1017/S0022377823001216
|
| [33] |
Wang M Y et al 2023 Nucl. Fusion 63 076024 doi: 10.1088/1741-4326/acd4d2
|
| [34] |
Wang M Y et al 2023 Plasma Sci. Technol. 25 045104 doi: 10.1088/2058-6272/aca373
|
| [35] |
Wang M Y et al 2024 Phys. Plasmas 31 032105 doi: 10.1063/5.0195750
|
| [36] |
Ikegami H et al 1973 Nucl. Fusion 13 351 doi: 10.1088/0029-5515/13/3/005
|
| [37] |
Cheng S K et al 2021 Rev. Sci. Instrum. 92 043513 doi: 10.1063/5.0040636
|
| [38] |
Li H Y et al 2022 Rev. Sci. Instrum. 93 053504 doi: 10.1063/5.0088785
|
| [39] |
Harvey R W and McCoy M G The cql3d fokker-planck code. In Proceedings of the IAEA Technical Committee Meeting on Simulation and Modeling of Thermonuclear Plasmas (pp. 489–526) 1992
|
| [40] |
Petrov Y V and Harvey R W 2016 Plasma Phys. Control. Fusion 58 115001 doi: 10.1088/0741-3335/58/11/115001
|
| [41] |
Petrov Y V, Parks P B and Harvey R W 2021 Plasma Phys. Control. Fusion 63 035026 doi: 10.1088/1361-6587/abdacc
|
| [42] |
Takase Y et al 2013 Nucl. Fusion 53 063006 doi: 10.1088/0029-5515/53/6/063006
|
| [43] |
Jones I R 1999 Phys. Plasmas 6 1950 doi: 10.1063/1.873452
|
| [44] |
Moret J M, Buhlmann F and Tonetti G 2003 Rev. Sci. Instrum. 74 4634 doi: 10.1063/1.1614856
|
| [45] |
Tonetti G, Christiansen J P and de Kock L 1986 Rev. Sci. Instrum. 57 2087 doi: 10.1063/1.1138747
|
| [46] |
Lazzaro E and Mantica P 1988 Plasma Phys. Control. Fusion 30 1735 doi: 10.1088/0741-3335/30/12/008
|
| [47] |
Pinches S D et al 2015 Phys. Plasmas 22 021807 doi: 10.1063/1.4908551
|
| [48] |
Uckan N A et al 1988 Fusion Technol. 13 411 doi: 10.13182/FST88-A25117
|
| [49] |
Sharapov S E et al 2008 Fusion Sci. Technol. 53 989 doi: 10.13182/FST08-A1745
|
| [50] |
Heidbrink W W and White R B 2020 Phys. Plasmas 27 030901 doi: 10.1063/1.5136237
|
| [51] |
Ishida A and Steinhauer L C 2012 Phys. Plasmas 19 102512 doi: 10.1063/1.4762846
|
| [1] | Hanyu ZHANG, Lina ZHOU, Yueqiang LIU, Guangzhou HAO, Shuo WANG, Xu YANG, Yutian MIAO, Ping DUAN, Long CHEN. Deep learning approaches to recover the plasma current density profile from the safety factor based on Grad–Shafranov solutions across multiple tokamaks[J]. Plasma Science and Technology, 2024, 26(5): 055101. DOI: 10.1088/2058-6272/ad13e3 |
| [2] | Yifeng FU (傅一峰), Cheng ZHOU (周成), Peng WU (吴鹏), Zhongkai ZHANG (张仲恺), Zun ZHANG (张尊), Haibin TANG (汤海滨). A plasma equilibrium model for rapid estimation of SF-MPDT performance[J]. Plasma Science and Technology, 2021, 23(10): 104005. DOI: 10.1088/2058-6272/ac199e |
| [3] | Bin WU (武斌), Chao GAO (高超), Feng LIU (刘峰), Ming XUE (薛明), Yushuai WANG (王玉帅), Borui ZHENG (郑博睿). Reduction of turbulent boundary layer drag through dielectric-barrier-discharge plasma actuation based on the Spalding formula[J]. Plasma Science and Technology, 2019, 21(4): 45501-045501. DOI: 10.1088/2058-6272/aaf2e2 |
| [4] | Kai ZHAO (赵凯), Baigang SUN (孙佰刚), Yongji LU (卢永吉), Feng LI (李锋), Yongbo LIU (刘永波), Xiangbin LIU (刘祥彬), Kefu WANG (王可夫). Experimental investigation on plasma jet deflection with magnetic fluid control based on PIV measurement[J]. Plasma Science and Technology, 2019, 21(2): 25503-025503. DOI: 10.1088/2058-6272/aae09b |
| [5] | Yinan WANG (王一男), Shuaixing LI (李帅星), Li WANG (王莉), Ying JIN (金莹), Yanhua ZHANG (张艳华), Yue LIU (刘悦). Effects of HF frequency on plasma characteristics in dual-frequency helium discharge at atmospheric pressure by fluid modeling[J]. Plasma Science and Technology, 2018, 20(11): 115402. DOI: 10.1088/2058-6272/aac71e |
| [6] | M S CHU (朱名盛), Yemin HU (胡业民), Wenfeng GUO (郭文峰). Generalization of Solovev’s approach to finding equilibrium solutions for axisymmetric plasmas with flow[J]. Plasma Science and Technology, 2018, 20(3): 35101-035101. DOI: 10.1088/2058-6272/aa9841 |
| [7] | Xiang HE (何湘), Chong LIU (刘冲), Yachun ZHANG (张亚春), Jianping CHEN (陈建平), Yudong CHEN (陈玉东), Xiaojun ZENG (曾小军), Bingyan CHEN (陈秉岩), Jiaxin PANG (庞佳鑫), Yibing WANG (王一兵). Diagnostic of capacitively coupled radio frequency plasma from electrical discharge characteristics: comparison with optical emission spectroscopy and fluid model simulation[J]. Plasma Science and Technology, 2018, 20(2): 24005-024005. DOI: 10.1088/2058-6272/aa9a31 |
| [8] | Hailong GAO (高海龙), Tao XU (徐涛), Zhongyong CHEN (陈忠勇), Ge ZHUANG (庄革). Plasma equilibrium calculation in J-TEXT tokamak[J]. Plasma Science and Technology, 2017, 19(11): 115101. DOI: 10.1088/2058-6272/aa7f26 |
| [9] | LUO Bing (罗兵), LUO Zhengping (罗正平), XIAO Bingjia (肖炳甲), YOU Wei (尤玮), TAN Mingsheng (谭名昇), GUO Yong (郭勇), BAI Wei (白伟), MAO Wenzhe (毛文哲), LI Hong (李弘), LIU Adi (刘阿娣), LAN Tao (兰涛), XIE Jinlin (谢锦林), LIU Wandong (刘万东). Capability Assessment of the Equilibrium Field System in KTX[J]. Plasma Science and Technology, 2016, 18(1): 90-96. DOI: 10.1088/1009-0630/18/1/16 |
| [10] | M. ANWARI, H. H. QAZI, SUKARSAN, N. HARADA. Numerical Analysis of MHD Accelerator with Non-Equilibrium Air Plasma[J]. Plasma Science and Technology, 2012, 14(12): 1110-1115. DOI: 10.1088/1009-0630/14/12/14 |