| Citation: | Rui TAN, Guanrong HANG, Pingyang WANG. Optimization of magnetic field design for Hall thrusters based on a genetic algorithm[J]. Plasma Science and Technology, 2024, 26(7): 075503. DOI: 10.1088/2058-6272/ad3286 |
Magnetic field design is essential for the operation of Hall thrusters. This study focuses on utilizing a genetic algorithm to optimize the magnetic field configuration of SPT70. A 2D hybrid PIC-DSMC and channel-wall erosion model are employed to analyze the plume divergence angle and wall erosion rate, while a Farady probe measurement and laser profilometry system are set up to verify the simulation results. The results demonstrate that the genetic algorithm contributes to reducing the divergence angle of the thruster plumes and alleviating the impact of high-energy particles on the discharge channel wall, reducing the erosion by 5.5% and 2.7%, respectively. Further analysis indicates that the change from a divergent magnetic field to a convergent magnetic field, combined with the upstream shift of the ionization region, contributes to the improving the operation of the Hall thruster.
Hall thrusters are effective electric propulsion systems that are presently employed for various applications, including satellite-orbit-attitude adjustment and deep space exploration [1, 2]. Next-generation Hall thrusters will be designed to meet the requirements of increased specific impulse, thrust and life expectancy [3, 4].
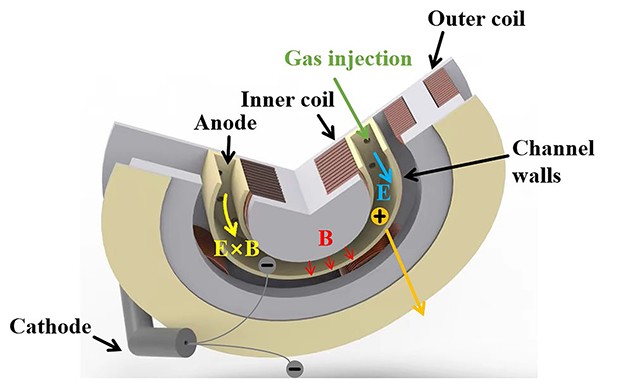
The specific impulse of a Hall thruster can range from 1000 to 3000 s [5]. Xenon is frequently used as the working fluid in Hall thrusters due to its advantageous properties, including high molecular weight, low ionization energy, and high chemical stability [6, 7]. Xenon gas is ionized in the discharge channel after being injected from the anode. The anode is situated at the upstream end of the discharge channel and is surrounded by concentric walls that enclose the channel both internally and externally, as shown in figure 1.
Either an array of solenoids or permanent magnets can produce a radial magnetic field, with maximum strength occurring near the exhaust of the channel. The magnetic field configuration is essential for the overall functioning of the Hall thruster [8, 9]. It plays a role in confining the electron movement from the cathode to the anode, facilitating the formation of Hall current in the discharge channel. This Hall current increases the probability of collision with xenon atoms and the overall ionization efficiency. Notably, the ion trajectories should not be disturbed by the magnetic field. Meanwhile, the primary generation of an axial electric field occurs predominantly at the channel’s exit because of electron resistivity. This electric field accelerates the ionized xenon gas and propels it out, creating thrust and specific impulse [10, 11]. Some of the electrons supplied by the cathode neutralize the plume, thereby preventing it from impacting the spacecraft’s surface and interfering with its normal operation [12].
The magnetic field has a vital part in shaping and stabilizing the thruster plume [13]. An efficacious magnetic field topology can exert substantial control over ionization oscillatory issues within the thruster [14‒18] because it substantially influences the ionization and acceleration processes [19, 20]. Furthermore, the topology can reduce the influence of high-energy particles on the discharge channel’s walls, extending the thruster’s lifespan [3, 21‒23]. Therefore, a well-designed magnetic field structure can optimize the thruster’s performance and improve its efficiency [1, 24, 25].
Accordingly, extensive experimental and numerical studies have been conducted on magnetic field designs. For example, Hofer and Gallimore conducted research on a 5 kW-class Nasa-173M v2 Hall thruster [26]. The thruster featured two sets of solenoid coils, inside and outside. In addition, it had two trim coils for magnetic field configuration adjustment and thruster-performance improvement. However, the characteristic parameters of the magnetic field topology were interconnected. Since it is impossible to change only one of the elements while maintaining the others, it is extremely difficult to conduct a comprehensive examination of the magnetic field configuration. Garrigue et al performed numerical simulations on four types of magnetic field configurations for the SPT Hall thruster and discovered that the zero magnetic field configuration can increase the thruster’s efficiency and reduce wall corrosion [27]. To improve the flexibility of magnetic field designs, Mazouffre et al designed a variable-field configuration thruster, namely PPS-Flex, and verified the feasibility of the magnetic field design through simulations [28]. However, most recent studies are centered around showcasing the benefits of magnetic fields that already exist through numerical simulations and experiments. The design of magnetic fields frequently requires inherited experience and iterative optimization based on experimental results. However, the application of algorithmic calculations to optimize magnetic field configurations has remained a largely unexplored domain.
The complexity of magnetic field design is determined by the correlation between its characteristic parameters and the highly nonlinear characteristics. Genetic algorithms can select the best individuals from extremely complex sample groups for optimization iteration, thereby affording approximate optimal solutions [29, 30]. In this study, we employ a genetic algorithm to optimize the magnetic field configuration of SPT70, a thruster modified from SPT100 and suitable for low-power operations [31, 32]. The magnetic field configuration is considered as a characteristic of the Hall thruster population for natural selection. Using this algorithm, the magnetic field configuration is continuously optimized to minimize the angle of divergence, enhance the overall effectiveness of the thruster, and reduce the influence of high-energy particles on the discharge channel. Section 2 presents the utilized computational model and the parameter settings of the genetic algorithm. In section 3, the experimental apparatus and setup of SPT70 are presented. In section 4, the optimization results of the genetic algorithm are examined and contrasted with the experimental findings for accuracy verification. The last section provides a summary of the findings and addresses the limitations of the study.
This study utilizes machine learning to enhance the design of magnetic fields to strengthen the functionality of Hall thrusters. The discharge channel and the area around the plume are the focal points of this study, where the ionizing and accelerating characteristics of xenon gas are analyzed to examine the operational features of the thrusters under varying magnetic field characteristics. The magnetic field is generated by the inner coil, outer coil, and internal trim coil, which is adjustable by tuning the excitation current in each coil. The simulation area is shown in figure 2.
The simulation employs a hybrid two-dimensional PIC-DSMC model, where the heavy particles are directly tracked and electrons are treated as continuous fluids because of their high response speed compared to those of ions. The electric potential is calculated using Bolzmann’s equation [10, 33]. The electric potential, V, is the total of reference electric potential, Vr, and another term correlated with the electron temperature, Te, and the electron density n:
| V=Vr+KBTeeln(nn0), | (1) |
where KB is the Boltzmann’s constant and n0 is the reference density of electrons.
During the operation of the SPT, charged particles are subjected to electromagnetic fields, wherein they collide with other particles. Additionally, they are likely to hit the wall of the acceleration channel, resulting in phenomena, such as wall sheath, wall sputtering, and energy deposition [34]. The collision model employed in this study considers neutral particles, electrons, and positive ions interacting with the wall.
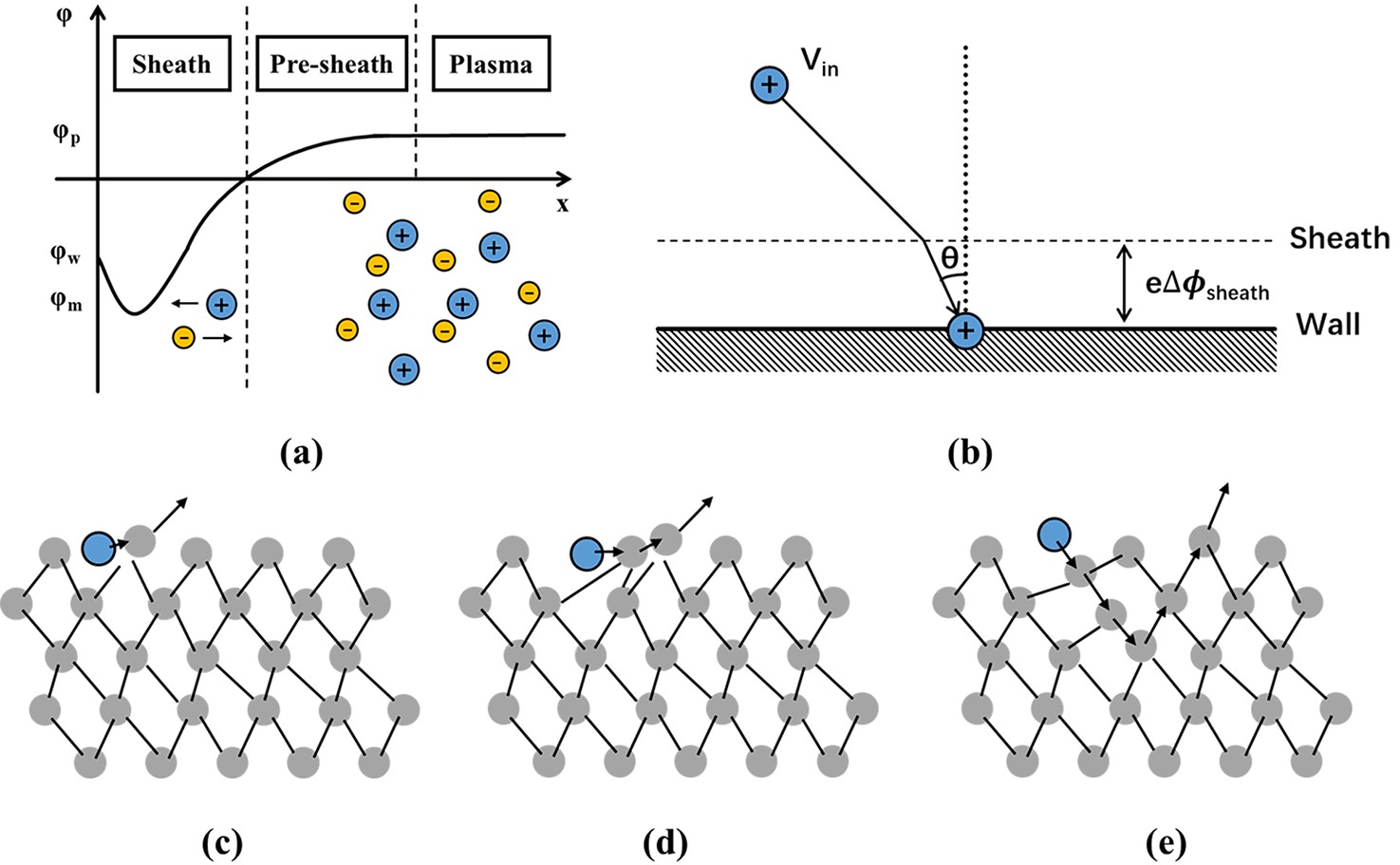
The sheath layer is located between the plasma cluster and the solid wall, as shown in figure 3(a). Its thickness is approximately equal to the Debye length [35]. This region is not electrically neutral; thus, the quasi-electric neutrality assumption cannot be applied. When the plasma collides with the wall, the electron current density flowing towards the wall is considerably greater than the ion-current density, resulting in a negative potential in this region [36]. This negative potential impedes the flow of electrons and accelerates ion flow, ultimately achieving particle-flow equilibrium. The wall potential is determined by [37]:
| ϕw=−Teeln(mi2πme)12. | (2) |
The erosion and removal of the wall material significantly affect the thruster’s performance. The complete removal of the ceramic material will completely expose the magnetic circuit to the plasma, effectively ending the life of the thruster [38, 39]. Sputtering is a common occurrence in plasma-material interactions. This is because the plasmas in Hall thrusters comprise particles with sufficient energy to break the bonds between atoms on a material’s surface. These particles can be neutral particles, ions, or electrons.
Figure 3 shows three ion-bombardment mechanisms through which target atoms are produced. Figure 3(c) shows that the incident ion directly bombards the surface of the material and directly displaces the target atoms that collide with it. Figure 3(d) shows that after the impacted target atom absorbs energy, it collides with adjacent atoms and shoots them out. As shown in figure 3(e), the incident ions induce cascade collisions on the target material, and the surface target atoms are ejected through secondary collisions. Clearly, the mechanism through which target atoms are ejected from the surface of the target depends on a series of factors, such as the type of incident ion, incident ion energy, incident angle, crystal structure of the target surface, target surface binding energy, and target surface morphology. Considering that the actual sputtering process of these factors is highly complex, and that the three sputtering mechanisms mentioned above may occur simultaneously, the net effect caused by the sputtering process is described using the sputtering yield.
Ions reached the wall at a certain angle and energy, carrying the ion kinetic energy and the sheath potential energy. The schematic diagram of the ion bombardment on the ceramic surface is shown in figure 3(b).
| Ei=12miV2in+eΔϕsheath, | (3) |
where Vin is the ion velocity, and eΔϕsheath is the potential energy in sheath. The ions acquire kinetic energy in the sheath, and the increase in their normal velocity is given by
| ΔVin=√eΔϕsheathmi. | (4) |
The angle of ion bombardment on the ceramic wall is expressed as follows:
| θ=tan−1(VtVn+ΔVn), | (5) |
where Vn and Vt are the combined normal and tangential velocities of the ion before it enters the sheath. The acceleration effect of the sheath reduces the ion-bombardment angle.
The yield from sputtering is influenced by factors such as the energy and angle of ion incidence, the nature of the target, and the temperature of the target material. High-temperature targets are more prone to sputtering. The relationship between the sputtering yield of BN-SiO2 and the temperature has been studied by Reinke et al [40, 41]. The study showed that the sputtering yield increases substantially when the ion’s impacting energy surpasses 600 °C, whereas the change in the sputtering yield is not significant below 600 °C. During steady-state plasma operation, the maximum temperature on the wall is within 500 °C. Therefore, the sputtering yield investigated in this work does not consider changes related to the target temperature. SPT70 uses BN-SiO2 as the discharge channel wall material, and the relationship is shown in the figures 4 and 5.
| Y(θ)Y(0)=cos−fθexp[−(fcosθopt(cos−1θ−1))]. | (6) |
θopt is the ion incidence angle generated by the maximum sputtering amount, and f is a parameter related to the material. The values of θopt and f are 75° and 3.2, respectively.
In this section, we introduce the key steps in the genetic algorithm, including coding, crossover, mutation, and selection. The complete process of the genetic algorithm is shown in figure 6.
The genetic algorithm selects individual traits by imitating natural selection processes. In the course of this research, the individual traits are the different magnetic field topologies of the SPT70 Hall thruster. Since the geometric structure and materials of the Hall thruster itself are fixed based on the adoption of a fixed prototype, the configuration of the magnetic field is entirely governed by the three excitation currents inside the inner coil, outer coil, and trim coil.
The intensity of the excitation current in each coil is encoded sequentially using binary code. For this calculation, 24 bits are assigned to each variable, resulting in a total string length of 72 bits. The accuracy of the calculation results depends on the encoding length [42]. With 24 bits for each current, we can obtain a solution accuracy of 0.12‒0.28 mA in the interval (0, Imax):
| (xui−xli)10α⩽ | (7) |
where x_i^{\text{u}} is the upper limit of variable x_i^{} , x_i^{\text{l}} is the lower limit of variable x_i^{} , \alpha is the precision of the variable, and \beta is the encoding string length.
Typically, the fitness function is applied to each individual to evaluate its quality. The fitness function measures how well the individual solves the problem and assigns a fitness score to the individual. The genetic algorithm is naturally suitable for solving maximization problems. However, in this study, the magnetic field that results in small divergence angles is more likely to survive. For minimization problems, the transition from the natural objective function to the fitness function was implemented as follows [29, 43]:
| F\left( x \right) = \frac{1}{{1 + f\left( x \right)}} , | (8) |
where f\left( x \right) is the objective function, representing the divergence angle of the thruster plume, and F\left( x \right) is the fitness function.
The selection process bears a resemblance to the mechanism of natural selection. Individuals with relatively small divergence angles have a high chance of being selected for reproduction. In this study, the roulette-wheel selection algorithm is employed [29]. The algorithm works by assigning a probability to each individual based on their fitness score. The roulette-wheel selection algorithm is a simple yet effective method of ensuring that the most well-adapted individuals are chosen for subsequent generations (see figure 7).
Crossover is the process of exchanging genetic material among two progenitor individuals for the generation of new progeny. This procedure helps to combine the best features of the parents and generate new solutions that may be better than the original ones. Mutation, conversely, is the process of randomly changing the genetic material of an individual to explore new solutions that may not be present in the population. This process helps to maintain the diversity of the population and avoid premature convergence.
Crossover and mutation processes are crucial for the success of the genetic algorithm. Crossover helps to explore the search space efficiently and generate high-quality solutions. Mutation helps to maintain the diversity of the population and avoid stagnation in the local optima. Therefore, maintaining a proper equilibrium of crossover and mutation rates is essential for the genetic algorithm to deliver the best performance. In this study, the crossover and mutation probabilities are assigned values of 0.3 and 0.015, respectively.
Notably, determining the optimal population size in genetic algorithms is a crucial for achieving the best possible results. The population size should be sufficiently large to ensure that the algorithm explores a wide range of solutions, but not so large that the computational cost increases. The population size is assigned a value of 200 in this study.
Each thruster entity is digitally archived on the hard disk, encapsulating a suite of input files that include the thruster dimensions, magnetic field configurations, grid information, and the sputter yield fitting results. The genetic algorithm orchestrates a sequential computation workflow, which begins with ionization calculations for each entity. The computation results are loaded into memory to facilitate the generation of offspring. The progeny data are then returned to the hard disk storage. This iterative process continues, cycling through the generations, until the genetic algorithm converges to a satisfactory solution, as illustrated in figure 8.
All experiments were carried out in the Vacuum Chamber at the Advanced Space Propulsion Laboratory jointly built by the Shanghai Jiao Tong University and the Shanghai Institute of Space Propulsion. A diagram illustrating the layout of the facility and experimental arrangement is depicted in figure 9(a).
The stainless-steel chamber has dimensions of 3 m in length and 1.5 m in diameter. The vacuum setup includes three vane rotary pumps, a Roots pump, and a pair of oil diffusion pumps. The vane rotary pump and the Roots pump as the fore pumps have the pumping speeds of 80 L/s and 600 L/s, respectively. Oil-diffusion pumps, having a com-bined pumping capacity of 33000 L/s, serve a significant function in the vacuum performance of the chamber. The chamber pressure is overseen by a resistance gauge and an ionization gauge for low and high vacuum pressures, respectively. The lowest achievable vacuum pressure can attain 3 × 10−5 Pa. When all pumps are operational, a baseline pressure as minimal as 2 × 10−4 Pa is maintained, and the pressure is sustained below 1.2×10−2 Pa under a total xenon flow of 10 sccm.
The prototype of the SPT70 employed in our experiments, along with its storage and supply system, is presented in figure 10. The standard operational performance characteristics of the SPT70 are outlined in table 1.
| Thruster type | Mass flow rate (mg/s) |
Rated power (W) |
Voltage (V) | Thrust (mN) | Specific impulse (s) |
| SPT70 | 2.6 | 650 | 300 | 40 | 1510 |
The angle of divergence serves as a critical metric for the operational efficiency of Hall thrusters. The calculation formula is as follows [44]:
| 0.95{I_{\text{b}}} = 2{\text{π}r^2}\int_{0}^{{{\theta _{{\text{div}}}}}} {j\left( \theta \right)} \sin \left( \theta \right){\text{d}}\theta , | (9) |
where
| {I_{\text{b}}} = 2{\text{π}r^2}\int_{0}^{\tfrac{{\text{π}} }{2}} {j\left( \theta \right)} \sin \left( \theta \right){\text{d}}\theta . | (10) |
The Faraday probe employed during the experimental trials represents a guard-ring-type probe. The diameter of the collector is 10 mm, and there exists a 0.2 mm space between the collector and the protective ring. A photograph of the probe as well as the circuit is displayed in figure 9(b).
In the context of the Hall Effect Thruster (HET) plume’s sheath, the gap’s distance aligns with the sheath thickness, safeguarding the collector from off-axis plasma. The collector and guard ring maintain a negative bias of −20 V to deter electron interference. By analyzing the ion current collected, we deduce the local current density within the plume and the plume’s divergence angle under specific experimental parameters [45], as depicted in figure 9(c).
In the conducted experiment, the wall surface corrosion of the Hall Thruster’s discharge channel was assessed using a laser profilometry system, namely Taylor Hobson i120 provided by Shanghai Institute of Space Propulsion. This apparatus encompasses a laser source, a detector, and a computer for data analysis, as depicted in figure 9(d). The laser beam is projected towards the thruster wall, with the detector capturing the reflected light. The subsequent data is analyzed by the computer, generating a comprehensive erosion profile. The laser, detector, and thruster are securely fixed on an optically pure aluminum structure. The thruster is attached to a rotatory stage, while the laser is manipulated to intersect the thruster’s center with its light plane. Typically, erosion profiles for both the inner and outer walls of the discharge channel are plotted at intervals of 1°. The average deviation in radial and axial directions is less than 0.06 mm, determined by inspecting width of distortion from the captured beam profiles of the profiles of erosion reported in this research.
In accordance with the calculation outcomes of the divergence angle of the thruster plume, the genetic algorithm experiences 200 generations in total before achieving convergence. During the iteration process, the divergence angle reduces significantly (see figure 11). The magnetic field configuration and the ion-density distribution of the best individuals in the 5th, 50th, and 150th generations are shown in figure 12.
The calculation results of the genetic algorithm show that, at first, the genetic algorithm mainly aims to stabilize the plasma clusters in the ionization and plume regions. At this stage, the plasma densities of the plume fluctuate significantly. Further, the excitation current intensity in coils is continuously increasing. This suggests that the magnetic field with the highest level of strength at the exit of the discharge channel has yet to be created. Consequently, electrons are not completely bound and are unable to undergo effective rotational motion to generate Hall current. Therefore, at this stage, the ionization rate is relatively low, the number density of ion clusters is low, and many atoms leave the discharge channel without undergoing ionization. The algorithm mainly increases the magnetic field intensity by increasing the excitation current of the inner and outer coils. However, in this process, the current of the internal trim coil fluctuates significantly, showing some irregular characteristics.
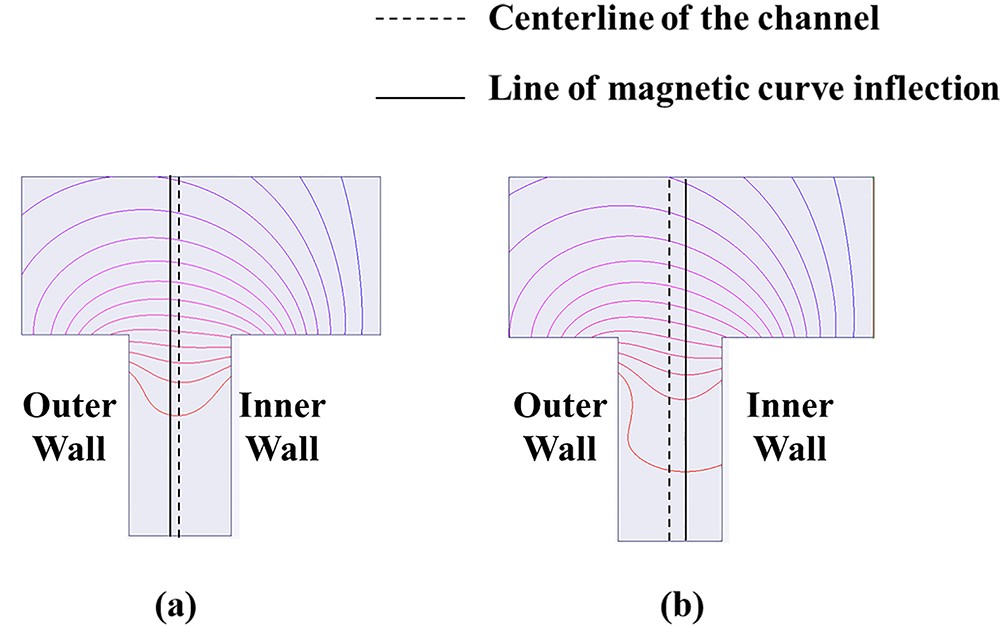
From the 50th generation of thrusters to the 150th generation of thrusters, the genetic algorithms adjust the current intensity in the internal and external excitation coils to shift the turning point of the magnetic field line inward, thereby, gradually moving from the outer side of the channel centerline to the inner side of the channel centerline. This causes the magnetic field shape to change from a divergent magnetic field to a convergent magnetic field, as shown in figures 13 and 14. It is believed that this shift of the magnetic curve inflection causes a reduction in the plume’s angle of divergence during the iteration period [46].
From the 100th generation to the 150th generation, the intensities of the current of the inner and outer excitation coils gradually achieved stability. From this point, the excitation current inside the trim coil gradually began to stabilize. Since the magnetic field shape is already shifted to a convergent configuration at this time, it is believed that the genetic algorithm further searches for better magnetic field topology by fine-tuning the excitation current in the trim coil.
From another perspective, the point with the highest magnetic field intensity shifts toward the upstream end of the channel. The potential drop and peak of the electron temperature for the 150th generation shift upstream compared those for the 50th generation. Consequently, the ionization region moves upstream as well (see figures 15 and 16), thereby further reducing the divergence angle. This observation aligns well with the prior findings [47‒49].
The optimal plume divergence angle is determined to be 41.27°, consistent with the experimentally determined angle for the designated magnetic field configuration. Through an extensive survey of literature concerning the SPT-70, the typical range of optimal plume divergence angles is revealed as 44.7°–57.4° [50‒55]. Specifically, Qian et al mentioned that the divergent angle of the plume of a stably operating SPT-70 model ranges from 40° to 60° [56]. These scholarly findings, while not identical, demonstrate a favorable comparison and serve to moderately validate the favorable qualities of our research outcomes.
The reproducibility of the genetic algorithm is tested by varying the crossover and mutation rates. Each parameter set was subjected to ten computational runs. A run was considered successfully converged, if the solution stabilized within 200 iterations and plume divergence angle was less than 42°. Conversely, slow convergence rates, oscillatory behavior, or convergence to a local rather than the global optimum indicated unsuccessful convergence. The reproducibility results are visually presented in figure 17. Satisfactory reproducibility was achieved at crossover rates between 0.26 and 0.38, and mutation rates between 0.012 and 0.021. Given the extensive computational demands, the number of runs was limited to ten per group to balance the tradeoff between algorithm performance and computational resources at our disposal.
As mentioned earlier, at the 50th generation, the genetic algorithm has already generated a magnetic field configuration with divergence. At the 150th generation, the magnetic field configuration has evolved into a magnetic field configuration with convergence. The comparison of the corrosion caused by plasma on the discharge channel wall at 100 h and 200 h of operation under the impact of these two types of magnetic field configurations is shown in figures 18 and 19.
The most pronounced corrosion occurs at the discharge channel’s outlet corner for both magnetic field configurations. After the outer corners of the ceramic wall are completely corroded, the magnetic pole coil will be completely exposed to plasma bombardment, causing sputtering corrosion. This will gradually cause the magnetic field configuration to deviate from the design conditions, and the performance of the thruster will deteriorate until it eventually reaching failure.
Both the results obtained from simulation and those from experiments suggest that the convergent magnetic field configuration can reduce the wall erosion more effectively than the divergent configuration, as shown in figures 18 and 19. The plasma corrosion on the inner and outer channel walls at the outlet angle, where the maximum corrosion depth exists, is reduced by 5.5% and 2.7%, respectively. The simulation results are slightly lower than the experimental results, verifying the reliability of the simulation model.
This study employs a genetic algorithm to iteratively optimize the magnetic field structure of Hall thrusters. Both the results obtained from simulation and those from experiments suggest that the algorithm significantly reduces the divergence angle of thruster plumes and reduces the corrosion of the discharge channel walls.
The optimization process of the genetic algorithm for magnetic fields is mainly divided into three steps. In the first step, the current intensities of both the internal and external excitation coils increase, and the maximum magnetic field intensity increases continually. After several generations of iterations, the plume quickly converges to a stable motion process. Due to the significant increase in the internal coil current which improves the overall performance at the first step, the inner coil current travels faster than the excitation current of the external coil. Therefore, we first noticed a divergent magnetic field structure in the thruster, manifested as the magnetic turning point located outside the centerline of channel [57]. In the second step, the current intensity of the inner coil gradually decreases, whereas the current intensity of the outer coil still increases. The magnetic field configuration gradually transitions to a convergent magnetic field configuration, and the plume’s divergence angle will decrease rapidly in the second stage. During the calculation process, it is also found that the ionization region at this stage moves upstream, which further reduces the divergence angle of the plume. The third step mainly manifests as adjustment of the excitation current of the internal trim coil, during which the divergence angle of the plume further decreases until it stabilizes.
Further studies on the corrosion of the discharge channels of the thruster after running for 100 h and 200 h indicated that the corrosion rates of the inner and outer channels were reduced by 5.5% and 2.7%, respectively. A wall corrosion model was employed for the simulations, whereas a laser shape instrument was employed for the experiment, and the two results achieved good consistency.
Overall, this study demonstrates that the iterative process of the genetic algorithm can be exploited in designing the magnetic field configuration for low- and medium-power Hall thrusters as SPT70. This study demonstrates the feasibility of using genetic algorithms to design magnetic fields through numerical simulations and experimental verifications. The genetic algorithm has also shown strong application prospects in addressing the magnetic field problems associated with high-power Hall thrusters and nested Hall thrusters.
This research was funded by Shanghai Natural Science Foundation (No. 12ZR1414700).
| [1] |
Bapat A, Salunkhe P B and Patil A V 2022 IEEE Trans. Plasma Sci. 50 189 doi: 10.1109/TPS.2022.3143032
|
| [2] |
Lev D et al 2019 Acta Astronaut. 159 213 doi: 10.1016/j.actaastro.2019.03.058
|
| [3] |
Ding Y J et al 2019 Rev. Mod. Plasma Phys. 3 15 doi: 10.1007/s41614-019-0036-y
|
| [4] |
Mazouffre S 2016 Plasma Sources Sci. Technol. 25 033002 doi: 10.1088/0963-0252/25/3/033002
|
| [5] |
Boeuf J P 2017 J. Appl. Phys. 121 011101 doi: 10.1063/1.4972269
|
| [6] |
Martinez-Sanchez M and Pollard J E 1998 J. Propul. Power 14 688 doi: 10.2514/2.5331
|
| [7] |
Linnell J A and Gallimore A D 2006 J. Propul. Power 22 1402 doi: 10.2514/1.19613
|
| [8] |
Ahedo E and Escobar D 2004 J. Appl. Phys. 96 983 doi: 10.1063/1.1759790
|
| [9] |
Andreussi T et al 2018 Plasma Phys. Control. Fusion 60 014015 doi: 10.1088/1361-6587/aa8c4d
|
| [10] |
Boyd I D 2001 J. Spacecr. Rockets 38 381 doi: 10.2514/2.3695
|
| [11] |
Taccogna F et al 2005 Phys. Plasmas 12 043502 doi: 10.1063/1.1862630
|
| [12] |
Haas J M and Gallimore A D 2001 Phys. Plasmas 8 652 doi: 10.1063/1.1338535
|
| [13] |
Hofer R R, Jankovsky R S and Gallimore A D 2006 J. Propul. Power 22 721 doi: 10.2514/1.15952
|
| [14] |
Wang C S et al 2011 Phys. Plasmas 18 013507 doi: 10.1063/1.3533915
|
| [15] |
Wei L Q et al 2009 Plasma Sources Sci. Technol. 18 045020 doi: 10.1088/0963-0252/18/4/045020
|
| [16] |
Wei L Q et al 2015 Chin. Phys. B 24 055201 doi: 10.1088/1674-1056/24/5/055201
|
| [17] |
Hara K, Keller S and Raitses Y Measurements and theory of driven breathing oscillations in a Hall effect thruster In: Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference Salt Lake City: AIAA 2016
|
| [18] |
Han L, Wei L Q and Yu D R 2016 J. Phys. D: Appl. Phys. 49 375203 doi: 10.1088/0022-3727/49/37/375203
|
| [19] |
Ma D et al 2020 Vacuum 180 109547 doi: 10.1016/j.vacuum.2020.109547
|
| [20] |
Gao Y Y et al 2016 Plasma Sources Sci. Technol. 25 035011 doi: 10.1088/0963-0252/25/3/035011
|
| [21] |
Hofer R R et al 2014 J. Appl. Phys. 115 043304 doi: 10.1063/1.4862314
|
| [22] |
Grimaud L and Mazouffre S 2017 J. Appl. Phys. 122 033305 doi: 10.1063/1.4995285
|
| [23] |
Ding Y J et al 2017 Jpn. J. Appl. Phys. 56 038001 doi: 10.7567/JJAP.56.038001
|
| [24] |
Yu D R et al 2009 Contrib. Plasma Phys. 49 413 doi: 10.1002/ctpp.200910038
|
| [25] |
Hallouin T and Mazouffre S 2020 Aerospace 7 58 doi: 10.3390/aerospace7050058
|
| [26] |
Hofer R R and Gallimore A D The role of magnetic field topography in improving the performance of a high voltage Hall thruster In: Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Indianapolis: AIAA 2002
|
| [27] |
Garrigues L et al 2003 Phys. Plasmas 10 4886 doi: 10.1063/1.1622670
|
| [28] |
Mazouffre S et al 2015 J. Propul. Power 31 1167 doi: 10.2514/1.B35417
|
| [29] |
Mirjalili S Genetic algorithm In: Mirjalili S Evolutionary Algorithms and Neural Networks: Theory and Applications Cham: Springer 2019: 43
|
| [30] |
Katoch S, Chauhan S S and Kumar V 2021 Multimed. Tools Appl. 80 8091 doi: 10.1007/s11042-020-10139-6
|
| [31] |
Popov G et al Electric propulsion subsystem development and application in Russia In: Proceedings of the 3rd International Conference Spacecraft Propulsion Cannes: European Space Agency 2000: 21
|
| [32] |
Haas J M et al 2000 Rev. Sci. Instrum. 71 4131 doi: 10.1063/1.1318921
|
| [33] |
Boyd I D 2006 IEEE Trans. Plasma Sci. 34 2140 doi: 10.1109/TPS.2006.879096
|
| [34] |
Brown N P and Walker M L R 2020 Appl. Sci. 10 3775 doi: 10.3390/app10113775
|
| [35] |
Ahedo E, Martínez-Cerezo P and Martínez-Sánchez M Model of plasma-wall interaction effects in a Hall thruster In: Proceedings of the 37th Joint Propulsion Conference and Exhibit Salt Lake City: AIAA 2001
|
| [36] |
Taccogna F and Garrigues L 2019 Rev. Mod. Plasma Phys. 3 12 doi: 10.1007/s41614-019-0033-1
|
| [37] |
Yan L et al 2012 J. Appl. Math. 2012 327021
|
| [38] |
Yim J, Keidar M and Boyd I An investigation of factors involved in Hall thruster wall erosion modeling In: Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Sacramento: AIAA 2006
|
| [39] |
Duan X Y et al 2020 J. Appl. Phys. 127 093301 doi: 10.1063/1.5140514
|
| [40] |
Reinke S, Kuhr M and Kulisch W 1995 Surf. Coat. Technol. 74‒75 723 doi: 10.1016/0257-8972(95)08271-9
|
| [41] |
Reinke S, Freudenstein R and Kulisch W 1997 Surf. Coat. Technol. 97 263 doi: 10.1016/S0257-8972(97)00219-3
|
| [42] |
Haldurai L, Madhubala T and Rajalakshmi R 2016 Int. J. Comput. Sci. Eng. 4 139
|
| [43] |
Manivannan S, Devi S P and Arumugam R Optimization of flat plate heat sink using genetic algorithm In: Proceedings of the 1st International Conference on Electrical Energy Systems Chennai: IEEE 2011: 78
|
| [44] |
Ding Y J et al 2019 J. Vac. Sci. Technol. B 37 012902 doi: 10.1116/1.5037440
|
| [45] |
Zhang Z et al 2018 Vacuum 155 199 doi: 10.1016/j.vacuum.2018.06.004
|
| [46] |
Ding Y J et al 2015 J. Propul. Technol. 36 795 (in Chinese)
|
| [47] |
Doh G et al 2021 J. Appl. Phys. 130 193301 doi: 10.1063/5.0066974
|
| [48] |
Shashkov A, Lovtsov A and Tomilin D 2019 Eur. Phys. J. D 73 173 doi: 10.1140/epjd/e2019-90641-y
|
| [49] |
Ning Z X et al 2011 Appl. Phys. Lett. 99 221502 doi: 10.1063/1.3665632
|
| [50] |
Kim V et al Plasma parameter distribution determination in SPT-70 plume In: Proceedings of the 28th International Electric Propulsion Conference Toulouse, France 2003
|
| [51] |
Fife J and Martinez-Sanchez M Characterization of the spt-70 plume using electrostatic probes In: Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit Cleveland: AIAA 1998
|
| [52] |
Sullivan R M 2010 The physics of high-velocity ions in the Hall thruster near-field PhD Thesis California Institute of Technology, Pasadena, USA
|
| [53] |
Leach R W 2012 Development of a Hall thruster test facility MSc Thesis Colorado State University, Fort Collins, USA
|
| [54] |
Dragnea H C et al 2015 IEEE Trans. Plasma Sci. 43 35 doi: 10.1109/TPS.2014.2320851
|
| [55] |
Marcovati A 2016 Z-70 hall thruster performance analysis. Experimental thrust and plasma measurements MSc Thesis School of Industrial and Information Engineering
|
| [56] |
Qian Z, Wang P and Du Z 2009 Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 223 115
|
| [57] |
Zhang G C et al 2022 Plasma Sources Sci. Technol. 31 095003 doi: 10.1088/1361-6595/ac89a8
|
| [1] | Liang HAN (韩亮), Jun GAO (高俊), Tao CHEN (陈涛), Yuntian CONG (丛云天), Zongliang LI (李宗良). A method to measure the in situ magnetic field in a Hall thruster based on the Faraday rotation effect[J]. Plasma Science and Technology, 2019, 21(8): 85502-085502. DOI: 10.1088/2058-6272/ab0f63 |
| [2] | Liuxiu HE (何柳秀), Minghai LIU (刘明海), Shuangyun ZHAO (赵双云). Spontaneous magnetic field multipolar structure in toroidal plasmas based on 2D equilibrium[J]. Plasma Science and Technology, 2019, 21(4): 45101-045101. DOI: 10.1088/2058-6272/aaf78d |
| [3] | Yafeng BAI (白亚锋), Shiyi ZHOU (周诗怡), Yushan ZENG (曾雨珊), Yihan LIANG (梁亦寒), Rong QI (齐荣), Wentao LI (李文涛), Ye TIAN(田野), Xiaoya LI (李晓亚), Jiansheng LIU (刘建胜). Optical measurements and analytical modeling of magnetic field generated in a dieletric target[J]. Plasma Science and Technology, 2018, 20(1): 14010-014010. DOI: 10.1088/2058-6272/aa8c6f |
| [4] | Abhishek GUPTA, Suhas S JOSHI. Modelling effect of magnetic field on material removal in dry electrical discharge machining[J]. Plasma Science and Technology, 2017, 19(2): 25505-025505. DOI: 10.1088/2058-6272/19/2/025505 |
| [5] | Y WANG (王宇), G ZHAO (赵高), C NIU (牛晨), Z W LIU (刘忠伟), J T OUYANG (欧阳吉庭), Q CHEN (陈强). Reversal of radial glow distribution in helicon plasma induced by reversed magnetic field[J]. Plasma Science and Technology, 2017, 19(2): 24003-024003. DOI: 10.1088/2058-6272/19/2/024003 |
| [6] | WU Ding (吴鼎), LIU Ping (刘平), SUN Liying (孙立影), HAI Ran (海然), DING Hongbin (丁洪斌). Influence of a Static Magnetic Field on Laser Induced Tungsten Plasma in Air[J]. Plasma Science and Technology, 2016, 18(4): 364-369. DOI: 10.1088/1009-0630/18/4/06 |
| [7] | LIU Huiping(刘惠平), ZOU Xiu(邹秀), QIU Minghui(邱明辉). Sheath Criterion for an Electronegative Plasma Sheath in an Oblique Magnetic Field[J]. Plasma Science and Technology, 2014, 16(7): 633-636. DOI: 10.1088/1009-0630/16/7/01 |
| [8] | XIA Zhiwei(夏志伟), LI Wei(李伟), LI Bo(李波), YANG Qingwei(杨青巍), LU Jie(卢杰). High Magnetic Field Shielding for Sensitive Devices Relevant to ITER[J]. Plasma Science and Technology, 2014, 16(6): 629-632. DOI: 10.1088/1009-0630/16/6/17 |
| [9] | WANG Changquan (王长全), ZHANG Guixin (张贵新), WANG Xinxin (王新新). Surface Treatment of Polypropylene Films Using Dielectric Barrier Discharge with Magnetic Field[J]. Plasma Science and Technology, 2012, 14(10): 891-896. DOI: 10.1088/1009-0630/14/10/07 |
| [10] | YUAN Zhongcai(袁忠才), SHI Jiaming (时家明), HUANG Yong (黄勇), XU Bo (许波). Faraday angle of Linearly Polarized Waves along Magnetic Field in Magnetized Collisional Plasmas[J]. Plasma Science and Technology, 2010, 12(5): 519-522. |
| Thruster type | Mass flow rate (mg/s) |
Rated power (W) |
Voltage (V) | Thrust (mN) | Specific impulse (s) |
| SPT70 | 2.6 | 650 | 300 | 40 | 1510 |